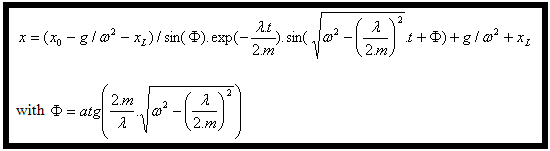设计过程中非常重要的一步是验证。若要验证设计,通常情况下,比较好的方法是使用简单可靠的理论实例来进行评估。下面就是这样的实例。
这些实例介绍了进行仿真输出验证的过程中使用的表达式和假设条件。
位移、质量弹簧实例
一种简单的质量和弹簧验证实例。

牛顿定律
![]() (1)
(1)
其中:
| 数值: | |
|---|---|
| |
|
| |
|
| |
|
| |
10 |
| |
20 |
| |
15000 |
| |
0.3 |
| |
9.81 |
| |
0.33 |
| |
0.0 |
|
(1) |
|
|
其中 |
|
|
|
|
|
此微分表达式的解答是: |
|
|
|
|
|
在系统平衡, |
|
|
结果 (2) |
|
|
|
|
|
|
|
|
初始条件为给定 A 值且 |
|
|
t = 0.0 时,(3) |
|
|
|
|
|
和 |
|
|
|
|
|
最后,(3) 中报告的 (4) 和 (6) 给出位移表达式: |
|
|
|
|
|
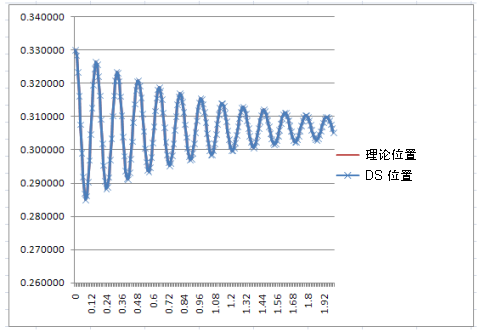
将在 Excel 中对此表达式进行编程,然后将结果与运动仿真生成的结果相比较,结果应该是完全相同的。 |
|
 |
|
位置和速度,曲柄活塞实例
此验证实例的目的是,检查运动仿真中输出的曲柄轴和活塞机构中的位置和速度,并将其与理论表达式进行比较看二者是否相同。
已知值:曲柄轴径与曲柄轴旋转中心之间的“行程”或距离,以及主承载轴径与活塞销连接之间连接杆的长度。
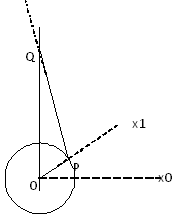
示意图
|
定义 |
R = 长度 (OP) = 曲柄轴投掷行程 L = 长度 (PQ) = 连接杆长度 |
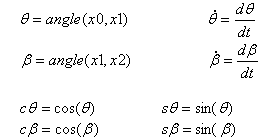 |
|
|
点 Q 相对于绝对坐标系 R0 的速度 = (x0, y0) |
|
|
|
// Q 在 R0 中的位置 |
|
|
// Q 在 R0 中的速度 |
| 其中:
|
|
| 且:
|
|
|
|
|
| 其中: |
|
| 且: |
|
| 结果: |
|
|
点 Q 位于 y0 轴上,x0 分量为 0.0: |
|
|
|
|
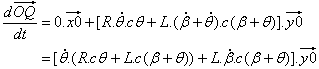 |
|
| 最后,使用 (1): | |
|
|
|
|
表达式 (1) 的结果是 |
|
|
(1) |
|
且 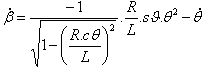 |
|
| 使用 MS Excel 和数值 (L=0.125m、R=0.06m 和 |
|
|
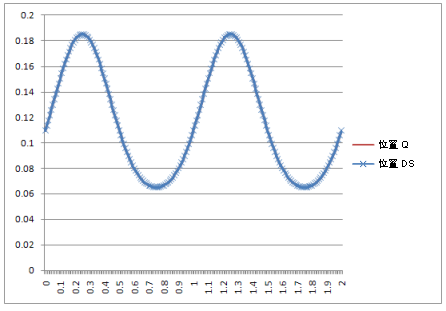
位置: |
|
 |
|
|
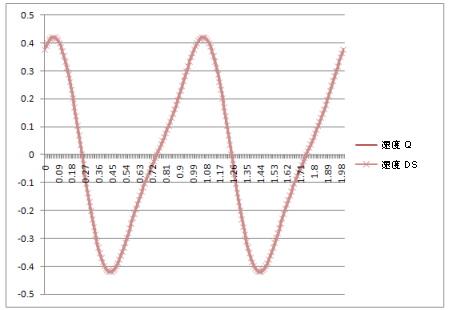
速度: |
|
 |
|
结果:动态仿真中的曲线与理论表达式中得到的那些曲线相同。
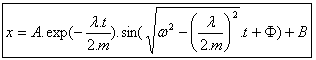 (3)
(3)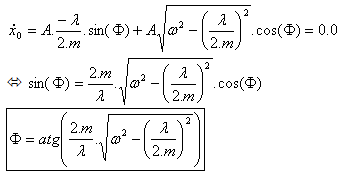 (5)
(5)