Moldflow 纤维取向模型基于 Folgar-Tucker 取向方程。
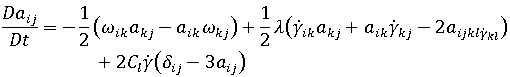
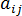是纤维取向张量。 
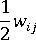是涡度张量， 
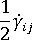是变形速率张量。 
是纤维相互作用系数，属于标量现象参数，其值通过拟合试验结果来确定。此术语被添加到初始 Jeffery 形式中，用来表示纤维与纤维的迭代。
）被引入模型：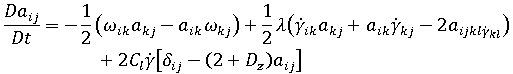 
以下是应用于修复模型的假设和注意事项：
-
Folgar-Tucker 模型给出了浓悬浮液中对纤维取向预测的可接受精确性。
-
使用混合闭合，因为其形式简单且具有良好的动态行为。
注意以下几点：
- 设置 = 0.0 将模型设置恢复为 Jeffery 模式。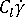
影响取向张量。如果 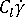= 0，纤维不发生相互作用；如果参数值 变得非常大，纤维排列的对齐度会随之下降。 - 术语 的大小设置了由于纤维相互作用，平面外方向上随机效应的强度。
- 设置 = 1.0 给出了 3D 问题的 Folgar-Tucker 取向模型。设置 = 0.0 给出了 2D 问题的 Folgar-Tucker 取向模型。
然而，注射成型模拟中，流动液体动力学会导致纤维主要位于流动平面上。它们的平面外旋转的性能会严重受限。这种机制预测了纤维取向在平面外方向的随机影响要远小于平面内方向，因此， 值较小。
- 降低此 参数：
- 减小平面外取向。
- 增大型芯层厚度。
- 模拟处理有关中性面对称的问题。
经验表达式 和缩放体积因子表达式
Bay 的实验工作建议将 Folgar 和 Tucker 相互作用的模型应用于注射成型问题。但是，如何才能知道应该在 纤维取向建模中应用哪个值呢？
采用 Folgar 和 Tucker 模型进行的试验结果表明 取决于纤维体积因子和纵横比，但依存度尚不清楚。
在薄膜浇口条中的流动主要是简单切变。外壳层（中性面覆盖 40-90% 的壁）应具有简单切变的平稳状态的值。这种情况下，将为检查此依据提供一个预备方法。
Bay 的外壳层取向结果显示，取向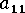 
对纤维浓度非常敏感，暗示可以建立起相互作用系数的经验关系。另外，Bay 的测量支持纤维扩散与应变率成比例的说法。
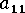Bay 的论文中给出了一些纤维细节上的相互作用系数依存度 的经验关系。该表达式是一个简单的指数 术语。数据来自不同材料 (PC、PBT、PA66) 的注射模具条的外壳层，每一种材料都具有 6-7 个玻璃液面。在浓度悬浮液中可能会考虑所有这些情况。
经修订的经验 表达式
根据外壳层取向结果，已对 玻璃内容范围中的 Bay 表达式中的默认值进行了审核。
在 = 1.0 （Folgar-Tucker 模型形式）的情况下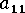， 意味着所有材料的全部玻璃内容的取向被过度预测。过度预测的等级随着玻璃内容的增加而降低。请参阅下图。
使用末端浇注条和中央浇注圆盘执行一系列纤维填充+保压分析检验过程。详细考虑了两种材料（PA66 和 PBT）的浇注条的外壳层取向 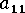和不同的玻璃等级，结果与 Bay 的试验取向数据相比较。取向等级通常为 0.8。
使用保压阶段的结果，得出经修订的经验表达式 和缩放体积因子 cL / d = 0.01 和 1.0。
更复杂的程序应用于中间 值。
下图显示了在这些情况中， 不同玻璃等级下，所有材料的外壳层 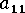取向预测中产生的错误：
- = 0（Jeffery 模型）。
- Bay 经验表达式 和 = 1.0（Folgar-Tucker 模型）。
- 对于典型的注塑模零件（零件厚度 < 2.5 mm），经修订的 模型具有较低的 值，例如 = 0.01 为默认值，如上所述，显示在下图中。
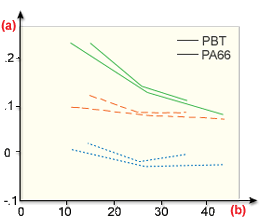
经修订的
. 模型具有较低的 值(a) 错误；(b) % 玻璃（权重）；
= 0.0（Jeffery 模型）；
Bay ( = 1.0)；
Moldflow 模型 (= 0.01） - 对于较厚的零件（厚度 > 2.5 mm），我们使用经修订的 模型，同时 = 1.0。其中 的值显示随着零件的厚度单调递增。增加的趋势与在平面外纤维取向随着零件厚度的增加而增加的期望一致。
可以进行以下观察：
- Jeffery 和 Folgar-Tucker 模型能导致取向评估中的过度预测。
- 低 模型实例导致较薄零件（厚度 < 2.5 mm）的错误级别大幅下降。
- 默认 Bay 模型的 值较低，提供的取向评估位于 Bay 试验数据的可信区间（只针对高玻璃级别而言）。
- 对于两种材料以及所有考虑在内的玻璃等级，已修复的模型显著提高了对其他模型情况的取向预测。
关于 概要− 组合
相互作用系数的有效数据范围， ，是 0-1.0；但我们发现，与试验结果相比，使用大于 0.1 的值并不能改善预测结果。
厚度力矩相互作用系数的有效数据范围， ，是 0.0001-1.0。
对适用于此软件版本的相互作用系数和厚度力矩组合在下表中进行了总结：
| 相互作用系数， |
相互作用系数的厚度力矩， |
注释 |
|---|---|---|
| 0 | 0.0001–1.0 |
|
| 0 < <= 0.1 |
1.0 | Folgar-Tucker 模型 |
| 默认 | <= 1.0，（默认 = 1.0） |
使用机械属性中的项和 ，根据缩放体积因子 (cL / d)，通过经验表达式得出
< 0.01 时基本不变 |
| 用户设置 (0–0.1) |
<= 1.0 （默认为 1.0） |
允许的其他实现 |
纤维取向的分析方案综述
在建模过程中，流体运动通过两种不同的方式控制点上的纤维取向：推导流动取向（运动期）和对流流动取向（对流期）。
对于运动期，预测精度取决于计算的速度梯度的精度。
对于对流期，预测精度取决于对取向梯度的计算。像速度一样，取向张量的表示也取决于坐标系。所有适合于速度梯度计算的数值方案可用于计算取向梯度。在纤维取向软件中，用同一单元系统表示速度和取向字段，从而用同一方案计算速度和取向梯度。
现在描述的是总体纤维取向方案的轮廓。纤维取向预测与模型填充模拟相结合。
首先，算法初始化计算填充和纤维取向。
然后，重复进行以下分析环节直到所有单元冻结为止：
- 确定填充 + 保压分析的时间段
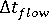。 - 提前流动前沿。
- 计算压力和速度字段以及应变张量。
- 计算对流期的稳定时间段
。 - 重复时间段直到
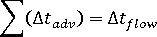。 - 对于每一单元中的每一栅格点：
- 计算对流纤维取向期直到
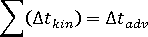为止。 - 计算运动纤维取向期。
- 计算运动期的时间段
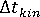。 - 在时间段 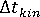计算新的纤维取向。
- 计算对流纤维取向期直到
- 返回到初始环节。