虽然遵循结构响应的完全非线性增量/迭代方法十分常见且相对来说比较精确,但它可能涉及大量的计算。
由于挫曲的基本重要性和设计关系,如果有一种简化方法可以逼近出现挫曲时对应的临界载荷级别,此方法无疑非常有用。因此,只要我们假设预挫曲响应是线性的且预挫曲位移的影响可忽略不计,便可以设计出这种方法。这种方法称为挫曲分析,也称为初始稳定性或经典分叉分析。
以下部分先后对广义挫曲分析方法及其采用的两种特定方法进行了介绍。
广义挫曲分析
挫曲分析的目的是确定施加载荷的一些已知分布 {P} 的 临界挫曲载荷。根据定义可以得出: 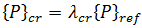 其中
其中
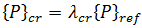
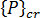 是施加载荷分布的临界级别,
是施加载荷分布的临界级别, 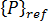 是同一载荷分布的任意级别(参考载荷),而
是同一载荷分布的任意级别(参考载荷),而 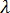 是标量乘数。
是标量乘数。
通过这些定义,载荷乘数 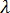 达到临界值时,便发生挫曲
达到临界值时,便发生挫曲 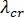 。挫曲分析的起点是假设刚度矩阵
。挫曲分析的起点是假设刚度矩阵 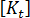 随施加载荷呈线性变化。如上所述,我们可以将施加载荷当作是某个参数(例如
随施加载荷呈线性变化。如上所述,我们可以将施加载荷当作是某个参数(例如 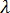 )乘以力的常向量
)乘以力的常向量 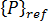 。
。
假设结构的两个已知状态(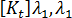 和
和 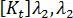 ),任何给定平衡配置对应的刚度矩阵,
),任何给定平衡配置对应的刚度矩阵, 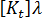 ,可表示为:
,可表示为: 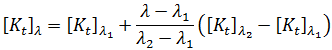
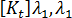 和
和 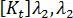 ),任何给定平衡配置对应的刚度矩阵,
),任何给定平衡配置对应的刚度矩阵, 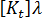 ,可表示为:
,可表示为: 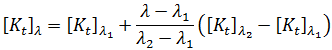
如果将分数项定义为 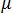 ,将从
,将从 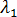 到
到 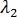 的硬度变化定义为
的硬度变化定义为 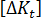 ,然后执行下列操作:
,然后执行下列操作: 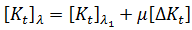 挫曲点有两种平衡配置, {U} 和
挫曲点有两种平衡配置, {U} 和 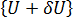 ,二者处于相同的载荷级别。
,二者处于相同的载荷级别。
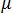 ,将从
,将从 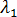 到
到 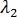 的硬度变化定义为
的硬度变化定义为 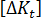 ,然后执行下列操作:
,然后执行下列操作: 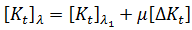
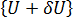 ,二者处于相同的载荷级别。
,二者处于相同的载荷级别。 下图即对此进行了说明,该图显示了两种基本挫曲类型的平衡配置(稍后将做详细介绍)。
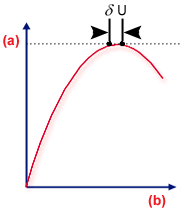
极限点
.(a) 载荷,(b) 变形
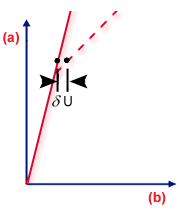
分叉点
.(a) 载荷,(b) 变形
使用线性分析的基本方程 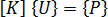 ,由此可得出:
,由此可得出: 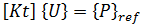
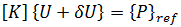 其中 {U} 是对应载荷 {P] 的位移,然后
其中 {U} 是对应载荷 {P] 的位移,然后 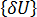 表示两个平衡配置间的无穷小位移。用第二个方程减去第一个方程得出:
表示两个平衡配置间的无穷小位移。用第二个方程减去第一个方程得出: 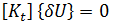 其中
其中 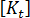 为
为 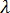 的函数。通过线性代数我们知道求解上述方程相当于求解:
的函数。通过线性代数我们知道求解上述方程相当于求解: 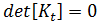 因而,当
因而,当 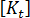 的行列式为零时,将发生挫曲。因此,针对广义挫曲问题要求解的方程式为: 这是特征问题,其中 是要求解的未知数。可以采用标准方法(例如子空间迭代)求解上述方程。
的行列式为零时,将发生挫曲。因此,针对广义挫曲问题要求解的方程式为: 这是特征问题,其中 是要求解的未知数。可以采用标准方法(例如子空间迭代)求解上述方程。
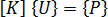 ,由此可得出:
,由此可得出: 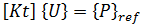
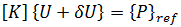
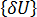 表示两个平衡配置间的无穷小位移。用第二个方程减去第一个方程得出:
表示两个平衡配置间的无穷小位移。用第二个方程减去第一个方程得出: 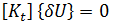
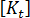 为
为 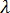 的函数。通过线性代数我们知道求解上述方程相当于求解:
的函数。通过线性代数我们知道求解上述方程相当于求解: 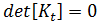
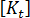 的行列式为零时,将发生挫曲。因此,针对广义挫曲问题要求解的方程式为: 这是特征问题,其中 是要求解的未知数。可以采用标准方法(例如子空间迭代)求解上述方程。
的行列式为零时,将发生挫曲。因此,针对广义挫曲问题要求解的方程式为: 这是特征问题,其中 是要求解的未知数。可以采用标准方法(例如子空间迭代)求解上述方程。 通过重新排列 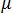 的定义,得出:
的定义,得出: 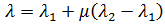 由此得出引起挫曲所需的载荷乘数。该分析采用此通用方法的两种简化形式,分别称为“线性(经典)挫曲分析”和“线性化挫曲分析”。
由此得出引起挫曲所需的载荷乘数。该分析采用此通用方法的两种简化形式,分别称为“线性(经典)挫曲分析”和“线性化挫曲分析”。
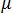 的定义,得出:
的定义,得出: 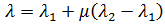
线性(经典)挫曲分析
在此方法中,我们选择 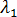 = 0,
= 0, 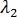 = 1,即将零和全部施加载荷作为参考状态。这种情况下
= 1,即将零和全部施加载荷作为参考状态。这种情况下 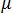 减小为
减小为 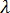 ,因而方程变为:
,因而方程变为: 
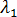 = 0,
= 0, 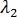 = 1,即将零和全部施加载荷作为参考状态。这种情况下
= 1,即将零和全部施加载荷作为参考状态。这种情况下 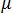 减小为
减小为 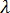 ,因而方程变为:
,因而方程变为: 
更新的拉格朗日理论可用于将 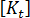 分为两个组成部分:
分为两个组成部分: 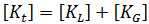 其中
其中 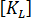 为一阶刚度矩阵,
为一阶刚度矩阵, 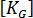 是更高阶刚度矩阵(也称为应力矩阵或几何矩阵)。
是更高阶刚度矩阵(也称为应力矩阵或几何矩阵)。 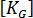 是材料应力的线性函数。
是材料应力的线性函数。 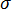 。
。
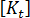 分为两个组成部分:
分为两个组成部分: 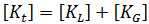
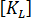 为一阶刚度矩阵,
为一阶刚度矩阵, 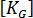 是更高阶刚度矩阵(也称为应力矩阵或几何矩阵)。
是更高阶刚度矩阵(也称为应力矩阵或几何矩阵)。 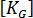 是材料应力的线性函数。
是材料应力的线性函数。 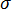 。
。 如果零件开始时未受到应力,则 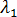 = 0 表示
= 0 表示 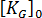 = 0。因而:
= 0。因而: 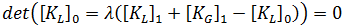
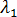 = 0 表示
= 0 表示 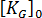 = 0。因而:
= 0。因而: 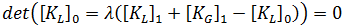
经典方法中做出的关键假设是高达 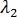 = 1 时对应的响应是完全线性的,即 使用原始坐标求解应力
= 1 时对应的响应是完全线性的,即 使用原始坐标求解应力 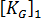 。经典方法中做出的另一个假设是刚度的一阶部分不随载荷变化,即
。经典方法中做出的另一个假设是刚度的一阶部分不随载荷变化,即 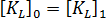 。在整个的拉格朗日术语中,这相当于忽视所谓的“位移矩阵”影响。“”因此,上述方程简化为:
。在整个的拉格朗日术语中,这相当于忽视所谓的“位移矩阵”影响。“”因此,上述方程简化为: 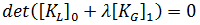
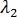 = 1 时对应的响应是完全线性的,即 使用原始坐标求解应力
= 1 时对应的响应是完全线性的,即 使用原始坐标求解应力 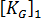 。经典方法中做出的另一个假设是刚度的一阶部分不随载荷变化,即
。经典方法中做出的另一个假设是刚度的一阶部分不随载荷变化,即 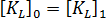 。在整个的拉格朗日术语中,这相当于忽视所谓的“位移矩阵”影响。“”因此,上述方程简化为:
。在整个的拉格朗日术语中,这相当于忽视所谓的“位移矩阵”影响。“”因此,上述方程简化为: 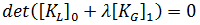
线性挫曲方法适用于不基于翘曲初始条件的结构分析或翘曲分析。实践证明对翘曲问题使用经典挫曲分析可准确预测挫曲载荷。经典方法之所以适用,是因为挫曲前形状变化极小,即 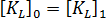 非常逼近。
非常逼近。
线性化的挫曲分析
在此方法中,我们选择 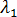 = 0,
= 0, 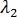 非常接近
非常接近 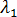 ,即将零和极小部分载荷作为参考状态。由于只采用很小的步,因此不需要平衡迭代,分析将利用策略 5 执行此步。
,即将零和极小部分载荷作为参考状态。由于只采用很小的步,因此不需要平衡迭代,分析将利用策略 5 执行此步。
另外假设 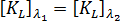 。请注意,此方法将使用更新后的坐标求解应力。
。请注意,此方法将使用更新后的坐标求解应力。
这时方程为: 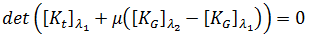
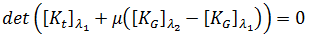
分析预应力部分的最简单快速方法是使 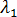 = 0,
= 0, 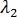 = 0.001。因而只需要采取一步,而且因为没有使用平衡迭代,求解时间只比经典方法的求解时间略长一些。
= 0.001。因而只需要采取一步,而且因为没有使用平衡迭代,求解时间只比经典方法的求解时间略长一些。
线性化挫曲方法专用于基于翘曲分析初始条件的结构分析。不能对这些问题采用经典方法,因为处理过程会产生大量残余应力。此违反假设 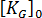 = 0。因而必须使用线性化的挫曲方法代替。选择初始条件挫曲分析时,应力将指示此点。
= 0。因而必须使用线性化的挫曲方法代替。选择初始条件挫曲分析时,应力将指示此点。