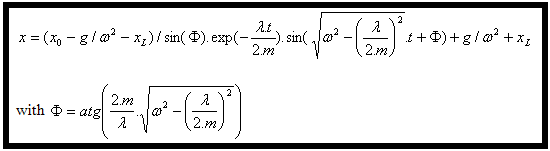在重要的設計過程中,驗證是其中的一個步驟。為了驗證設計,使用簡單可靠的理論實例來進行測試通常是不錯的方法。以下即為此類實例。
這些實例描述了用於完成驗證模擬輸出的方程式和假設。
位移,質量-彈簧實例
簡單的質量和彈簧驗證實例。

牛頓定律:
![]() (1)
(1)
其中:
| 數值: | |
|---|---|
| |
|
| |
|
| |
|
| |
10 |
| |
20 |
| |
15000 |
| |
0.3 |
| |
9.81 |
| |
0.33 |
| |
0.0 |
|
(1) |
|
|
其中: |
|
|
|
|
|
此微分方程式的解為: |
|
|
|
|
|
系統穩定 ( |
|
|
然後,(2) |
|
|
|
|
|
|
|
|
初始條件提供 A 值以及 |
|
|
對於 t = 0.0,(3) |
|
|
|
|
|
與 |
|
|
|
|
|
最後,(3) 中記錄的 (4) 和 (6) 提供位移的方程式: |
|
|
|
|
|
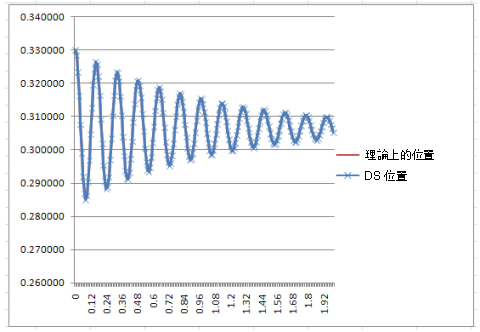
然後,將此方程式編入 Excel 中,將其結果與動力學模擬產生的結果進行比較,結果是相同的。 |
|
 |
|
位置和速度,曲柄-活塞實例
此驗證實例的目的是,當動力學模擬的輸出與理論方程式描述的相同時,檢查機軸和活塞機構中的位置和速度。
已知值:機軸軸頸距機軸旋轉中心的「投距」或距離、主軸承旋轉和活塞銷接頭之間的連接桿長度。
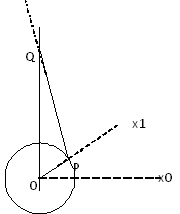
圖
|
定義 |
R = 長度(OP) = 旋轉投距 L = 長度(PQ) = 連接桿長度 |
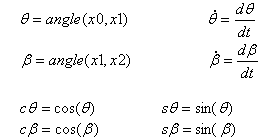 |
|
|
點 Q 相對於絕對座標系統的速度 R0 = (x0, y0) |
|
|
|
// R0 中點 Q 的位置 |
|
|
// R0 中點 Q 的速度 |
| 其中:
|
|
| 和:
|
|
|
|
|
| 其中: |
|
| 和: |
|
| 然後: |
|
|
點 Q 在 y0 軸線上,x0 分量是 0.0: |
|
|
|
|
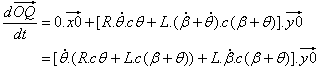 |
|
| 最後,使用 (1): | |
|
|
|
|
方程式 (1) 得出 |
|
|
(1) |
|
與 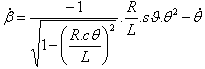 |
|
| 使用 MS Excel 和數值 (L=0.125m,R=0.06m 和 |
|
|
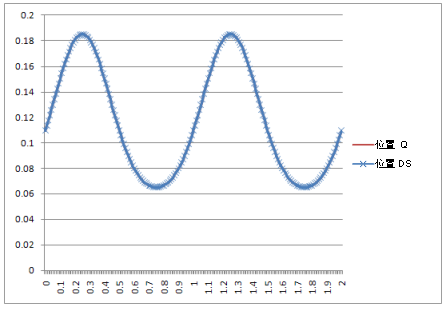
位置: |
|
 |
|
|
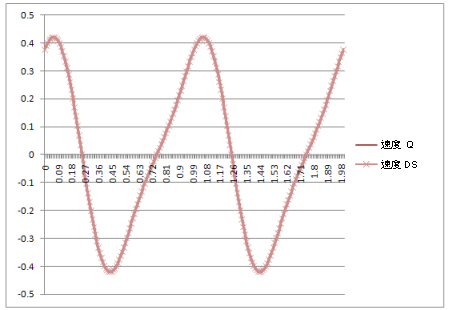
速度: |
|
 |
|
結果:動力學模擬中的曲線與理論方程式產生的曲線相同。
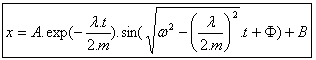 (3)
(3)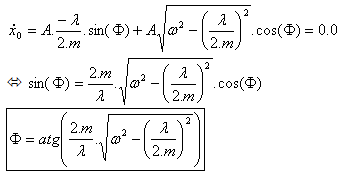 (5)
(5)