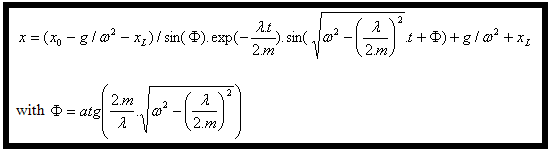Jedním z kroků zodpovědného přístupu k procesu návrhu je ověření. K ověření návrhu je často vhodné použít jednoduché spolehlivé teoretické případy, které poslouží jako vzory. Následující případy jsou právě takové.
V těchto případech jsou popsány výrazy a předpoklady používané k ověření výstupních hodnot simulace.
Posunutí, případ hmotnosti a pružiny
Případ jednoduchého ověření hmotnosti a pružiny.

Newtonův zákon:
![]() (1)
(1)
S výrazy:
| Číselná hodnota: | |
|---|---|
| |
|
| |
|
| |
|
| |
10 |
| |
20 |
| |
15 000 |
| |
0,3 |
| |
9,81 |
| |
0,33 |
| |
0,0 |
|
(1) |
|
|
s |
|
|
|
|
|
Řešením této diferenciální rovnice je: |
|
|
|
|
|
Konkrétní řešení, jestliže je systém stabilizovaný, je pro |
|
|
Pak (2) |
|
|
|
|
|
|
|
|
Z počátečních podmínek vyplývá hodnota a a |
|
|
pro t = 0,0, (3) |
|
|
|
|
|
a |
|
|
|
|
|
Nakonec (4) a (6) uvedené v (3) udává rovnici posunutí: |
|
|
|
|
|
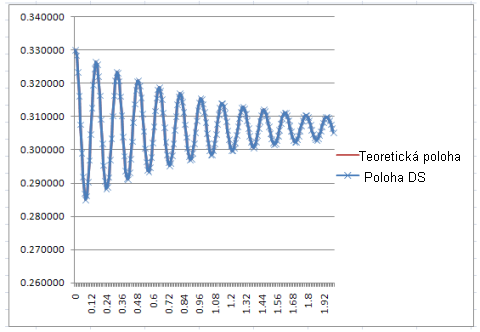
Rovnice pak byla naprogramována v aplikaci Excel a výsledky byly porovnány s výsledky získanými dynamickou simulací. Výsledky byly totožné. |
|
 |
|
Poloha a rychlost, případ kliky a pístu
Cílem tohoto případu ověření je kontrola polohy a rychlosti v mechanismu s klikovým hřídelem a pístem, kdy je výstup dynamické simulace a teoretické rovnice popisují totéž.
Známé hodnoty: Zdvih neboli vzdálenost otočného čepu klikového hřídele od středu otáčení klikového hřídele a délka ojnice mezi osou hlavního ložiska a kolíkovým spojem pístu.
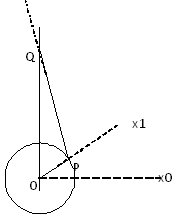
Diagram
|
Definice |
R = délka(OP) = zdvih klikového hřídele L = délka(PQ) = délka ojnice |
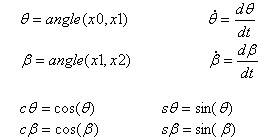 |
|
|
Rychlost bodu Q vzhledem k absolutnímu souřadnicovému systému R0 = (x0, y0) |
|
|
|
// poloha Q v R0 |
|
|
//rychlost Q v R0 |
| s:
|
|
| a:
|
|
|
|
|
| s: |
|
| a; |
|
| pak: |
|
|
Bod Q zůstává na ose y0 a složka x0 se rovná 0,0: |
|
|
|
|
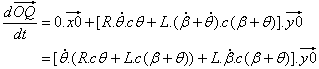 |
|
| Nakonec pomocí (1): | |
|
|
|
|
Výsledkem rovnice (1) je |
|
|
(1) |
|
a 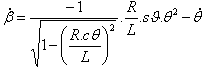 |
|
| Pomocí aplikace Microsoft Excel a číselných hodnot (L=0,125m, R=0,06m a |
|
|
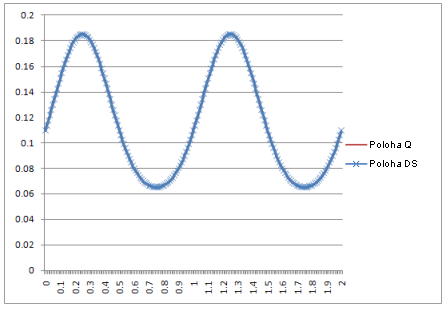
Poloha: |
|
 |
|
|
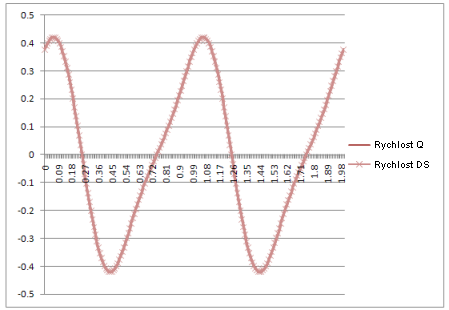
Rychlost: |
|
 |
|
Výsledek: křivky v dynamické simulaci jsou totožné s křivkami vytvořenými pomocí teoretických rovnic.
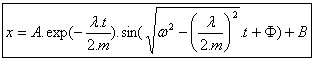 (3)
(3)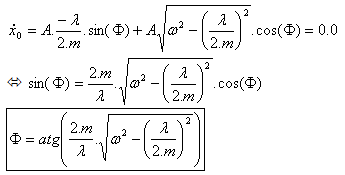 (5)
(5)