Kritische Knicklast

Bei der Analyse der kritischen Knicklast (auch als Eigenwert-Knickanalyse bezeichnet) wird die geometrische Stabilität von Modellen unter überwiegend axialen Lasten untersucht. Knicke können bei den meisten Produkten verheerende Folgen haben, wenn sie im normalen Gebrauch auftreten. Sobald die Geometrie beginnt, sich zu verformen, kann sie nicht einmal mehr dem Bruchteil der anfänglich angewendeten Kraft widerstehen.

Die für die kritische Knicklast verfügbaren Elementtypen sind Balken, Schalen und Ziegel (und ihre Varianten). Das ausgewählte Element kann sich auf den Typ des berechneten Knickfaktor auswirken. So sind z. B. Balkenelemente nur eine Linie, wobei der Querschnitt mathematisch dargestellt wird; Balken können nur ein globales Ausknicken berechnen. Schalen- und Ziegelelemente können lokales Ausknicken berechnen, da der Querschnitt mit Elementen modelliert wird. Siehe Abbildung 1.


(a) Balkenelemente erzeugen eine globale Ausknickungsform und einen lokalen Lastmultiplikator.
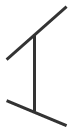	Querschnitt
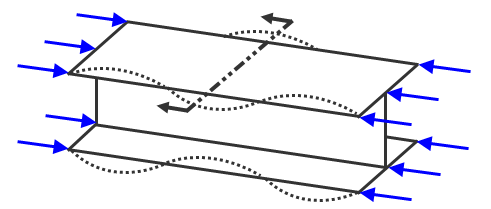
(b) Schalen- und Ziegelelemente können globale und lokale Auswirkungen erzeugen. In diesem Beispiel wird der Flansch des Balkens lokal ausgeknickt, was bei einer kritischen Last geschehen kann, die kleiner ist als die Last, die ein globales Ausknicken verursacht.
Abbildung 1: Exzentrische Last auf Säule oder Stange

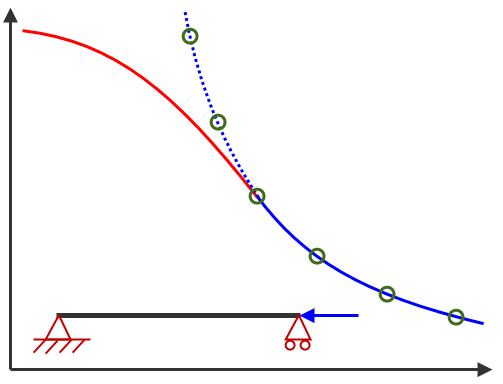
Da die kritische Knicklast berechnet wird, indem ein Eigenwert-Problem gelöst wird (wie bei einer Modalanalyse), sind die Ergebnisse für dünne und schmale Bauwerke geeignet (z. B. Euler-Stäbe). Es sind keine Korrekturen für kurze Säulen, dicke Schalen (verglichen mit der Länge und Breite der Schale) oder die Streckfestigkeit des Materials enthalten. Siehe Abbildung 2. Zudem handelt es sich um eine lineare Analyse. Es gibt keine Steifigkeitsänderungen aufgrund von Verformungen, und somit keine großen Verformungseffekte wie z. B. P-Delta-Effekte (Lastverformung). Somit können die kritische Last und die Knickmodusform bestimmt werden, was jedoch nach dem Ausknicken geschieht, ist nicht verfügbar. (Führen Sie eine nichtlineare Analyse durch, wenn Ergebnisse nach dem Ausknicken benötigt werden.)

Kritische Last

Euler-Gleichung Johnson-Korrektur berechnete Ergebnisse	Schlankheitsverhältnis
Abbildung 2: Exzentrische Last auf Säule oder Stange

Mithilfe der Knickanalyse können Sie ermitteln, ob bestimmte Lasten ein Ausknicken verursachen, und die Form des Knickmodus bestimmen. Dann können Sie Stützen oder Steifen entwerfen, um lokale Knicke zu verhindern. Dies ist in Situationen hilfreich, in denen ein Bauteil oder eine Baugruppe einer Axiallast ausgesetzt ist, oder wenn in einem Modell eine Kantenstauchung stattfindet.

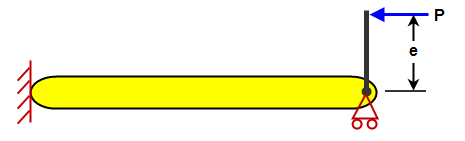
Lasten, die keine Stauchung verursachen, wirken sich nicht auf die Knickberechnung aus. Es ist unbedingt zu beachten, dass bei der Berechnung der kritischen Knicklast für Balkenelemente nur die axiale Komponente der Lasten berücksichtigt wird. Stellen Sie sich z. B. eine Versatzlast am Ende einer Stange vor (siehe Abbildung 3 (a)). Sie kann als Axiallast und -moment am Ende eines Balkenmodells dargestellt werden (Abbildung 3 (b)). Da das Moment keine axiale Spannung in den Balkenelementen erzeugt, führt die Versatzlast in dieser Analyse zu demselben Ergebnis wie eine reine Axiallast. (Das Moment erzeugt Biegespannungen; die theoretische Stauchung auf einer Seite des Balkenelements wirkt sich nicht auf die Knickberechnung aus.)

(a) Physisches Modell einer Stange mit einer Last P, die um einen Abstand e von der Mittellinie versetzt ist.

(b) In FEM erstelltes Balkenmodell. Die Lastexzentrizität hat zur Folge, dass ein Moment auf den Knoten angewendet wird. Aufgrund der Beschaffenheit von Balkenelementen und der kritischen Knicklast wirkt sich das Moment nicht auf die Ergebnisse aus. In diesem Beispiel wird der falsche Elementtyp verwendet.

Abbildung 3: Exzentrische Last auf Säule oder Stange

Die berechneten Knicklastfaktoren werden in der Ergebnisanzeige, in der Protokolldatei und in der Übersichtsdatei angezeigt. Der Knicklastfaktor gibt an, wann das Modell ausknickt. Multiplizieren Sie alle auf das Modell angewendeten Lasten mit dem Knicklastfaktor, und Sie erhalten die theoretische Last, die ein Ausknicken bewirkt. Aufgrund von Fehlern bei der realen Herstellung (ursprüngliche Krümmung, exentrische angewendete Lasten usw.) neigen echte Bauteile dazu, bei geringeren Lasten als dem theoretischen Wert auszuknicken. Kleine Abweichungen können in der Realität enorme Auswirkungen auf die kritische Last haben.

Wenn der Knicklastfaktor negativ ist, bedeutet dies, dass die Umkehrung der angewendeten Lasten (und ein Skalieren mit dem Faktor) zu einem Ausknicken des Modells führt. Angenommen, auf das Modell wird ein Druck von 1000 Pa ausgeübt. Der Druck versetzt es jedoch unter Spannung. Ein Knickfaktor von -0,75 gibt an, dass das Bauteil bei einer Druckbelastung von 750-Pa ausknickt.

Einschließen konstanter Lasten

Beim kritischen Knicken werden alle angewendeten Lasten mit dem berechneten Knickfaktor skaliert. In manchen Situationen kann es sinnvoll sein, die veränderlichen Lasten (z. B. Druck) zu skalieren, während andere Lasten (z. B. die Schwerkraft) nicht skaliert werden. Gehen Sie wie folgt vor, wenn die konstanten Lasten von Bedeutung sind und berücksichtigt werden müssen.

Schätzen Sie entweder durch Erfahrung, per Handrechnung oder durch Durchführen der Analyse, wie hoch der Knickfaktor voraussichtlich ausfallen wird. Nennen Sie ihn den letzten Knickfaktor.
Ändern Sie die konstanten Lasten in die Menge (konstante Last/letzter Knickfaktor), und belassen Sie die veränderlichen Lasten bei dem angegebenen Wert.
Führen Sie die Knickanalyse durch.
Wenn sich aus der neuen Knickberechnung derselbe Knickfaktor ergibt, ist die Lösung in Ordnung,. Die konstanten Lasten des Knickergebnisses entsprechen (konstante Last/letzter Knickfaktor) * (neuer Knickfaktor) = konstante Last, und die veränderliche Last, die ein Knicken verursacht, entspricht (variable Last) * (neuer Knickfaktor).
Wenn sich aus der neuen Knickberechnung ein anderer Knickfaktor ergibt, ersetzen Sie den letzten Knickfaktor durch den neuen Wert. Wiederholen Sie Schritt 2 bis 5.

Da es sich beim kritischen Knicken um eine Eigenwert-Lösung handelt, stellen die Verschiebungsergebnisse die Form des Knickmodus dar. Das Ausmaß der Verschiebungen ist nicht von Bedeutung. Gleichermaßen können einer Analyse der kritischen Knicklast keine Spannungs- oder Dehnungsergebnisse entnommen werden.