Ein deutscher Ingenieur, Albert, führte Anfang des 19. Jahrhunderts die ersten bekannten Untersuchungen zur Ermüdungsgrenze durch. Es wurde verstanden, dass ein Material, das immer wiederkehrender Belastung ausgesetzt ist, schließlich ausfällt. Es waren jedoch die um sich greifenden Ausfälle von Eisenbahnwaggon-Achsen nach vielen Meilen von offensichtlich fehlerfreiem Service, welche begannen, die Aufmerksamkeit auf das Phänomen zu lenken, das später als Ermüdung bekannt wurde.
Auf die meisten Konstruktionskomponenten und Strukturen wird eine Art zyklische Belastung ausgeübt. Fehler in solchen Komponenten bedeuten in der Regel den Anfang kleiner Risse, die sich später verbinden, um große Risse und katastrophale Ausfälle zu verursachen. Die ersten Risse beginnen bei Spannungen unterhalb der monotonen Streckgrenze des Materials. Im Laufe der Zeit häufen sich die (wiederholten) Schäden an, bis es schließlich zum Ausfall kommt. Es wurde häufig berichtet, dass über 90% der Strukturfehler als Ergebnis von Ermüdungsschäden auftreten.
Zwei grundlegende Methoden stehen zur Verfügung, um die Anzahl der Wiederholungen für eine zyklische Last festzustellen, die ein Material oder eine Komponente aushalten kann.
Die ersten Verfahren verwendeten Materialdaten, die zuerst im 19. Jahrhundert von Wholer gesammelt wurden. Dieses Verfahren bezog die Spannung in einer Komponente auf eine empirische Kurve, die sogenannte S-N Kurve (oder Wholer-Linie), um eine Schätzung der Anzahl der Zyklen bis zum Ausfall zu erhalten. Diese Technik wird weiterhin verwendet und wird normalerweise als Spannungs-Lebensdauer bezeichnet. Diese Methode verwendet die Komponentenspannung und geht davon aus, dass die Spannung im elastischen Bereich des Materials bleibt. Deshalb ist es am besten für Ermüdungsbruch geeignet, wo 100000+ Zyklen bis zum Ausfall erforderlich sind.
Das zweite und modernere Verfahren verwendet die Materialdehnung zur Vorhersage des Ausfalls. Kurven, die Dehnung in bezug zu Zyklen setzen, können aus Tests oder empirischen Formeln vorbereitet werden, ähnlich wie die für die Spannungs-Lebensdauer. Der große Vorteil bei der Verwendung dieses Verfahrens ist, dass die Dehnungs-Lebensdauer-Kurve den lokalen Dehnungsstatus der Komponente darstellt und die lokale plastische Verformung angeben kann. Dadurch verbessert sich die Genauigkeit der Lebensdauerprognose bei Lasten, wenn lokale Streckung auftritt, erheblich.
Der Assistent für die Ermüdungsberechnung verwendet beide Methoden, um die Gebrauchsermüdung vorherzusagen.
Definition der Belastung
Ermüdungsschäden werden durch die Belastung einer Struktur mit sich wiederholenden Belastungen über einen Zeitraum verursacht. Um Ermüdungsbruch zu analysieren, ist es erforderlich, die angewendete Last zu definieren. Im Assistent für die Ermüdungsberechnung können Sie zwei grundlegende Lasttypen definieren, die einfachste Form ist die konstante Amplitude harmonisch.
Die Belastung wird vollständig durch die Definition einer Spannungsmplitude SA und einer mittlere Spannung SM beschrieben. Der sich wiederholende Zyklus ist ein einzelner harmonischer Zeitraum, Punkte 1-2-3-4 in Abbildung 1.
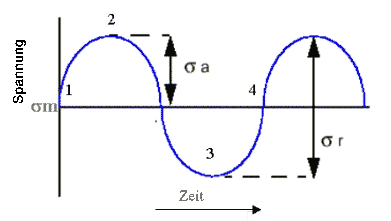
Abbildung 1 Konstante Amplitudenbelastung harmonisch
Die zweite Art der Belastung, und allgemeinerer Fall, ist die variable Amplitudenlast.
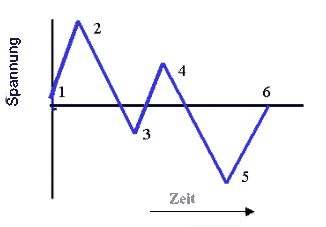
Abbildung 2 Variable Amplitudenbelastung
Variable Amplitudenbelastung besteht aus vielen einzelnen konstanten Amplitudenzyklen. Diese einzelnen Zyklen können unterschiedliche Amplituden und Mittelwerte haben und können überlagernd oder nachfolgend sein. Abbildung 2 zeigt ein einfaches Beispiel für eine variable Amplitudenbelastung. Wie Sie sehen, gibt es zwei einfache Zyklen: 1-2-5-6 bildet einen einzelnen Zyklus mit großer Amplitude, auf dem der kleinere Zyklus 3-4-3 überlagert wird. Eine variable Amplitudenbelastung kann daher in eine Anzahl einfacherer konstanter Amplitudenbelastungen untergeteilt werden. Dann werden sie in der Ermüdungsanalyse verwendet, um Schäden vorherzusagen.
Wenn eine variable Amplitudenbelastung für die Ermüdungsberechnung angewendet werden soll, muss eine Methode zum Extrahieren der 'Unterzyklen' angewendet werden. Der Assistent für die Ermüdungsberechnung wendet sie durch einen standardmäßigen Rainflow-Zählungs-Algorithmus an.
Rainflow-Zählung und Ermüdungsschäden
Sowohl die Spannungs-Lebensdauer- als auch die Dehnungs-Lebensdauer-Techniken der Ermüdungsbruchprognosen basieren auf einer einzelnen Zyklusschadenskurve. Diese Schadenskurve bringt die Anzahl der Wiederholungen mit der Spannungs- oder Dehnungsamplitude für einen einfachen Zyklus in Zusammenhang. Diese Kurve kann direkt verwendet werden, wenn die strukturelle Belastung der einfache konstante Amplitudentyp ist. Wenn jedoch eine variable Amplitudenbelastung definiert ist, müssen einige Schritte zum Berechnen der Lebensdauer mit der angewendeten Last ausgeführt werden.
Zuerst wird die Schwankungsbreite des Belastungsverlaufs ausgewählt. Dieser Vorgang durchsucht den Zeitverlauf für alle Punkte, die keine 'Umkehrungspunkte' sind, und verwirft sie, um unnötige Daten zu reduzieren. Nun wird der reduzierte Zeitverlauf mit einem standardmäßigen Rainflow-Zählungs-Algorithmu verarbeitet, der einzelne einfache Zyklen extrahiert. Diese einfachen Zyklen werden dann mit den einzelnen Zyklusschadenskurven zur Berechnung der Lebensdauer für jede Zyklus verwendet.
Nachdem Sie eine Lebensdauer für jeden einzelnen Zyklus im Zeitverlauf berechnet haben, wird eine Methode zur Bestimmung des kumulative Schadens oder der gesamten Lebensdauer erforderlich. Der Assistent für die Ermüdungsberechnung verwendet die ausführlich dokumentierte 'Miner-Regel'. Diese Regel besagt, dass der gesamte über einen Belastungsverlauf akkumulierte Schaden die lineare Summe der Schäden aus den einzelnen Zyklen ist.
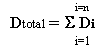
oder
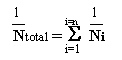
Dabei gilt: N ist die Lebensdauer in Wiederholungen und D ist der Schaden.
Spannungs-Lebensdauer-Technik
Die Spannungs-Lebensdauer-Methode verwendet eine einzelne Zyklusschadenskurve, bezeichent als SN-Kurve. Diese Kurve setzt die Spannungsamplitude im Verhältnis zur Anzahl der Zyklen und zu den Ausfällen. Da diese Methode seit mehreren Jahren weit verbreitet ist, sind Kurven und Materialdaten mit Bezug auf solche Kurven sofort verfügbar. Der für die Kurve verwendete Spannung hängt von den Daten in der Kurve und in einem gewissen Maße vom Ermessen des Ingenieurs ab. Die uniaxiale Version des Assistenten für die Ermüdungsberechnung verwendet die 'schlechteste absolute Hauptspannung' in den Berechnungen, da die Richtung der Spannungen als konstant angenommen wird.
Der Assistent für die Ermüdungsberechnung erzeugt die SN-Kurve intern aus den vom Ingenieur eingegebenen Materialdaten. Erforderliche Daten sind die monotone Zugfestigkeit des Materials und eine 'Ermüdungsgrenze'.
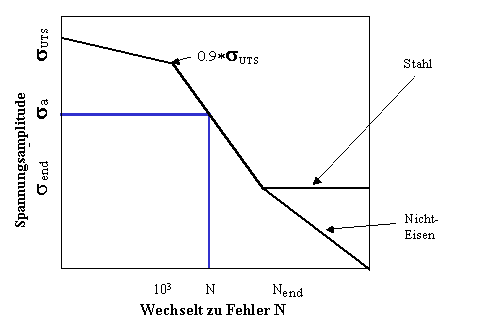
Abbildung 3 SN-Kurve
Die SN-Kurve hat die Form wie in Abbildung 3. SN-Kurven werden immer auf einer doppelt-logarithmischen Skala geplottet, wie in der Abbildung gezeigt. Die Kurve startet aus der monotonen Zugfestigkeit 'suts' bei log(N)=1. Es erreicht dann ungefähr den Bereich bis zu einem Wert von 1000 Zyklen durch eine gerade Linie mit einem Wert von 90% von 'suts'. Die Hauptneigung der SN-Kurve verläuft vom Zykluspunkt 1000 auf einen Lebensdauerwert, der der 'Ermüdungsgrenze' entspricht, und einer Spannungsamplitude entsprechend 'send'. Das Verhalten nach der Ermüdungsgrenze hängt davon ab, ob das Material ist eine Eisenlegierung oder keine Eisenlegierung ist. Es ist typisch für Stahl, eine echte Ermüdungsgrenze und eine Abflachung der SN-Kurve zu zeigen. Umgekehrt gilt, Aluminiumlegierungen und andere Nicht-Eisenlegierungen haben eine weniger ausgeprägte Abflachung der SN-Kurve bei hohen Zyklen. Der Assistent für die Ermüdungsberechnung ermöglicht dem Benutzer die Unterscheidung zwischen diesen beiden Fällen.
Mittlere Spannungseffekte
In der Regel werden SN-Kurven für einen vollständig umgekehrten Test angezeigt. Dies bedeutet, dass die angewendeten Spannungen zwischen gleichen Zug- und Druckspannungen wechseln. In realistischen Strukturbelastungen oszilliert die zyklische Belastung häufig um einen Mittelstatus ungleich Null. Dieser Mittelstatus ungleich Null hat erhebliche Auswirkungen auf die Lebensdauer bis zum Ausfall. Eine Methode ist erforderlich, um das Vorhandensein einer mittleren Spannung im Zyklus anzugeben, wenn standardmäßige SN-Daten verwendet werden.
Der Assistent für die Ermüdungsberechnung ermöglicht das Berechnen der Ermüdungslebensdauer ohne Korrektur oder nach Gerber- oder Goodman-Korrektur.
Spannungskonzentration
Normalerweise werden für FE-Analysen Modell Spannungen in Bereichen der lokalen Konzentration explizit modelliert und berechnet, sodass die Skalierung von Nennspannung wahrscheinlich nicht erforderlich ist. Sollte jedoch eine lineare Skalierung der berechneten FE-Spannungen erforderlich sein, bietet der Ermüdungsassistent einen allgemeinen Skalierungsfaktor Kt.
se = Kt.snominal
Dabei gilt: se = skalierte elastische Spannung
Ermüdungsgrenzen-Modifikatoren
Die SN-Kurvendaten werden normalerweise von Tests mit polierten Materialmustern in Standardgrößen angezeigt. Das Anwenden dieser 'Labor'-Testdaten in realen Konstruktionskomponenten erfordert manchmal einige Korrekturen. Die Korrekturen werden in der Regel als "Modifikatoren" auf die Materialermüdungsgrenze angewendet.
Modifikatoren können angewendet werden, um die Größe, Oberflächenbeschaffenheit, Spannungsverläufe, Oberflächenbehandlungen, Belastungstypen und so weiter zu berücksichtigen. Diese Modifikatoren sind in vielen Konstruktionstexten gut dokumentiert und stehen dem Ingenieur zur Verfügung, falls erforderlich.
send-modifiziert = send . nGröße . nOberfläche …
n ist der entsprechende Modifikator
Der Ermüdungsassistent liefert Standardmodifikatoren für Oberflächenbeschaffenheitseffekte und statistische Effekte und einen allgemeinen Modifikator zur Eingabe eines berechneten kombinierten Werts. Der Ermüdungsassistent ändert die SN-Kurve durch Skalierung der Materialermüdungsgrenze wie oben, und dreht die SN-Kurve über den Drehpunkt 1000.
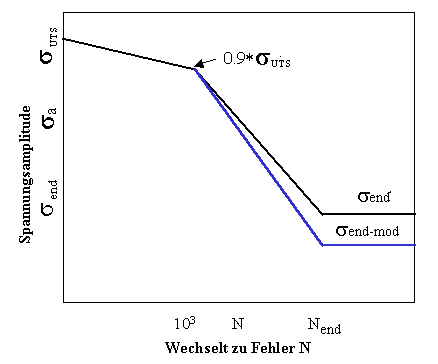
Abbildung 4
Dehnungs-Lebensdauer-Technik
Die Dehnungs-Lebensdauer-Technik wurde um 1960 als eine Verbesserung der Spannungs-Lebensdauer-Technik für die Ermüdungsbruchprognose in Materialien, die einer plastischen Verformung unterzogen werden, entwickelt. Das Prinzip ist insofern gleich, dass die Dehnungsamplitude (anstatt der Spannung) für eine zyklische Last gemessen oder berechnet wird und mit einem empirischen Diagramm der Dehnungsamplitude der Lebensdauer verglichen wird. Der Vorteil ist, dass es keine inhärente Annahme über die Testdaten zur vollständigen elastische Verformung gibt.
Dehnungs-Lebensdauer-Kurven
Dehnungs-Lebensdauer-Kurven beschreiben das Ermüdungsverhalten von im Labor getesteten Materialmustern. Materialmuster werden in der Regel unter vollständig umgekehrt Dehnung mit kontrollierter Belastung getestet und ins Verhältnis zur Lebensdauer-bis-zum-Bruch gesetzt. Eine empirische Kurve der Dehnungsamplitude mit Zyklen bis zum Ausfall wird geplottet.
Bei niedriger Belastung, bei der die Verformung vollkommen elastisch ist, bezieht sich das Ermüdungsverhalten auf die Spannungsamplitude und
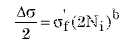
Dabei gilt: sf ist der Ermüdungsfestigkeitskoeffizient und b ist der Ermüdungsfestigkeitsexponent, beide aus der doppelt-logarithmischen Anpassung der Spannungsamplitude an die Lebensdauer.
Bei hoher Belastung, bei der die Verformung vorwiegend plastisch ist, bezieht sich das Ermüdungsverhalten am ehesten auf die Dehnungsamplitude, wie folgt
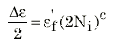
Dabei gilt: ef ist der Ermüdungsverformbarkeitskoeffizient und b ist der Ermüdungsverformbarkeitsexponent, beide aus der doppelt-logarithmischen Anpassung der plastischen Dehnungsamplitude an die Lebensdauer.
Die allgemeine Dehnungs-Lebensdauer-Kurve oder Coffin-Manson-Kurve wird als Kombination dieser beiden einzelnen geraden Linienkurven beschrieben, wie folgt
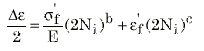
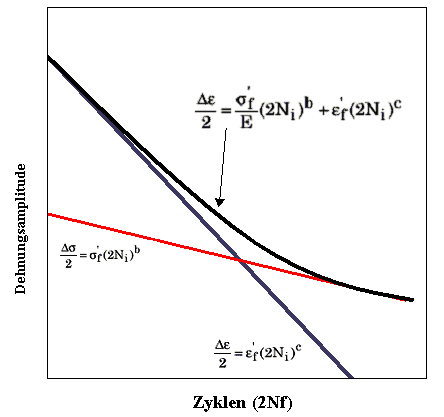
Abbildung 5 Dehnungs-Lebensdauer-Kurve mit konstanter Amplitude. Coffin-Manson-Beziehung.
Ungefähre verschiedene Dehnungs-Lebensdauer-Koeffizienten, die nicht verfügbar sind
Es gibt verschiedene Methoden, um die dehnungsbasierten Materialdaten aus den verfügbaren monotonen Daten, wie z. B. Zugfestigkeit, Modul usw. ungefähr zu schätzen. Die durch den Ermüdungsassistenten verwendete Methode ist die Methode nach Seeger/Beste. Sie steht in zahlreichen Texte zu dehnungsbasierten Ermüdungsberechnung zur Verfügung. Diese Technik schätzt die Dehnungs-Lebensdauer-Kurve (belastungsbasierte Koeffizienten) mit den folgenden Formeln:
Stahl:
- K' = 1.65 * UTS
- n' = 0.15
- Sf = 1.5 * UTS
- b= -0.087
- c= -0.58
- Ef = 0.59 (if UTS/E<0.003)
- Ef = 0.59*(1.375-125*UTS/E)
Andere:
- K' = 1.61 * UTS
- n' = 0.11
- Sf = 1.67 * UTS
- b= -0.095
- c= -0.69
- Ef = 0.535
Mittlere Spannungskorrektur
Die zuvor beschriebene Lebensdauer-Kurve mit konstanter Amplitude wird durch die Materialprüfung unter vollständig umgekehrter Belastung erzeugt, d. h. mit Mittelwertverschiebung Null. In wirklichkeitsgetreuen technischen Belastungszyklen, existiert L zwangsläufig mit einer mittleren Dehnung ungleich Null.
Um das Vorhandensein von Mittelwerten ungleich Null im Dehnungszyklus verwendet der Assistent für die Ermüdungsberechnung vzwei Korrekturen an der einfachen Dehnungs-Lebensdauer-Kurve, nämlich die Morrow-Korrektur und die Smith-Watson-Topper-Korrektur.
Dehnungs-Lebensdauer-Kurve mit Morrow-Korrektur
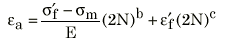
Dehnungs-Lebensdauer-Kurve mit SWT-Korrektur
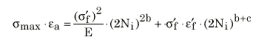
Elastisch-plastische Materialdaten
Da Dehnungs-Lebensdauer-Daten von Materialien extrahiert werden, die zyklischen Belastungen über die elastische Grenze hinaus ausgesetzt sind, ist es erforderlich, eine zyklische Spannungs-Dehnungs-Materialkurve zu definieren.
Der Ermüdungsassistent verwendet zwei ausführlich dokumentierte empirische Formeln für die Definition von zyklisch stabilen Spannungs-Dehnungs-Kurven.
Die zyklische Spannungs-Dehnungs-Kurve wird konstruiert, indem Sie die Ramberg-Osgood-Relation verwenden, um die Materialkonstanten K' und n' zu bestimmen. Das ist der zyklische Härtungskoeffizient und der zyklische Härtungsexponent.
Ramberg-Osgood-Relation
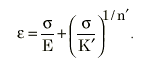
Um eine vollständige zyklische Spannungs-Dehnungs-Kurve zu erstellen, wird eine Masing-Theorie verwendet, wie folgt:
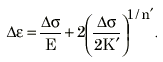
Durch die Kombination dieser beiden Beziehungen kann eine vollständige Hystereseschleife der zyklisch stabilen Spannungs-Dehnungs-Kurve aus den beiden Materialkonstanten erstellt werden.
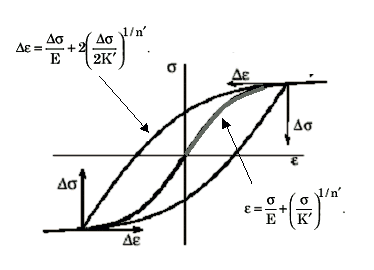
Abbildung 6 Zyklisch stabile Spannungs-Dehnungs-Kurve
Neuber-Korrektur
Viele FE-basierte Ermüdungscodes verwenden die Ergebnisse der elastischen FE-Analysen. Auf diese Weise können Sie relativ einfache FE-Berechnungen ausführen, ohne die Kosten und Zeit für die Ausführung nicht-linearer Lösungen. Wenn Sie später eine dehnungsbasierte Berechnung der Lebensdauer mit diesen elastischen Spannungen durchführen, verwenden Sie eine Methode für die Umwandlung der FE-basierten elastischen Spannung in eine entsprechende elastisch-plastische Spannung (und Dehnung).
Von den vielen vorgeschlagenen Methoden für diese Konvertierung, verwendet der Ermüdungsassistent die gängigste: die Neuber-Korrektur.
Spannungs-Lebensdauer-Ansatz
- Lesen Sie elastische Spannungsdaten aus den FE-Ergebnissen.
- Extrahieren Sie schlechteste absolute Hauptspannung.
- Skalieren Sie elastische Spannungen durch Kt.
- Extrahieren Sie Zyklen aus dem Zeitverlauf der Belastung mit Rainflow-Zählungen.
- Ändern Sie die SN-Kurve anhand der Ermüdungsgrenzen-Modifikatoren.
- Berechnen Sie den Schaden für Zyklen mit mittlerer Spannungskorrektur.
- Summieren Sie den Schaden entsprechend der linearn Miner-Regel.
- Geben Sie die Gebrauchsermüdung oder den Sicherheitskoeffizient für alle Knoten aus.
Dehnungs-Lebensdauer-Ansatz
- Lesen Sie elastische Spannungsdaten aus den FE-Ergebnissen.
- Extrahieren Sie schlechteste absolute Hauptspannung.
- Skalieren Sie elastische Spannungen durch Kt.
- Führen Sie eine Neuber-Korrektur zur lokalen Spannung aus.
- Konstruieren Sie vollständige lokale Spannungs/Dehnungs-Zeitverläufe mit zyklisch stabilen Spannungs/Dehnungs-Kurven.
- Extrahieren Sie alle geschlossenen Hystereseschleife im Zeitverlauf.
- Erstellen Sie eine Dehnungs-Lebensdauer-Kurve für einen einzelnen Zyklus aus den Materialdaten.
- Ändern Sie die Dehnungs-Lebensdauer-Kurven gemäß den Ermüdungsgrenzen-Modifikatoren.
- Berechnen Sie den Schaden für Zyklen mit mittlerer Spannungskorrektur.
- Summieren Sie den Schaden entsprechend der linearn Miner-Regel.
- Geben Sie die Gebrauchsermüdung oder den Sicherheitskoeffizient für alle Knoten aus.