Auf die eine oder andere Weise dient die Finite-Elemente-Methode (FEM) zum Lösen von Gleichungen. In dem einfachen Modell mit zwei Federn, das weiter unten dargestellt ist, sind F1 und F2 die angewendeten Lasten, K1 und K2 die Steifheit der Federn und X1 und X2 die Verformungen an jedem Ende. Beachten Sie, dass jede der angewendeten Lasten Null sein kann (beide Lasten sind jedoch bekannte Werte). Die in jeder Feder entwickelte Kraft durch Verlängerung ist unbekannt, aber sie kann mithilfe der direkten Formel F = k * x berechnet werden. Wenn Feder 1 um den Betrag X1 und Feder 2 um den Betrag (X2 - X1) verlängert wird, lautet die Gleichung für die Summe der Kräfte an jedem Knoten folgendermaßen:
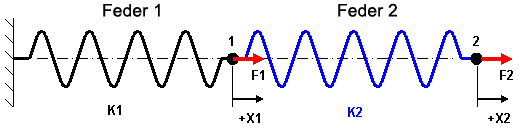
| F1 - K1 * X1 + K2 * (X2 - X1) = 0 | Knoten 1 |
| F2 - K2 * (X2 - X1) = 0 | Knoten 2 |
Eine Neuanordnung der Gleichungen ergibt:
| F1 = (K1 + K2) * X1 - K2 * X2 | Knoten 1 |
| F2 = -K2 * X1 + K2 * X2 | Knoten 2 |
Diese Gleichungen können in Matrizenschreibweise folgendermaßen ausgedrückt werden:
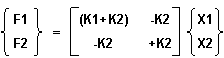
Kurzschreibweise: {F} = [K]{X}.
Wie die Gleichungsmatrix in FEM gelöst wird, ist die Aufgabe des Solvers. Entsprechend der Weiterentwicklung der Computerhardware und Berechnungstechniken werden neue Solver zur Software hinzugefügt. Für jeden Analysetyp stehen verschiedene Solver zur Auswahl. In vielen Fällen ist die Standardoption Automatisch. Bei dieser Einstellung wählt die Software den Solver aus, der am besten für die Analyse geeignet ist (dies richtet sich gewöhnlich nach der Größe des Modells (die Anzahl der Gleichungen). Die folgenden Informationen beschreiben die allgemeine Methodik für jeden Solvertyp.
Je nachdem, wie die Elemente miteinander verbunden sind, ist die Steifheitsmatrix [K] in der Regel sehr dünnbesetzt. Viele der Einträge sind Null. Da der Wert Null keinen Beitrag zur Lösung leistet, sind die meisten Lösungstechniken auf die eine oder andere Weise so programmiert, dass die Null-Elemente ignoriert werden. Eine Methode benötigt eine geringe Menge an Arbeitsspeicher zum Speichern der Matrix, muss aber optimiert werden, um so wenig Speicherplatz wie möglich zu belegen. Eine andere Methode verwendet mehrere Variablen zum Speichern der Matrix (und benötigt daher mehr Arbeitsspeicher), sie kann jedoch schneller ausgeführt werden.
Als Nächstes ermittelt die Lösung für den Gleichungssatz, wie lange die Ausführung der Analyse dauert. Es gibt direkte Lösungsmethoden, die gewährleisten, dass eine Lösung gefunden wird, wenn das Modell ordnungsgemäß eingerichtet wurde (das Modell für die statische Spannung ist ordnungsgemäß verbunden, das Modell für die stationäre Wärmeübertragung verfügt über eine Wärmequelle und eine Möglichkeit zur Entfernung der Wärme usw.). Techniken wie das Gaußsche Eliminationsverfahren und die Matrixinversion sind einfache Beispiele für direkte Lösungsmethoden. Außerdem gibt es indirekte Lösungsmethoden, in denen eine Lösung angenommen wird. Durch Einsetzen der angenommenen Lösung in das Gleichungssystem kann jeder unbekannte Wert besser geschätzt werden. Dieser Vorgang wird so lange wiederholt, bis sich die Lösung nicht mehr ändert. Aus diesem Grund sind diese Techniken als iterative Lösungsmethoden bekannt.
Letztendlich ist die Steifheitsmatrix in FEM im Allgemeinen symmetrisch. In diesen Fällen müssen nur die Elemente auf und über der Diagonalen gespeichert werden. Dies reduziert den Speicherplatzbedarf und die Anzahl der Operationen zum Lösen der Matrix. Wenn ein Effekt enthalten ist, der dazu führt, dass die Matrix unsymmetrisch ist (z. B. Strahlung zwischen Körpern in einer Wärmeübertragungsanalyse oder ein Auslöser in einem mechanischen Ereignissimulator), muss die gesamte Matrix gespeichert und bearbeitet werden. In solchen Fällen ist die Lösung länger.
Nachfolgend sind die allgemeinen Solver aufgeführt, die verfügbar sind. Jeder Solver kann Variationen für einen bestimmten Analysetyp aufweisen. Beispielsweise verfügt die Modalanalyse über einen iterativen Solver (Unterraum), der eine Variation des iterativen Solvers ist, der für lineare statische Spannungsanalysen (AMG, Algebraisches Mehrgitter) verfügbar ist. Der Typ des Solvers, der in der Analyse verwendet wird, wird über Setup 
Modell einrichten Parameter eingerichtet (oder klicken Sie mit der rechten Maustaste in der Strukturansicht auf den Eintrag Analyseart, und wählen Sie Analyseparameter bearbeiten).
Sparse Solver
- Bietet eine direkte Lösung der Matrix.
- Die Bandbreite wird nicht optimiert, sodass der Zeitaufwand für die Optimierung entfällt.
- Statt die gesamte Matrix zu speichern, werden nur die Elemente ungleich Null gespeichert. (Davon leitet sich der Name Sparse Solver ab, da sparse "dünnbesetzt" bedeutet.)
- Es werden zwar weniger Elemente aus der Steifheitsmatrix gespeichert, aber es sind mehr Variablen erforderlich, um die Position der Elemente ungleich Null zu speichern. Aus diesem Grund benötigt der Sparse Solver mehr Arbeitsspeicher als die anderen Solver.
- Der Sparse Solver ist die schnellste Lösung für mittelgroße Modelle.
Iterativer Solver
- Bietet eine indirekte Lösung der Matrix. Daher muss der Benutzer angeben, wie oft die Iterationen maximal durchgeführt werden und anhand welcher Konvergenzkriterien bestimmt wird, ob die Lösung konvergiert. Es kann nicht garantiert werden, dass die Lösung der Matrix im Rahmen der angegebenen Anzahl von Iterationen gefunden wird.
- Da der iterative Solver mit einer Schätzung beginnt, verfügen einige der Gleichungslöser über einen Vorbehandler. Dadurch stehen mehr Optionen zur Auswahl, mit denen das Modell effizient gelöst werden kann.
- Die Bandbreite wird nicht optimiert, sodass der Zeitaufwand für die Optimierung entfällt.
- Der iterative Solver benötigt weniger Speicherplatz als der Sparse Solver.
- Wenn Konvergenz möglich ist, ist der iterative Solver die schnellste Lösung für große Modelle. Es ist von der Art der Analyse abhängig, wann ein Modell als groß bezeichnet wird. In linearen statischen Spannungsanalysen sind 150.000 Gleichungen (oder Freiheitsgrade) groß. In Strömungsanalysen können 50.000 Gleichungen groß sein. Achtung: Die Genauigkeit der Lösung hängt von der Konvergenztoleranz ab. Kleinere Toleranzwerte ergeben eine genauere Lösung, benötigen jedoch u. U. mehr Iterationen. Wie bei allen iterativen Lösungen sollten die Ergebnisse geprüft werden, um zu bestätigen, dass sie die entsprechende Genauigkeit aufweisen. In einigen Fällen ist die beste Methode zum Bestätigen der Genauigkeit, die Analyse zweimal mit unterschiedlichen Konvergenztoleranzen auszuführen.Anmerkung: Der iterative Prozess zum Lösen der Matrix ist eine erforderliche Konvergenzebene. Dieser Prozess stellt die Lösung für die Gleichungen bereit. Wenn die Analyse auch nichtlinear ist, muss das Problem wiederholt gelöst werden, um zur physischen Lösung zu konvergieren. Beispielsweise führt Strahlung dazu, dass die zu lösenden Gleichungen nichtlinear sind. Infolgedessen sind mehrere Iterationen erforderlich, um die Lösung für die nichtlinearen Gleichungen zu finden. (Normalerweise sind die Gleichungen linear und erfordern nur eine Lösung.) Der iterative Prozess zum Lösen des Modells darf nicht mit dem iterativen Prozess zum Lösen des Gleichungssystems verwechselt werden.Tipp: Wenn die Analyse nicht mit dem iterativen Solver konvergiert und die Meldung ausgibt, dass die Matrix möglicherweise nicht positiv definit ist bzw. welche Bedingung für das vorausgesetzte System vorliegt, wird das Problem u. U. durch ein statisch instabiles Modell verursacht. Stellen Sie in einer statischen Spannungsanalyse sicher, dass alle Komponenten statisch stabil sind. Wenn das Modell Kontaktflächen umfasst, finden Sie Vorschläge auf der Seite Einrichten und Durchführen der Analyse: Durchführen der Analyse: Durchführen einer linearen Analyse: Durchführen von Analysen mit Lückenelementen.