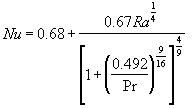Externer Fluss
Das Listenfeld Externer Fluss enthält zwei Optionen. Beide sind auf laminare Strömungen über eine flache Oberfläche ausgelegt, die auf konstanter Temperatur ([T]) gehalten wird. Der Unterschied zwischen den beiden Optionen besteht im Wertbereich der Reynolds- und Prandtl-Zahlen. Die Reynolds- und Prandtl-Zahlen werden wie folgt berechnet.
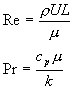
Dabei gilt:
ρ = Dichte der Flüssigkeit
U = Charakteristische Fließgeschwindigkeit
L = Längenskala (Eingabe durch den Benutzer auf der Registerkarte Geometrie)
μ = dynamische Viskosität der Flüssigkeit
c p = Spezifische Wärme der Flüssigkeit
k = thermische Leitfähigkeit der Flüssigkeit
Nachfolgend werden die Gleichungen beschrieben, die zur Ermittlung der Nusselt-Zahl für jede Option verwendet werden.
[T] laminarer Fluss entlang einer flachen Platte (0,6<Pr<50):
- Nu=0.664Re 1/2 Pr 1/3 Alle Eigenschaften werden bei Filmtemperatur Tf evaluiert.
[T] Laminarer Fluss entlang einer flachen Platte (Pr>>1, Re<500.000:
- Nu=0.678Re 1/2 Pr 1/3 Alle Eigenschaften werden bei Filmtemperatur Tf evaluiert.
Interner Fluss
Das Listenfeld Interner Fluss enthält 12 Optionen für 3 Gehäusegeometrien. Diese Optionen umfassen turbulente und laminare Strömungen sowie Oberflächen mit konstanter Temperatur [T] oder mit Erwärmung durch einen konstanten Wärmefluss [Q]. Bei einigen dieser Optionen wird die Nusselt-Zahl aus den Reynolds- und Prandtl-Zahlen ermittelt, einige Optionen sind jedoch von diesen Zahlen unabhängig. Die Reynolds- und Prandtl-Zahlen werden wie folgt berechnet.
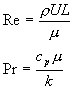
Dabei gilt:
ρ = Dichte der Flüssigkeit
U = Charakteristische Fließgeschwindigkeit
L = Längenskala (Eingabe durch den Benutzer auf der Registerkarte Geometrie)
μ = dynamische Viskosität der Flüssigkeit
c p = Spezifische Wärme der Flüssigkeit
k = thermische Leitfähigkeit der Flüssigkeit
Die folgenden Begriffe aus den Optionsbeschreibungen werden wie folgt definiert:
- L/D: Dies ist das Verhältnis zwischen Eingangslänge und Durchmesser des Rundrohrs oder das Verhältnis der Eingangslänge zum hydraulischen Radius einer rechteckigen oder dreieckigen Leitung.
- Hydro: Dies verweist auf den hydraulischen Radius. Dies kann mit 4A/P berechnet werden, wobei A der Querschnittsbereich und P der Querschnittumfang ist.
- Kaltwand: Dies verweist auf eine Situation, bei der die Wand kälter ist, als die Flüssigkeit. Daher erwärmt die Flüssigkeit die Wand.
- Heißwand: Dies verweist auf eine Situation, bei der die Wand wärmer ist, als die Flüssigkeit. Daher kühlt die Flüssigkeit die Wand.
Nachfolgend werden die Gleichungen beschrieben, die zur Ermittlung der Nusselt-Zahl für jede Option verwendet werden. Alle Eigenschaften für diese internen Strömungsgleichungen werden bei Massenmaterialtemperatur Tb evaluiert.
[Q] Laminar, Rundrohr (Pr>0.6):
- Nu=4.36
[T] Laminar, Rundrohr (Pr>0.6):
- Nu=3.66
[T] Turbulent, Rundrohr (Re>10k, L/D>10, Heißwand):
- Nu=0.023Re 4/5 Pr 0.4
[T] Turbulent, Rundrohr (Re>10k, L/D>10, Kaltwand):
- Nu=0.023Re 4/5 Pr 0.3
[Q] Laminar, rechteckige Leitung (Pr>0.6, Hydro):
- Nu=4.36
[T] Laminar, rechteckige Leitung (Pr>0.6, Hydro):
- Nu=3.66
[T] Turbulent, rechteckige Leitung (Re>10k, L/D>10, Heißwand):
- Nu=0.023Re 4/5 Pr 0.4
[T] Turbulent, rechteckiger Leitung (Re>10k, L/D>10, Kaltwand):
- Nu=0.023Re 4/5 Pr 0.3
[Q] Laminar, dreieckige Leitung (Pr>0.6, Hydro):
- Nu=4.36
[T] Laminar, dreieckige Leitung (Pr>0.6, Hydro):
- Nu=3.66
[T] Turbulent, dreieckige Leitung (Re>10k, L/D>10, Heißwand):
- Nu=0.023Re 4/5 Pr 0.4
[T] Turbulent, dreieckige Leitung (Re>10k, L/D>10, Kaltwand):
- Nu=0.023Re 4/5 Pr 0.3
Auftriebsströmung
Das Listenfeld Auftriebsströmung umfasst acht Optionen für drei Gehäusegeometrien. Diese Optionen umfassen turbulente und laminare Strömungen sowie Oberflächen mit konstanter Temperatur [T] oder mit Erwärmung durch einen konstanten Wärmefluss [Q]. Die Nusselt-Zahl wird mithilfe der Grashof-, Prandtl- und Rayleigh-Zahlen berechnet. Die Grashof-, Prandtl- und Rayleigh-Zahlen werden mit den folgenden Gleichungen berechnet.
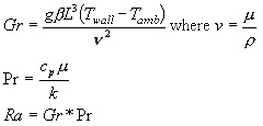
Dabei gilt:
g = Beschleunigung aufgrund der Schwerkraft
β = Wärmeausdehnungskoeffizient (für ideales Gas, β = 1/T, wobei T die absolute Gastemperatur ist.)
L = Längenskala (Durchschnitt von Höhen- und Breiteneingabe des Benutzers auf der Geometrie-Registerkarte)
T Wand = Wandtemperatur
T Umg = Umgebungstemperatur der Flüssigkeit
ν = kinematische Viskosität der Flüssigkeit
μ = dynamische Viskosität des Fluids
ρ = Dichte des Fluids
c p = spezifische Wärme des Fluids
k = thermische Leitfähigkeit der Flüssigkeit
Nachfolgend werden die Gleichungen beschrieben, die zur Ermittlung der Nusselt-Zahl für jede Option verwendet werden. Alle Eigenschaften für diese Auftriebsgleichungen werden bei Filmtemperatur Tf evaluiert.
[T] Laminar, vertikale Platte:
[T] Turbulent, vertikale Platte:
[T] Laminar, horizontale Platte (nach oben weisend, 100k<Ra<10M): (obere Fläche einer heißen Platte oder untere Fläche einer kalten Platte)
- Nu=0.54Ra 1/4
[T] Turbulent, horizontale Platte (nach oben weisend, 20M<Ra<30G): obere Fläche einer heißen Platte, oder untere Fläche einer kalten Platte)
- Nu=0.14Ra 1/3
[T] Laminar, horizontale Platte (nach unten weisend, 300k<Ra<30G): (untere Fläche einer heißen Platte oder obere Fläche einer kalten Platte)
- Nu=0.27Ra 1/4
[Q] Laminar, horizontale Platte (nach oben weisend, Ra<200M): (obere Fläche einer heißen Platte oder untere Fläche einer kalten Platte)
- Nu=0.13Ra 1/3
[Q] Laminar, horizontale Platte (nach oben weisend, 500M<Ra<100G): (obere Fläche einer heißen Platte oder untere Fläche einer kalten Platte)
- Nu=0.16Ra 1/3
[Q] Laminar, horizontale Platte (nach unten weisend, 1M<Ra<100G): (untere Fläche einer heißen Platte oder obere Fläche einer kalten Platte)
- Nu=0.58Ra 1/5