Bodenbewegung - Vibration unterstützen

Ausgangssituation: Ein flexibles System mit einer sich bewegenden Basis besteht aus einem Körper mit einer Masse von 225 kg, einer Steifigkeit des Tragwerks von 35000 N/m und einem Dämpfungsfaktor von 0.188. Die Basis oszilliert sinusförmig mit einer Amplitude von 0.280 cm in der Eigenfrequenz des Systems.

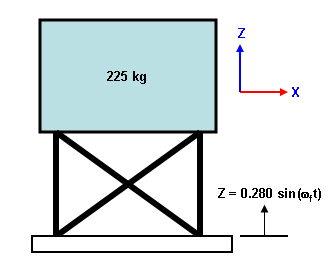Die physische Baugruppe.

Die Basis wird mit der Eigenfrequenz des Tragwerks vibriert.

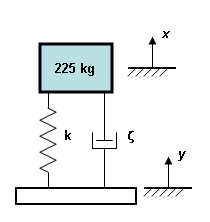Die entsprechende Darstellung.

k = 35000 N/m

ζ = 0.188

x und y werden in Fachbüchern über Vibration als typische Nomenklatur zur Messung der absoluten Bewegung von Masse und Basis verwendet. Die Nomenklatur von x und y in Kleinbuchstaben und kursiv gibt die Position als Funktion der Zeit an.

Suchen:

Die Amplitude der Verschiebung der Masse relativ zur Basis.
Die absolute Amplitude der Verschiebung der Masse (Verschiebung relativ zu einer nicht beweglichen Quelle).

Anstatt das gesamte Tragwerk im Detail zu modellieren, kann es auch mit Stabelementen dargestellt werden. (Erinnern Sie sich, die Steifigkeit eines Stabelements k ist A*E/L.) Die Masse kann durch eine konzentrierte Masse dargestellt werden, die am Ende des Stabs hinzugefügt wird. Die sich bewegende Basis wird durch eine feste Begrenzungsbedingung dargestellt und eine Bodenbewegung oder Basis-Beschleunigungslast wird die Schwingung der Basis simulieren. Das Ende des Stabelements mit der Masse hat eine Begrenzungsbedingung, die die Schwingung der Masse auf die Axialrichtung beschränkt.

Schritte

Führen Sie eine Eigenfrequenzanalyse (Modalanalyse) durch, um die Eigenfrequenz zu erhalten. Neben der Angabe der Frequenz (wird in der Problembeschreibung benötigt) werden die Ergebnisse der Modalanalyse von den nächsten beiden Analysearten verwendet.
Führen Sie eine Frequenzantwortanalyse mit Grundbeschleunigung durch, um die fast stationäre Zustandsamplitude der Masse zu erhalten. Frequenzantwort simuliert eine auf das Modell angewendete Sinuslast.
Um zu prüfen, was mit dem System passiert, das bei 0 Geschwindigkeit startet, führen Sie eine transiente Spannungsanalyse (Modale Überlagerung) mit Grundbeschleunigung durch. Die transiente Spannung berechnet die Antwort des Modells auf eine allgemeine Last anhand einer benutzerdefinierten Lastkurve. Tritt während der zeitabhängigen Spannung eine höhere Abweichung auf?

Erstellen des Modells:

Starten Sie ein neues FEM-Modell.
1. Legen Sie als Analyseart Linear: Eigenfrequenz (Modalanalyse) fest.
2. Da die Schwingung in Zentimetern angegeben ist, können Sie die Einheiten Newton, Zentimeter und Sekunden für das Modell auswählen. Klicken Sie auf Standardeinheiten überschreiben, und wählen Sie im Dropdown-Feld Einheitensystem die Option Benutzerdefiniert. Legen Sie dann die entsprechenden Einheiten für Kraft, Länge und Zeit jeweils auf N, cmund s fest. Klicken Sie auf OK, um die Einheiten festzulegen.
3. Klicken Sie auf Neu, und geben Sie einen Modellnamen ein.
Fügen Sie mit Zeichnen Zeichnen Linie eine Linie ein, die für die Tragwerkkonstruktion steht. Das Kontrollkästchen Als Konstruktion verwenden, muss deaktiviert sein. Die Ausrichtung kann in eine beliebige Richtung erfolgen, da Stabelemente dreidimensional sind. Aus Gründen der Konsistenz verwenden wir jedoch die Ausrichtung aus dem vorherigen Bild. Das Element kann beliebig lang sein (sofern die Kombination A*E/L zur korrekten Steifigkeit führt). Wählen Sie daher eine Länge von 2 cm. Beginnen Sie die Linie bei (0,0,0), und setzen Sie den nächsten Endpunkt bei (0,0,2). Schließen Sie das Dialogfeld.
Schließen Sie das gesamte Modell ein (Ansicht Navigieren Einschließen).
Legen Sie als Elementtyp Stab fest. Klicken Sie in der Strukturansicht mit der rechten Maustaste auf die Überschrift Elementtyp, und wählen Sie Stab.
Legen Sie die Eigenschaften des Stabs mithilfe der Elementdefinition fest. Klicken Sie mit der rechten Maustaste auf die Überschrift Elementdefinition, und wählen Sie Elementdefinition bearbeiten. Sie können die Querschnittfläche auf einen beliebigen Wert einstellen. Geben Sie daher einen Wert von 1 cm² ein, und klicken Sie auf OK.
Um die Eingabe zu erleichtern, insbesondere für die Ausdrücke im Zusammenhang mit Masse, definieren Sie eine Anzeigeeinheit mit kg als Masseeinheit.
1. Klicken Sie mit der rechten Maustaste im oberen Bereich der Strukturansicht auf die Verzweigung Einheitensystemen, und wählen Sie Neu.
2. Stellen Sie im Dropdown-Menü System die Option Benutzerdefiniert ein, und stellen Sie die entsprechenden Einheiten für Kraft, Länge, Zeit und Masse auf N, cm, s und kg ein.
3. Geben Sie eine Beschreibung ein, z. B. N cm kg.
4. Klicken Sie auf OK, um die Anzeigeeinheiten festzulegen und zu aktivieren.
Geben Sie die Materialeigenschaften ein. Klicken Sie in der Strukturansicht mit der rechten Maustaste auf die Überschrift Material, und wählen Sie den Befehl Material bearbeiten aus. Da die Länge und die Querschnittsfläche für das Element festgelegt wurden, können die Materialeigenschaften nicht beliebig ausgewählt werden. Das Elastizitätsmodul muss 700 N/cm² sein, damit die entsprechende Steifigkeit erzielt wird. [k = 35000 N/m = 350 N/cm = A*E/L = (1 cm²)*(700 N/cm²)/(2 cm)]. Wählen Sie den Eintrag [Anwenderdefiniert], und klicken Sie auf Eigenschaften bearbeiten. Geben Sie ein Elastizitätsmodul von 700 N/cm² ein. Um mögliche Lösungsprobleme durch eine Nullmasse in den Elementen zu vermeiden, geben Sie eine Massendichte von 0,05 kg/cm³ ein. Basierend auf der zuvor ausgewählten Länge und Fläche hat das Element nun eine Gesamtmasse von 1 kg. Dies ist im Vergleich zur angewendeten Masse von 225 kg unbedeutend. Klicken Sie zweimal auf OK, um die Eigenschaften festzulegen.
Fügen Sie dem Modell die Begrenzungsbedingungen hinzu. Wählen Sie den Knoten am unteren Ende der Feder (Auswahl Form Punkt oder Rechteck und Auswahl Auswählen Knoten), klicken Sie mit der rechten Maustaste, und wählen Sie Hinzufügen Knotenrandbedingung. Klicken Sie auf Keine Übersetzung, um den Knoten in X-, Y- und Z-Translation (Tx, Ty, Tz) zu fixieren. Klicken Sie auf OK, um die Begrenzungsbedingung anzuwenden. (Eine Begrenzungsbedingung Fixiert wäre in dieser Situation ebenfalls möglich, da das Stabelement über keine Rotations-Freiheitsgrade verfügt).
Wählen Sie den Knoten am oberen Ende der Feder (Auswahl Form Punkt oder Rechteck und Auswahl Auswählen Knoten), klicken Sie mit der rechten Maustaste, und wählen Sie Hinzufügen Knotenrandbedingung. Die Feder muss in die Axialrichtung (Z) frei verschiebbar sein, darf jedoch nicht umkippen. Aktivieren Sie die Kontrollkästchen für Tx und Ty. Klicken Sie auf OK, um die Begrenzungsbedingung anwenden.
Fügen Sie die Masse der Struktur bei ausgewähltem oberen Knoten hinzu. Klicken Sie mit der rechten Maustaste, und wählen Sie Hinzufügen Knotenmassenkonzentration. Stellen Sie sicher, dass die Option für Masseneinheit aktiviert ist, und geben Sie den Wert 225 für die X-Richtung der Masse in Kilogramm ein. (Das Kontrollkästchen Einheitlich sollte aktiviert sein, sodass die Masse in alle drei Richtungen gleichmäßig agiert.) Klicken Sie auf OK, um die konzentrierte Masse anwenden.
Wie in der Zeichnung ersichtlich, hat das Modell nur einen Knoten, der nur in eine Richtung (Z-Translation) verschoben werden kann. Dies ermöglicht einen Freiheitsgrad. Aus Gründen, auf die hier nicht weiter eingegangen werden kann, ist dieses Modell zu klein, um in FEM gelöst zu werden! Das Modell benötigt einige weitere Freiheitsgrade (oder Gleichungen). Wählen Sie also die Linie (Auswahl Form Punkt oder Rechteck und Auswahl Auswählen Linien), und unterteilen Sie sie in vier Abschnitte (Zeichnen Ändern Teilen 4 OK). Auf diese Weise werden drei neue Knoten erstellt, mit denen der Solver arbeiten kann. Diese neuen Knoten müssen nun eingeschränkt werden, sodass sie sich nur in Axialrichtung bewegen. Wählen Sie die Knoten aus, indem Sie einen Rahmen um sie ziehen (Auswahl Form Rechteck und Auswahl Auswählen Knoten). Klicken Sie mit der rechten Maustaste, und wählen Sie Hinzufügen Knotenrandbedingung. Beachten Sie, dass in der Titelleiste des Dialogfelds angezeigt wird, dass drei Objekte für Knotenrandbedingungen erstellt werden. Aktivieren Sie die Kontrollkästchen Tx und Ty. Klicken Sie auf OK, um die Begrenzungsbedingung anzuwenden.

Im letzten Schritt vor der Ausführung der Modalanalyse richten Sie die Parametern für die Anzahl der Modi und Frequenzen ein. Wählen Sie Setup Modell einrichten Parameter, und geben Sie 1 für Anzahl der zu berechnenden Frequenzen/Modi ein. Klicken Sie auf OK. (Da wir ein Modell mit einem Freiheitsgrad von 1 erstellt haben, muss nur eine Frequenz berechnet werden.)

Schritt 1: Durchführen der Eigenfrequenzanalyse

Führen Sie die Analyse mit dem Befehl Analyse Analyse Simulation ausführen aus. Wenn die Analyse abgeschlossen ist, wird das Modell in der Ergebnisanzeige angezeigt. Beachten Sie die Eigenfrequenz: 1.985 Zyklen/Sekunde.

Schritt 2: Durchführen der Frequenzantwortanalyse

Kehren Sie zur Registerkarte FEM-Editor zurück.
Um eine stationäre Durchbiegung aufgrund der oszillierenden Basis zu vermeiden, stellen Sie als Analyseart Frequenzantwort ein (Analyse Typ Linear Frequenzantwort). Wenn Sie aufgefordert werden, das Modell in ein neues Entwurfsszenario zu kopieren, klicken Sie auf Ja. Die Ergebnisse der Eigenfrequenz sind im Entwurfszenario 1, die Ergebnisse der Frequenzantwort in Entwurfszenario 2 enthalten und können jeweils durch Auswahl des Entwurfszenarios schnell aufgerufen werden.
Für diese Art der Analyse werden alle Eingaben über die Analyseparameter eingegeben. Wählen Sie Setup Modell einrichten Parameter, und klicken Sie dann auf Einstellungen der Analyse. (Die Optionen unter Ausgabesteuerelemente sind nur für zusätzliche textbasierte Ausgaben gedacht. Sie müssen in der Regel nicht aktiviert werden.) Die vollständige Definition der Lasten wird in vier Registerkarten eingegeben. Die Eingabe auf den Registerkarten kann wie folgt zusammengefasst werden:
1. Die Position der Lasten wird auf der Registerkarte Erregte Knoten angegeben. Die Frequenz und Amplitude der Last wird jedoch auf dieser Registerkarte nicht angegeben. Stattdessen wird die Position mit den zwingenden Frequenzen verknüpft, indem der Index der Erregerfrequenzdefinition angegeben wird. (In einigen Fällen ist es besser, die anderen Registerkarten zuerst und die Registerkarten Erregte Knoten erst zum Schluss auszufüllen).
2. Die Frequenz der Erregung ist auf der Registerkarte Erregerfrequenzen angegeben, die Amplitude der Last ist jedoch nicht auf dieser Registerkarte angegeben. Wenn Sie daher einen Sinus Sweep Test annähern, geben Sie auf dieser Registerkarte mehrere Zeilen mit unterschiedlicher erzwungener Frequenz ein, von der minimalen bis zur maximalen Frequenz in Schritten von f.
3. Die Dämpfung des Modells wird auf der Registerkarte Dämpfungsverhältnis eingegeben. Diese Tabelle ist an jeder Erregerfrequenz interpoliert, um den Dämpfungsgrad an den einzelnen zwingenden Frequenzen zu bestimmen. Die Frequenzen in dieser Tabelle müssen daher nicht die Tabelle der vorhandenen Erregerfrequenzen duplizieren, sondern den gesamten Bereich der Erregerfrequenzen abdecken.
4. Die Amplitude der angewendeten Lasten wird auf der Registerkarte Amplituden eingegeben. Diese Tabelle ist an jeder Erregerfrequenz interpoliert, um die Größe der sinusförmigen Last an den einzelnen zwingenden Frequenzen zu bestimmen. Die Frequenzen in dieser Tabelle müssen daher nicht die Tabelle der vorhandenen Erregerfrequenzen duplizieren, sondern den gesamten Bereich der Erregerfrequenzen abdecken.
Da die Frequenzantwortanalyse die Ergebnisse aus der Modalanalyse verwendet, geben Sie in das Feld Modale Ergebnisse aus Entwurfsszenario verwenden den Wert 1 ein.
Auf der Registerkarte Erregte Knoten wird definiert, wo sich die sinusförmigen Lasten befinden. Legen Sie für dieses Beispiel die folgenden Werte fest:
1. Wählen Sie die Option Grundbeschleunigungsbewegung im Abschnitt Knotennummer, um anzugeben, dass die Grundlager vibriert werden.
2. Da die Last eine Grundbeschleunigung ist, muss als Typ der Erregung Beschleunigungseingabe, nichtKrafteingabe angegeben werden.
3. Wählen Sie als Richtung, in der die Basis vibriert wird, die Option Z-Richtung im Abschnitt Richtung der Erregung. Alle Knoten im Modell, die in Z-Richtung eingeschränkt sind, werden als an der Basis angebracht angesehen und daher vibriert.
4. Geben Sie als Skalierungsfaktor für Amplituden 1 an. Dieser Wert skaliert die angewendeten Lasten.
Auf der Registerkarte Erregungsfrequenzen wird definiert, mit welcher Frequenz (oder Frequenzen) das Modell vibriert wird. In diesem Beispiel müssen wir nur eine Frequenz in die Tabelle eingeben: 1.985 Hz.
Auf der Registerkarte Dämpfungsverhältnisse wird der Dämpfungsgrad als Funktion der Frequenz definiert. Wenn nur eine Zeile in die Tabelle eingegeben wird, ist die Dämpfung für alle zwingenden Frequenzen konstant. Geben Sie also eine Frequenz von 1 Hz und ein Dämpfungsverhältnis von 0.188 ein (wie in der Problemangabe beschrieben.
Auf der Registerkarte Amplituden wird die Größe der angewendeten Last (entweder eine Beschleunigung oder eine Kraft) als Funktion der Frequenz definiert. Dieses Modell verwendet die Grundbeschleunigung, aber in der Problembeschreibung wird die Amplitude der Grundbewegung angegeben. Um die Beschleunigung zu erzielen, nehmen Sie einfach die zweite Ableitung der Verschiebung (y = 0.280*sin(ωt)), um die Gleichung der Beschleunigung (ay = -0.280*ω^2*sin(ωt)) zu erhalten. Die berechnete Beschleunigungsamplitude ist daher = (0.280 cm)*[(1.985 Zyklen/Sek)*(2*pi Bogenmaß/Zyklus)]^2 = 43.55 cm/sec^2. Die Benutzeroberfläche verwendet Beschleunigung in Einheiten von Gs, teilen Sie daher die Beschleunigungsamplitude durch die Schwerkraftkonstante, um (43.55 ^ 2) /(981 cm/s ^ 2) = 0.0444 G zu erhalten. Für eine konstante Last, die über alle angewendeten Frequenzen verteilt ist, geben Sie eine Zeile ein, wie z. B. Frequenz = 1 und Beschleunigung = 0.0444. (Da keine Kräfte auf das Modell angewendet werden, kann die Spalte Kraft leer bleiben.)
Klicken Sie zweimal auf OK, um die Analyseparameter anzuwenden.
Führen Sie die Analyse mit dem Befehl Analyse Analyse Simulation ausführen durch. Wenn die Analyse abgeschlossen ist, wird das Modell in der Ergebnisanzeige angezeigt.
Als Ergebnisse werden die relativen Verschiebungen ausgegeben. (Beachten Sie, dass die Verschiebung der Basis als 0, nicht als die eingegebene Amplitude von 0.280 cm angezeigt wird.) Da das Modell in alle Richtungen mit Ausnahme der Z-Richtung eingeschränkt ist, entspricht der als Größe der Verschiebung erhaltene Wert dem Wert der Z-Verschiebung. Zum Zweck der Präsentation, ist es jedoch möglicherweise besser, das Ergebnis der Z-Verschiebung anzuzeigen. Verwenden Sie den Befehl Ergebniskonturen Verschiebung Z.
Die Ergebnisse einer Frequenzantwortanalyse werden als In-Phase-Ergebnisse, phasenverschobene Ergebnisse und SRSS-Ergebnisse angegeben. Zeigen Sie die einzelnen Arten im Dropdown-Menü Ergebnisoptionen Analysespezifisch Antworttyp an. Da die In-Phase Komponente in diesem Beispiel nahezu null ist, sind die phasenverschobenen und SRSS-Ergebnisse identisch. Der Körper verschiebt sich um maximal 0.745 cm relativ zur Basis.

Die absolute Verschiebung der Masse lässt sich wie folgt berechnen. (Siehe die Nomenklatur in Abbildung 1. X, Y, Z sind die absoluten Positionen zum Zeitpunkt t. X, Y, Z sind die maximalen Werte oder Amplituden über den gesamten Zyklus.)

Relative Verschiebung z	=	x - y
Absolute Verschiebung x	=	z + y
Die Bewegung der Basis wird angegeben als y	=	Y * sin (ωt)
und die relative Verschiebung z	=	Z * sin (ωt-φ), wobei φ der Phasenwinkel ist.
Daher ist x	=	Z * sin(ωt-φ) + Y*sin(ωt)

In der Übersichtsdatei zur Frequenzantwort (Zugriff über die Berichtsumgebung) liegt der berechnete Phasewinkel im Wesentlichen bei 90 Grad (siehe unten). Das heißt,

x	=	Z * sin(ωt-φ) + Y*sin(ωt)
	=	Z * sin(ωt-90) + Y * sin(ωt)
	=	-Z * cos(ωt) + Y * sin(ωt)

Die maximale Verschiebung von x, angegeben als X, entspricht aufgrund des Phasenunterschieds nicht Y + Z. Es kann jedoch gezeigt werden, dass eine andere Form der letzten Gleichung x = X * sin(ωt+ φ) ist, wobei die Größe X = sqrt(Z^2 + Y^2) und φ der Phasenwinkel ist. Daher ist bei Z = 0.745 cm und Y = 0.280 cm die absolute Verschiebung der Masse 0.796 cm.

ANFANG DER LAST 1
Angewendete Frequenz Fall-Nr.	1 (Angewendete Frequenz = 1.985E+00 Hz)
Modus-Nr.	Phasenwinkel (Grad)	Amplitude
1	8.9934E+01	1.1172E+00
Auszug aus der Übersichtsdatei der Frequenzantwort

Schritt 3: Durchführen einer Verlaufsanalyse:

Kehren Sie zur Registerkarte FEM-Editor zurück (Werkzeuge Umgebungen FEM-Editor).
Um die transiente Durchbiegung aufgrund der oszillierenden Basis zu berechnen, stellen Sie die Analyseart ein auf Transiente Spannung (Analyse Änderung Art Linear Transiente Spannung (Modale Überlagerung). Wenn Sie aufgefordert werden, das Modell in ein neues Entwurfsszenario zu kopieren, klicken Sie auf Ja. Die Ergebnisse für die transiente Spannung werden im Entwurfsszenario 3 angezeigt.
Definieren Sie ähnlich wie zuvor die Grundbewegung unterhalb der Analyseparameter ( Setup Modell einrichten Parameter ).
Es ist nicht bekannt, wie viele Zyklen benötigt werden, um von einer Nullbewegung zu fast stationären Zuständen zu gelangen. Wenn wir davon ausgehen, dass es 10 Zyklen dauert, ist eine Dauer von 5 Sekunden ausreichend. [= (10 Zyklen)/( 2 Zyklen/s]. Um die Ergebnisse über einen Sinuszyklus exakt zu erfassen, versuchen Sie den Zyklus in 50 Schritte aufzuteilen. Die Zeitschrittgröße beträgt 1/[ (2 Zyklen/s) * (50 Schritte/Zyklus] = 0.01 Sekunden. Geben Sie die Anzahl der Zeitschritte als 500 und die Zeitschrittgröße als 0.01 ein.
Definieren Sie die Lastkurve für die Basisbewegung. Klicken Sie auf die Lastkurven. Die Lastkurventabelle für Zeit und Faktor müssen ausgefüllt werden. Hier ist der Faktor die Beschleunigung der Basis (in cm/Sek ^ 2). Aus vorherigen Analysen geht hervor, dass die Größe der Grundbeschleunigung 43,55 cm/s ^ 2 beträgt, sodass die Gleichung für die Grundbeschleunigung (43.55 cm/Sek^2)*sin(1.985 Hz * (2pi Radiante/Zyklus) * Zeit) ist. Anstatt die Werte für jeden Zeitschritt einzugeben, können Sie die Berechnung in einer Tabellenkalkulation durchführen, in einer Datei mit kommagetrennten Werten (CSV) speichern und in die Lastkurve laden. Mit dieser Methode wurde eine Datei erstellt, die sich im Unterordner des Models im Installationsordner von Autodesk Simulation befindet. Klicken Sie im Dialogfeld Lastkurveneingabe auf den Import. Klicken Sie auf Durchsuchen, wählen Sie die Datei 43.55sine.csv, und klicken Sie auf Öffnen. In der Anzeige sollte der Inhalt der Datei gezeigt werden. Da die erste Zeile eine Beschriftung zur Identifikation der Daten ist, geben Sie unter Erste überspringen den Wert 1 ein. Klicken Sie auf Importieren, um den Prozess abzuschließen. Die sinusförmige Lastkurve wird angezeigt. Klicken Sie auf OK, um das Dialogfeld Lastkurveneingabe zu schließen.
Geben Sie einen Dämpfungsfaktor (Bruchteil von Kritisch) von 0.188 pro Problemangabe ein.
Die Registerkarte Lasten, auf der Knotenlasten angewendet werden, kann ignoriert werden, da in diesem Beispiel die Grundbeschleunigung verwendet wird. Stellen Sie daher auf der Registerkarte Optionen den Bodenbewegungstyp auf Verformung ein.
Klicken Sie auf Setup, um die Parameter für die Bodenbewegung anzugeben. Stellen Sie als Lastkurve für die Z-Richtung die Option Lastkurve 1 und als Betrag Beschleunigung den Wert 1 cm/s2 ein. (Der Beschleunigungsbetrag wird auf 1 eingestellt, weil die Lastkurve die volle Größe angibt.) Klicken Sie auf OK, um das Dialogfeld Setup Bodenbewegung zu schließen.
Da die transiente Spannungsanalyse die Ergebnisse aus der Modalanalyse verwendet, geben Sie in das Feld Modale Ergebnisse aus Entwurfsszenario verwenden den Wert 1 ein.
Klicken Sie auf OK, um die Analyseparameter zu schließen und das Modell zu analysieren. Klicken Sie auf Analyse Analyse Simulation ausführen.
Wenn die Analyse abgeschlossen ist, wird das Modell in der Ergebnisanzeige angezeigt. Beachten Sie, dass 500 Zeitschritte der Ergebnisse geprüft werden können, ein Schritt pro Berechnungsschritt. Anstatt die Ergebnisse schrittweise zu prüfen, ist es sinnvoll, die Ergebnisse zu plotten.
Legen Sie als Art der Ergebnisse Z-Verschiebung fest (Ergebniskonturen Verschiebung Z).
Wählen Sie den Knoten an der konzentrierten Masse (Auswahl Form Punkt oder Rechteck und Auswahl Auswählen Knoten, und klicken Sie oben im Modell auf den Knoten). Klicken Sie mit der rechten Maustaste, und wählen Sie Graphenwert(e). Es wird ein zweites Präsentationsfenster mit einem Graphen erstellt. Das Ergebnis sollte dem in Abbildung 2 entsprechen. Nach ungefähr fünf Zyklen wird ein fast stationärer Zustand erreicht. Nach visuellen Aspekten scheinen die Ergebnisse ca. 0.75 cm zu sein, die erwartete Verschiebung der Masse relativ zum Lager.
Kehren Sie zum Konturfenster, Präsentation 1 <Unbenannt> zurück, indem Sie in der Strukturansicht auf das Fenster klicken. Ein Zeitschritt von ungefähr 4 Sekunden sollte in Maximalnähe liegen, sodass wir den tatsächlichen Wert der Verschiebung prüfen können. Geben Sie unter Ergebniskonturen Optionen für Lastfall Lastfall Festlegen einen Wert von 400 ein, und klicken Sie auf OK. Bewegen Sie sich einige Zeitschritte vor oder zurück (Ergebniskonturen Optionen für Lastfall Weiter oder Vorige), bis der Schritt mit den maximalen Verschiebung gefunden wird. Schritt 403 weist eine Verschiebung von 0.742 cm auf.

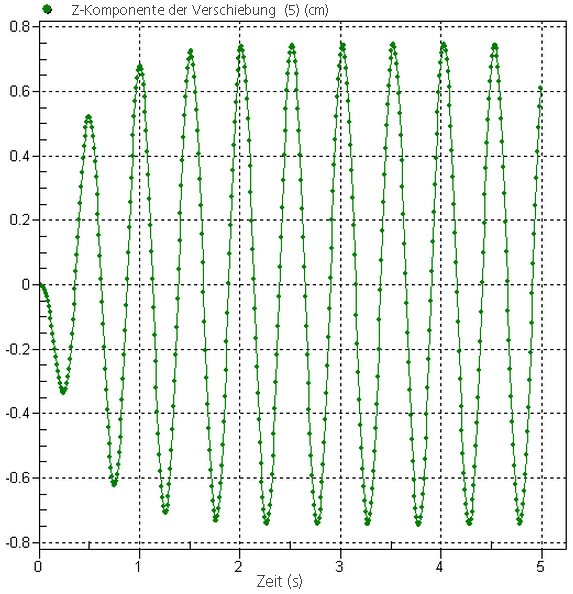
Abbildung 2: Verschiebungsplot von Masse

Ein Archiv des Modells und der Ergebnisse (ground motion.ach) befindet sich im Modellunterverzeichnis des Autodesk Simulation Installationsverzeichnisses.

Dieses Beispiel lässt sich mithilfe der Verfahren aus vielen Fachbüchern über Vibration lösen. Dieses spezielle Beispiel ist nach Beispiel 4-9 aus Vierck, Robert K., Vibration Analysis, Vibration Analysis, Seiten 129-130 angeordnet.