Vorgangsübersicht
Wenn der Leitfähigkeitskoeffizient eine Funktion der Temperatur ist (orthotropes Materialmodell) oder wenn Strahlung auf das Modell angewendet wird, müssen mehrere Iterationen durchgeführt werden, damit die Probleme bei der Analyse der stationären Wärmeübertragung gelöst werden können. Wenn beispielsweise die Temperaturen nicht bekannt sind, ist auch die Wärmeleitfähigkeit nicht bekannt, die Temperaturen können aber ohne die Wärmeleitfähigkeit nicht berechnet werden. Daher ist ein iteratives Verfahren erforderlich.
Verwenden Sie zusätzlich zur temperaturabhängigen Leitfähigkeit und Strahlung für geradlinige Zwecke diese Auswirkungen für die Berechnung der Körper-zu-Körper-Strahlung und der Konvektion als Funktion von Temperatur, wie sie im folgenden Abschnitt beschrieben wird.
Bei jeder Iteration des stationären Solvers werden die temperaturabhängigen Leitfähigkeitskoeffizienten und die Strahlungsraten der Wärmeübertragung anhand der zuvor geschätzten Knotentemperaturen (T i akt) geschätzt. Bei der ersten Iteration werden die Ausgangstemperaturen entweder durch die einzeln auf die Knoten angewendeten Werte (Rechtsklick auf einen Knoten und Auswahl des Befehls Hinzufügen: Temperatur) oder global gegeben (Standardknotentemperatur auf der Registerkarte Optionen im Bildschirm Analyseparameter). Wenn Ausgangstemperaturen für Knoten im FEM-Editor angegeben sind, überschreiben diese Werte die Standardwerte. Das Modell wird dann analysiert. Die resultierenden Temperaturen (Ti neu ) werden mit der früheren Schätzung der Knotentemperaturen verglichen. Wenn der Unterschied zwischen den früheren und den resultierenden Temperaturen akzeptabel ist, wie unten definiert, werden die Analyseiterationen angehalten. Wenn der Unterschied nicht akzeptabel ist, werden Wärmeleitfähigkeits- und Strahlungswärmeraten basierend auf den neuen angenommenen Knotentemperaturschätzungen neu berechnet, und das Problem ist erneut gelöst. Dieser Vorgang wird in Abbildung 1 veranschaulicht.
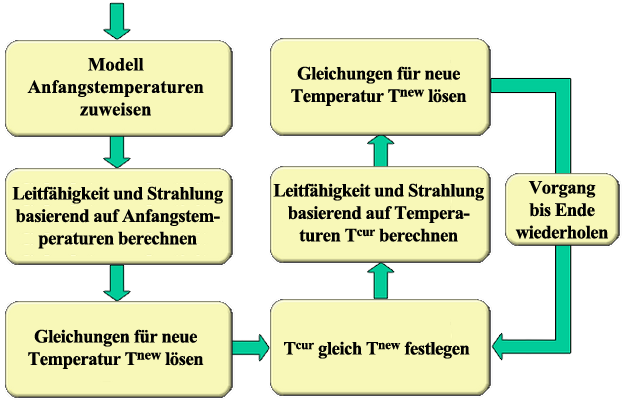
Abbildung 1: Nichtlinearer Lösungsvorgang
In der Realität werden die Temperaturen, mit denen die Leitfähigkeit oder die Strahlung der nächsten Iteration (T akt ) berechnet werden, als [(1-A)(T i alt )+(A)(T i neu )] oder als das Äquivalent [T i alt +A(T i neu -T i alt )] berechnet, wobei A der Relaxationsparameter (festgelegt im Feld Relaxationsparameter auf der Registerkarte Erweitert des Bildschirms Analyseparameter) und T i alt die bei der vorherigen Iteration berechnete Temperatur ist. Ein Wert von 1 wird normalerweise empfohlen. Die angenommenen Temperaturen für die nächste Iteration sind die resultierenden Temperaturen (T i neu ) aus der gerade ausgeführten Iteration. Werte zwischen 0 und 1 werden verwendet, wenn Sie die Temperaturen T akt durch einen kleineren Wert aktualisieren möchten, um mögliche überlange Schwingungen zu dämpfen. Da ein Wert von 0 dazu führen würde, dass die Temperaturen nicht aktualisiert werden, verwenden Sie einen Relaxationsparameter ungleich 0. Ein Relaxationsparameter ungleich 1 wird benötigt, wenn die Knotentemperaturen zwischen aufeinanderfolgenden Iterationen wechseln, anstatt gleichmäßig zu konvergieren.
Die neu angenommenen Temperaturen werden verwendet, um den Leitfähigkeitskoeffizienten zu aktualisieren und die Strahlungsgleichungen neu zu berechnen. Der Vorgang wird wiederholt.
Leitfähigkeit als Funktion von Temperatur
Wenn Sie ein orthotropes Materialmodell verwenden, können Sie die Leitfähigkeit als Funktion von Temperatur angeben. Sie geben die Temperaturwerte entsprechend der Leitfähigkeitswerte an. Die orthotropen Eigenschaften müssen in aufsteigender Reihenfolge der Temperatur angegeben werden. Der in der Lösung zu findende Temperaturbereich darf die obere oder untere Temperaturgrenze, für die Materialeigenschaften bereitgestellt werden, weder unter- noch überschreiten. Leitfähigkeitskoeffizienten werden durch lineare Interpolation zwischen den angegebenen Temperaturwerten berechnet.
Der Vorgabewert für die Ausgangstemperatur ist 0. Bleibt dieser Wert unverändert, muss die minimale angegebene Temperatur zur Bestimmung des Leitfähigkeitskoeffizienten kleiner oder gleich 0 sein. Die Ausgangstemperaturen werden verwendet, um die Leitfähigkeitskoeffizienten zu berechnen. Die zuvor beschriebene nichtlineare Option muss für die Iteration der Temperaturen zum Aktualisieren der Leitfähigkeitskoeffizienten verwendet werden.
Strahlung
Der Wärmestrom (Wärmeübertragung/Zeit/Bereich) bei einer der Strahlung ausgesetzten Fläche wird durch die folgenden Gleichungen definiert:
Dabei gilt:
- q = Wärmestrom
- F rad = Strahlungsfaktor, einschließlich Absorptionsfähigkeit, Emissionsgrad und Sichtfaktor
- σ = Stefan-Boltzmann-Konstante
- X= Strahlungsmultiplikator, der auf dem Bildschirm Analyseparameter angegeben wird
- T s = berechnete Oberflächentemperatur, Einheiten müssen in absoluter Temperatur (Grad Rankine oder Kelvin) angegeben sein
- T rad = Umgebungstemperatur, Einheiten müssen in absoluter Temperatur (Grad Rankine oder Kelvin) angegeben sein
Die Strahlungsparameter F rad und Trad werden auf der Registerkarte Strahlung des Bildschirms Oberflächeneigenschaften angegeben, da sie zu den flächenbasierten Lasten zählen. Die Modelltemperaturen können in Grad F oder Grad C eingegeben werden. Sie werden durch die Eingabe auf der Registerkarte Strahlung auf dem Bildschirm Analyseparameter in absolute Temperaturen umgerechnet. Auf diesem Bildschirm wird auch die Stefan-Boltzmann-Konstante angegeben.
Die Menge (T s 4 -T rad 4 ) kann als (T s 2 +T rad 2 )(T s +T rad )(T s -T rad ) umgeschrieben werden. Wenn die Menge (T s 2 +T rad 2 )(T s +T rad ) als konstant angenommen wird, dann kann ein linearer Lösungsalgorithmus verwendet werden. Die nichtlineare Laufzeitoption ersetzt T i alt durch Ts im Konstantenteil der Gleichung und iteriert wie oben beschrieben. Der Relaxationsparameter (A) muss möglicherweise gesenkt werden, wenn während des Iterationsvorgangs Schwingungen in der Lösung auftreten.
Körper-zu-Körper-Strahlung
Die zuvor erläuterte Strahlungsart gilt für ein Bauteil, das in die Umgebung strahlt. In der Realität übertragen Bauteile häufig Wärme durch Strahlung über andere Flächen desselben Bauteils und anderer Bauteile. Klicken Sie mit der rechten Maustaste in den Anzeigebereich, und wählen Sie den Befehl Körper-zu-Körper-Strahlung, oder wählen Sie Setup
ThermolastenKörper-zu-Körper-Strahlung. Sie können die Oberflächen, die gegenseitig durch Strahlung Wärme aufeinander übertragen, in separate Gehäuse setzen. Sie können die Emissionsvermögen dieser Flächen als konstante Werte oder als temperaturabhängige Werte festlegen. Weitere Informationen finden Sie unter Körper-zu-Körper-Strahlung.
In einigen Fällen kann die Körper-zu-Körper-Strahlung mit temperaturabhängiger Leitfähigkeit emuliert werden (siehe folgende Abbildung):
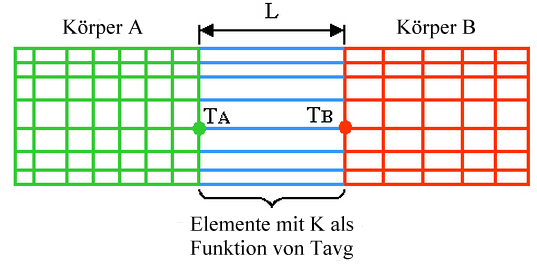
Abbildung 2: Körper-zu-Körper-Strahlung
Die Voraussetzungen für eine genaue Näherung sind wie folgt:
- Der Ansichtsfaktor zwischen den Körpern muss nahe 1 liegen.
- Der Wärmestrom aus dem System heraus ist zu vernachlässigen, d. h., es gibt keine Strahlung in die Umgebung.
- Der Flächenbereich der einzelnen Körper ist gleich.
- Die erwarteten Temperaturen der Oberflächen sind entweder durch manuelle Analysen, Experimente oder vorherige Analysen (mehrere Iterationen) bekannt.
Die zwischen zwei Körpern, die nur Kontakt untereinander haben, ausgetauschte Wärme kann basierend auf dem Oberflächenwiderstand und dem Raumwiderstand der Körper wie folgt beschrieben werden:
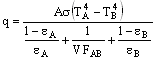
Wenn T A und T B die Temperaturen von Oberfläche A und Oberfläche B sind (in absoluten Temperaturen), sind ε A und ε B die Emissionsvermögen von Oberfläche A und Oberfläche B, und VF AB ist der Ansichtsfaktor zwischen den beiden Oberflächen.
Die Wärmeübertragung aufgrund von Leitfähigkeit zwischen den zwei Körpern ist wie folgt:
Die Wärmeübertragung aufgrund von Strahlung muss gleich der Wärmeübertragung durch Leitung sein. Daher wird die Gleichsetzung der beiden obigen Gleichungen und die Erweiterung von 
wie folgt ausgeführt:
Dies führt zu folgender Lösung:
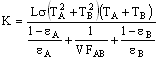
Hierbei sind die Temperaturen absolut.
Eine Elementeschicht wird in einem neuen Bauteil zwischen den beiden Körpern konstruiert. Das Materialmodell wird als orthotrop festgelegt, sodass die Materialeigenschaften temperaturabhängig sind. Die Wärmeleitfähigkeit wird an geschätzten Oberflächentemperaturen T A und T B (absolute Temperatur) mit der obigen Gleichung berechnet. Die berechnete Wärmeleitfähigkeit wird in den Materialeigenschaften bei einer Temperatur von TDurchschnitt = 0.5(T A +T B ) (entweder absolute Temperatur oder die im Dialogfeld Maßeinheitsdefinition festgelegte Temperatur) eingegeben. Zusätzliche Datenpunkte werden durch Auswertung von T Durchschnitt und K bei anderen Werten von T A und T B eingegeben. Achten Sie darauf, dass Sie einen Temperaturbereich T Durchschnitt in den Materialeigenschaften haben, damit die berechnete Temperatur nicht außerhalb des Bereichs der Materialeigenschaften liegt.
- Verwenden Sie für die Körper-zu-Körper-Strahlungsannäherung nur ein Element über die Spanne L. Es darf kein Netz in Richtung L verwendet werden.
- Verschiedene Kombinationen von T A und T B können zu verschiedenen Leitfähigkeiten führen. Dieselbe Temperatur T Durchschnitt , das einzugebende K, sollte ein Durchschnitt aller Leitfähigkeiten sein, die sich für eine gegebene Temperatur T Durchschnitt ergeben.
Thermolasten als Funktion von Temperatur
Konvektions- und Wärmeerzeugungslasten können während der Analyse einer stationären Wärmeübertragung mit der Temperatur variieren. Um eine temperaturabhängige Konvektionslast anzuwenden, aktivieren Sie auf dem Bildschirm Oberflächeneigenschaften auf der Registerkarte Konvektion das Kontrollkästchen Temperaturabhängiger Konvektionskoeffizient. Sie können dann einen Konvektionskoeffizienten im Vergleich zu einer Temperaturkurve definieren, die die Wärmeübertragung über diese Oberfläche aufgrund von Konvektion steuert. Um eine temperaturabhängige Wärmeerzeugungslast anzuwenden, aktivieren Sie in der Elementdefinition auf der Registerkarte Belastung das Kontrollkästchen Temperaturabhängig. Sie können dann eine Wärmeerzeugungsrate im Vergleich zu einer Temperaturkurve definieren, die die Wärmeübertragung durch dieses Bauteil steuert.