Definieren von Lastkurven

Die Informationen auf dieser Seite gelten für die folgenden Analysetypen mit Ausnahme der Stellen, an denen dies gekennzeichnet ist:

Mechanischer Ereignissimulator (MES)

Statische Spannung mit nichtlinearen Materialmodellen

Bei einer Analyse für mechanische Ereignissimulation und statische Spannung mit nichtlinearen Materialien folgt die Mehrzahl der Lasten Lastkurven. Die Lastkurven werden auf der Registerkarte Lastkurven im Dialogfeld Analyseparameter definiert. Hier kann jede beliebige Kurvenform eingegeben werden.

Wählen Sie die Schaltlfläche Nächste Lastkurve hinzufügen oder Lastkurve hinzufügen, um eine weitere Lastkurve hinzuzufügen. Verschiedene Lasten können verschiedenen Lastkurven folgen. So kann z. B. die Schwerkraft in der gesamten Analyse konstant sein und daher einer Lastkurve zugewiesen werden. Eine Kraft kann sinusähnlich variieren, um Exzentrität bei Rotation zu simulieren, und wird daher einer anderen Lastkurve zugewiesen.

Die Lastkurve ist im Abschnitt Daten für ausgewählte Lastkurve durch eine Reihe von Punkten definiert, die ein Idealbild der tatsächlichen Kurve durch eine Reihe gerader Liniensegmente darstellen. Die erste Spalte ist entweder die Zeit oder ein Ergebnis (siehe Details unten), und die übrigen Spalten passen die der Lastkurve zugewiesenen Lasten an, in der Regel durch Multiplikation der Lasten. (Antriebselemente und Zwangsverschiebungen verwenden den Lastkurvenmultiplikator als Änderung der Länge bzw. Drehung, nicht als Multiplikationsfaktor.) Die Kurve wird nach Bedarf linear interpoliert, um den Multiplikator bei der entsprechende Zeit oder dem Ergebnis zu bestimmen.

Verwenden Sie die Schaltfläche Zeile hinzufügen nach Bedarf zum Definieren weiterer Punkte auf der Lastkurve, bzw. die Schaltfläche Zeile löschen zum Entfernen der aktuellen Zeile. Die Lastkurven-Datenpunkte müssen in aufsteigender Reihenfolge nach Zeit oder Ergebnis eingegeben werden. Verwenden Sie die Schaltfläche Sortieren, wenn die Daten anders eingegeben wurden.

Mithilfe der Schaltfläche Lastkurve importieren können Sie auch eine Lastkurve importieren. Erstellen Sie zunächst eine Textdatei in einem kommagetrennten Dateiformat (.csv), in der jede Zeile der Textdatei einer Zeile der Lastkurve entspricht und ein Komma jeden Wert in der Zeile für jede Spalte der Lastkurve trennt. (Die Spalte Index der Lastkurve ist nicht in der Textdatei enthalten.)

Tipp:

• Die Ziellastkurve muss die gleiche Anzahl Spalten wie die CSV-Datei haben. Wenn Sie beispielsweise eine CSV-Datei mit vier Spalten für eine ergebnisbasierte Lastkurve verwenden, können Sie mit den Schaltflächen Lastkurve hinzufügen und Spalte hinzufügen eine leere Lastkurve mit vier Spalten erstellen.
• Die Werte werden unter Verwendung der aktiven Anzeigeeinheiten in die kommagetrennte Datei importiert. Ändern Sie ggf. die Anzeigeeinheiten, bevor Sie die Daten importieren. Beispiel: Ein Wert von 3,14 wird als 3,14 Sekunden importiert, wenn die Anzeigeeinheiten auf Sekunden festgelegt sind, und als 3,14 Minuten, wenn die Anzeigeeinheiten Minuten sind.

Zeitbasierte Lastkurven

Wenn die Last als Funktion der Zeit variiert, wählen Sie Zeit im Abschnitt Daten für ausgewählte Lastkurve aus. Die Lastkurve verfügt über zwei Spalten: Zeit und Multiplikator 1. Geben Sie die Punkte für die Lastkurve direkt in der Laskurventabellenkalkulation ein, oder importieren Sie die Lastkurve (siehe oben).

Beachten Sie, dass die Spalte Zeit der Lastkurve basierend auf den aktiven Anzeigeeinheiten konvertiert wird.

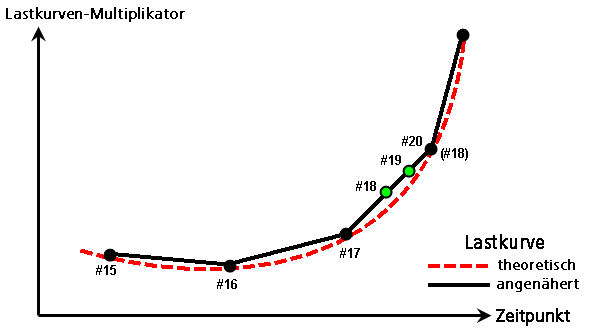
Wenn eine Kurve höherer Ordnung mit einer Reihe gerader Liniensegmente angenähert wird, muss der Abstand der Punkte in der Lastkurve kleiner als der kleinste während der Analyse gefundene Zeitschritt sein. Beispiel: Ein Laufkran beschleunigt um eine bekannte Rate. Dies wird durch Anwendung einer Zwangsverschiebung an der Räderposition simuliert, wo die Verschiebung gegenüber der Zeit d = 0.5*a*t^2. Wenn die Lastkurve berechnet und an den Zeitschritten t basierend auf den Schritten pro Zeit eingegeben wird, dann wird die Kurve genau so lange befolgt, wie die Zeitschritte in der Analyse nie verringert werden. Sobald der Zeitschritt automatisch reduziert wird, um zur Lösung zu konvergieren, wird die Lastkurve interpoliert. Wenn dies eintritt, folgt die Zwangsverschiebung nicht präzise der Beschleunigungsgleichung. Siehe Abbildung 1.

Abbildung 1: Abschnitt einer Lastkurve Zeitschritte Nr. 15, Nr. 16 und Nr. 17 folgen der theoretischen Kurve. Wenn Schritt Nr. 18 konvergieren könnte, befände sich die Last weiterhin auf der theoretischen Kurve (Nr. 18). Wenn jedoch der Zeitschritt reduziert wird, werden die Schritte Nr. 18 und Nr. 19 interpoliert, sodass dies zu einer leicht veränderten Last führt. In vielen Fällen ist der Unterschied zu vernachlässigen (insbesondere in Anbetracht der Annäherungen durch FEM im Allgemeinen).

Ergebnisbasierte Lastkurven

Beispiel: magnetische Kontakte in einer Schaltbaugruppe. Die Kraft, die von der magnetischen Anziehung herrührt, ist keine bekannte Funktion der Zeit, da die Verschiebung des Kontakts (aufgrund anderer Lasten in der Analyse) gegenüber der Zeit unbekannt ist. Die magnetische Kraft variiert je nach der Trennung zwischen den Bauteilen. In dieser Situation definieren Sie eine Lastkurve als Funktion eines Ergebnisses, und während der Analyse wird die Last entsprechend im Verlauf der Zeit variiert.

Bevor Sie das Dialogfeld Analyseparameter zum Definieren einer ergebnisbasierten Lastkurve öffnen, fügen Sie dem Modell Sonden hinzu. Die Sonden befinden sich an den Positionen im Modell, deren Ergebnisse in der Lastkurve verwendet werden. Zum Hinzufügen einer Sonde wählen Sie einen oder mehrere Punkte aus (Auswahl Auswählen Punkte), klicken Sie mit der rechten Maustaste, und wählen Sie Hinzufügen Knotensonde. Ein Dialogfeld wird geöffnet, in dem Sie eine Beschreibung für die Knotensondeobjekte eingeben können. (Siehe Seite Lasten und Abhängigkeiten: Sonden.)

Um festzulegen, dass die Lastkurve auf einem Ergebnis basiert, wählen Sie Suchlaufwert in Daten für ausgewählte Lastkurve aus. Die Lastkurve beginnt dann mit zwei Spalten: Suche und Multiplikator 1. (Zusätzliche Spalten können wie unten beschrieben hinzugefügt werden.) Der Suchlaufwert wird über die Schaltfläche Referenzindizes definieren/bearbeiten definiert. Nach der Definition kann der Suchlaufwert mit dem Pulldown-Menü Suchlaufwert festgelegt werden. Der Name des Suchlaufwerts wird zur Überschrift in der ersten Spalte der Lastkurventabellenkalkulation.

Tipp:

• Zwangsverschiebungen und Antriebselemente können keine ergebnisbasierte Lastkurve verwenden.
• Die erste Spalte der Suchlauf-Lastkurve, die die Ergebnisse der Suchlaufwertgleichung enthält, wird nicht basierend auf den aktiven Anzeigeeinheiten konvertiert. Die Einheiten für den Suchlaufwert und die erste Spalte basieren auf den Modelleinheiten.

Definieren und Bearbeiten von Suchlaufwerten

Durch Klicken auf die Schaltfläche Referenzindizes definieren/bearbeiten wird das Dialogfeld Suchwert definieren geöffnet. Dort werden die Suchlaufwerte basierend auf den Ergebnissen an bestimmten Positionen definiert. Die Funktionen im Dialogfeld Suchwert definieren sind die Folgenden. Sie werden in der Reihenfolge aufgeführt, in der sie normalerweise verwendet werden.

• Klicken Sie auf die Schaltfläche Hinzufügen, um einen neuen Suchlaufwert zu definieren. Der erstellte Suchlaufwert muss einen eindeutigen Namen haben und darf keine Leerzeichen enthalten. Zeit ist ebenfalls kein zulässiger Name, um Verwechslungen mit der Analysezeit zu vermeiden.
• Verwenden Sie das Pulldown-Menü Suchwertname zum Anzeigen der Eingabe für alle zuvor definierten Namen. Nach dem Anzeigen der Eingaben kann jede Eingabe geändert werden. Sie wird gespeichert, wenn Sie zu einem anderen Suchlaufwert wechseln oder auf OK klicken, um das Dialogfeld zu schließen.
• Mit der Schaltfläche Zeile hinzufügen können Sie zusätzliche Zeilen in die Variablentabellenkalkulation einfügen. Die Variablen, die in der Tabellenkalkulation definiert sind, werden in der Gleichung verwendet, die definiert, welches Ergebnis dem Suchlaufwert zugeordnet ist. Jede hinzugefügte Variable erhält automatisch den Namen V1, V2, usw. Der Name einer Variablen kann in einen aussagekräftigeren Namen geändert werden, indem Sie in der Tabellenkalkulation auf den Namen klicken.
• In der Tabellenkalkulation wählen Sie eine Sonde und ein Ergebnis für die einzelnen Variablen aus den Pulldown-Menüs aus. Nur Sonden, die dem Modell hinzugefügt wurden, stehen für die Variablendefinition zur Verfügung. Folgende Ergebnisse können an den Sonden verwendet werden:
  • X-Verschiebung
  • Y-Verschiebung
  • Z-Verschiebung
  • X-Geschwindigkeit
  • Y-Geschwindigkeit
  • Z-Geschwindigkeit
• Im Textfeld Gleichung werden die in der Tabellenkalkulation beschriebenen Variablen zur Definition des Suchlaufwertnamens kombiniert. (Andere Suchlaufwerte können nicht in der Gleichung enthalten sein.) Wenn beispielsweise das Ergebnis einfach die Y-Verschiebung eines Knotens ist, lautet die Gleichung V1, wobei V1 als Y-Verschiebung an der entsprechenden Sonde definiert ist. Wenn der Suchlaufwertname der Durchschnitt dreier Knoten sein soll, dann lautet die Gleichung (V1+V2+V3)/3. Die folgenden Operatoren können in der Gleichung verwendet werden:

  Operator	Bezeichnung
  (und)	Klammern zum Gruppieren von Operationen.
  oder	Exponentfunktion, oder potenziert eine Zahl. Beispiel: V1^2 ergibt das Quadrat der Variablen V1.
  *	Multiplikation.
  /	Division.
  +	Addition.
  -	Subtraktion oder negatives Vorzeichen vor einer Zahl wie z. B. V1-V2, or -V1*5.
  cos( )	Kosinus des Werts in Klammern. Der Wert muss in Radianten angegeben werden.
  sin( )	Sinus des Werts in Klammern. Der Wert muss in Radianten angegeben werden.
  tan( )	Tangens des Werts in Klammern. Der Wert muss in Radianten angegeben werden.
  exp( )	Natürliche Exponentialfunktion des Werts in Klammern, oder Potenzieren von e, z. B. e V1 .
  log( )	Natürlicher Logarithmus des Werts in Klammern, oder Logarithmus der Basis e, in der Mathematik häufig als ln () geschrieben.
  abs( )	Der absolute Wert des Werts in Klammern.
  sqrt( )	Quadratwurzel des Werts in Klammern.
  acos( )	Umgekehrte Kosinusfunktion des Werts in Klammern, bzw. Arkuskosinus.
  asin( )	Umgekehrte Sinusfunktion des Werts in Klammern, bzw. Arkussinus.
  atan( )	Umgekehrte Tangensfunktion des Werts in Klammern, bzw. Arkustangens.
  cosh( )	Hyperbelkosinus des Werts in Klammern.
  sinh( )	Hyperbelsinus des Werts in Klammern.
  tanh( )	Hyperbeltangens des Werts in Klammern.
  log10( )	Logarithmus der Basis 10 des Werts in Klammern, in der Mathematik oft als log() geschrieben.

Bedingungsanweisungen und Multiplikatoren für mehrere Lastkurven

Wie bislang beschrieben, wird der für die Lastkurve ausgewählte Suchlaufwert ein einzelner Wert, der zum Bestimmen des Multiplikators der Last verwendet wird - ebenso wie die Zeit der einzelne Wert in einer zeitbasierten Lastkurve ist, mit dem der Lastmultiplikator bestimmt wird. Es gibt Situationen, in denen mehrere Ergebnisse oder mehrere Suchlaufwerte sind Werte sich auf die Größe der Last auswirken. In diesen Fällen wird das Textfeld Bedingung zusammen mit mehreren Spalten in der Tabellenkalkulation verwendet, um zu bestimmen, welche Multiplikatorspalte basierend auf dem ausgewählten Suchlaufwert interpoliert wird.

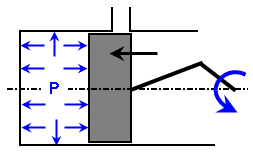
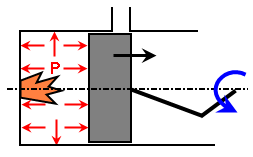
Beispiel: Ein Zweitaktmotor, wie schematisch in Abbildung 2 dargestellt. Beachten Sie, dass die Position des Kolben in Abbildung 2 und in Abbildung 2b die Gleiche ist. Der Druck in Abbildung 2a basiert aber auf dem Zuleitungsdruck und der Bewegung des Kolbens, da der Auspuffanschluss verschlossen wurde (Gaskompression), während der Druck in Abbildung 2b auf dem Verbrennungsdruck und der Bewegung des Kolbens seit der Verbrennung (Gasexpansion) beruht. Daher kann die Lastkurve nicht auf der Kolbenposition basieren, jedoch auf der Kolbenposition und Geschwindigkeit. Diese Art von Steuerelement wird ermittelt, indem das Textfeld Bedingung verwendet wird. Das Format ist Folgendes:

IF (Suchlaufwert-Testvergleich; Multiplikatorspalte falls wahr, Multiplikatorspalte falls falsch)

Dabei gilt:

• Der Suchlaufwert ist ein vorhandener Suchlaufwertname, der über Referenzindizes definieren/bearbeiten erstellt und definiert wurde.
• Test ist eines der folgenden bedingten Symbole:

  Symbol	Bezeichnung
  >= oder =>	größer oder gleich
  <= oder =<	kleiner oder gleich
  =	gleich
  >	größer als
  <	kleiner als

• Vergleich ist ein numerischer Wert. Es kann sich nicht um einen anderen Suchlaufwert handeln. Um einen Suchlaufwert wie z. B. Vel1>Vel2 zu verwenden, definieren Sie einen neuen Suchlaufwert Vel3 = Vel1 - Vel2, und verwenden Sie den Vergleichstest Vel3>0.
• Multiplikatorspalte wenn wahr ist eine Zahl, die angibt, welche Multiplikatorspalte von der Lastkurve verwendet werden soll, wenn der Vergleichstest wahr ist.
• Multiplikatorspalte wenn falsch ist eine Zahl, die angibt, welche Multiplikatorspalte von der Lastkurve verwendet werden soll, wenn der Vergleichstest falsch ist.

Beachten Sie, dass das Semikolon (;) verwendet wird, um die drei Teile der IF-Bedingung zu trennen.

(a) Die Zuleitungsgase werden komprimiert.	(b) Die Verbrennungsgase dehnen sich aus.
Abbildung 2: Zweitaktkolben Obwohl die Position des Kolben in beiden Fällen gleich ist, ist der Druck P unterschiedlich.

Basierend auf dem Ergebnis des Bedingungstests wird die entsprechende Spalte aus der Lastkurventabellenkalkulation interpoliert. Verwenden Sie die Schaltflächen Spalte hinzufügen und Spalte löschen zum Hinzufügen oder Entfernen von Multiplikatorspalten aus der Tabellenkalkulation. Wenn keine Bedingungsanweisung verwendet wird (das Bedingungstextfeld ist leer), dann wird nur die Spalte Multiplikator 1 verwendet, unabhängig davon, wie viele Spalten in der Tabellenkalkulation eingegeben werden.

Tipp:

• Die Bedingungsgleichung kann verschachtelt werden, sodass Typvorgänge einbezogen werden können. Beispiel: Die folgende Anweisung wird aufgeschlüsselt: IF(sep1<10;3;IF(vel>0;1;2)). Wenn das Ergebnis, das durch die Variable sep1 definiert wird, kleiner als 10 ist, dann wird die Multiplikatorspalte 3 verwendet (wahre Bedingung). Wenn sep1 nicht kleiner als 10 ist (falsche Bedingung), dann ist die Multiplikatorspalte für die falsche Bedingung ein anderer Test, der ausgewertet werden muss - wenn das von der Variablen vel definierte Ergebnis größer 0 ist, dann wird der Multiplikator in Multiplikatorspalte 1 verwendet; wenn vel nicht größer 0 ist, wird die Multiplikatorspalte 2 verwendet. Zusammenfassend gilt:
  • Die Multiplikatorspalte 3 wird verwendet, wenn sep1 kleiner als 10 ist.
  • Die Multiplikatorspalte 1 wird verwendet, wenn sep1 größer oder gleich 10 und vel größer als 0 ist.
  • Die Multiplikatorspalte 2 wird verwendet, wenn sep1 größer oder gleich 10 und vel kleiner oder gleich 0 ist.

Beispiel 1: Magnetische Kräfte

Bei dem Beispiel für magnetische Kraft in Abbildung 3 wird von den folgenden Parametern ausgegangen:

• X = 0,5 Zoll in der Ruheposition (vor dem Aktivieren der Magneten)
• F = 0,3125/(S^2) nach dem Aktivieren des Magneten, wobei S die tatsächliche Trennung ist

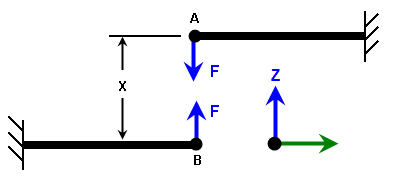
Abbildung 3: Beispiel für magnetische Anziehung

Die Schritte zum Einrichten der magnetischen Kräfte sind Folgende:

1. Wählen Sie den oberen Knoten A aus (Auswahl Auswählen Punkte), und wenden Sie eine Knotenkraft an (Rechtsklick auf Hinzufügen Knotenkraft). Legen Sie die Größe der Kraft auf -1 und die Richtung auf die Z-Achse fest. Durch Verwendung einer Einheitskraft entspricht der Lastkurvenmultiplikator der gesamten magnetischen Kraft. Klicken Sie auf die Schaltfläche OK zum Anwenden der Kraft.
2. Fügen Sie bei ausgewähltem Knoten eine Sonde hinzu (klicken Sie mit der rechten Maustaste). Geben Sie eine Beschreibung für den oberen Knoten ein, und klicken Sie auf die Schaltfläche OK.
3. Wählen Sie den unteren Knoten B aus (Auswahl Auswählen Punkte), und wenden Sie eine Knotenkraft an (Rechtsklick auf Hinzufügen Knotenkraft). Legen Sie die Größe der Kraft auf +1 und die Richtung auf die Z-Achse fest. Klicken Sie auf die Schaltfläche OK zum Anwenden der Kraft.
4. Fügen Sie bei ausgewähltem Knoten eine Sonde hinzu (Rechtsklick auf Hinzufügen Knotensonde). Geben Sie eine Beschreibung für den unteren Knoten ein, und klicken Sie auf die Schaltfläche OK.
5. Öffnen Sie das Dialogfeld Analyseparameter (Analyse: Parameter), und wählen Sie das Optionsfeld zum Festlegen des Lastkurventyps auf Suchlaufwert. Die erste Spalte der Lastkurventabellenkalkulation wechselt von Zeit zu Suchlaufwert.
6. Definieren Sie eine neue Variable, die für den berechneten Abstand zwischen den beiden Magneten steht. Klicken Sie auf die Schaltfläche Referenzindizes definieren/bearbeiten. Es wird ein neues Dialogfeld geöffnet. Klicken Sie auf Hinzufügen, und geben Sie den neuen Variablennamen Separation (Trennung) ein. Klicken Sie auf OK, um den Eintrag des Suchlaufwertnamens abzuschließen und zum Dialogfeld Suchwert definieren zurückzukehren.
7. Die Trennung ist eine Gleichung, die auf der Verschiebung zweier Knoten basiert. Klicken Sie daher einmal auf die Schaltfläche Zeile hinzufügen, um eine zweite Variable, V2, zur Tabellenkalkulation hinzuzufügen.
8. Wählen Sie für die Variable V1 die Sonde Oberster Knoten und das Ergebnis von Z-Verschiebung.
9. Wählen Sie für die Variable V2 die Sonde Unterster Knoten und das Ergebnis von Z-Verschiebung.
10. Die Gleichung für die berechneten Trennung wird dann in das Textfeld Gleichung eingegeben. Geben Sie 0.5+V1-V2 ein. Beachten Sie, dass eine positive Verschiebung des oberen Knotens diese Trennung erhöht; daher wird V1 zur anfänglichen Trennung von 0,5 hinzugefügt. Eine positive Verschiebung des unteren Knotens verringert die Trennung; daher wird V2 von der anfänglichen Trennung von 0,5 abgezogen.
11. Klicken Sie auf OK, um das Dialogfeld Suchwert definieren zu schließen.
12. Verwenden Sie im Hauptdialogfeld Analyseparameter das Pulldown-Menü Suchwert, und wählen Sie Separation als Suchlaufwert aus. Die erste Spalte der Lastkurventabellenkalkulation ändert sich von Suchwert zu Getrennt.
13. Abschließend bewerten Sie den Multiplikator (in diesem Fall die magnetische Kraft) bei verschiedenen Trennungen, und geben Sie diese in die Lastkurventabellenkalkulation ein. Bei einer Trennung von 0 ist die Kraft zwar theoretisch unendlich. Die folgende Lastkurve ist jedoch vom FEM-Gesichtspunkt aus praktischer - dabei ist Kontakt erforderlich, um die Bauteile vom gegenseitigen Durchdringen abzuhalten. Daher sollte die Trennung die Größe 0 nicht erreichen. Beachten Sie die zusätzlichen Einträge für eine Trennung größer als 0,5 (die anfängliche Trennung). Die Lastkurve sollte alle möglichen Trennungsbereiche abdecken für den Fall, dass die Objekte vibrieren oder durch andere Lasten weiter als um die anfängliche Trennung getrennt werden.

    Index	Separation	Multiplikator 1
    1	0	100
    2	0,1	31.25
    3	0,2	7.81
    4	0.3	3.47
    5	0.4	1.95
    6	0.5	1.25
    7	0.6	0.868
    8	0.7	0.638
    9	0.8	0.488

14. Klicken Sie auf die Schaltfläche Kurve anzeigen, um zu bestätigen, dass die Form wie erwartet hyperbolisch ist. Es scheinen mehr Datenpunkte zwischen 0 und 0,2 benötigt zu werden, um eine glattere Kurve zu erhalten.

Beispiel 2: Zweitaktkolben

Für den Zweitaktkolben aus den Abbildungen 2 und 4 werden die folgenden (erfundenen) Parameter angenommen:

• X = -1,25 Zoll (X-Verschiebung des Kolbens, wenn der Auspuffanschluss vollständig verschlossen ist)
• Kompressionstakt = 1,5 Zoll (X0 = -1.5)
• Bohrung = 3 Zoll Durchmesser
• V0 = 14,2 Zoll^3 = Volumen der eingeschlossenen Luft, wenn der Auspuffanschluss geschlossen ist
• Zuleitungsdruck = 10 psig
• Verbrennungsdruck = 1000 psig
• Jeder Takt ist ein isothermischer Prozess; der Gasdruck kann nach dem idealen Gasgesetz berechnet werden.
• Das Volumen der eingeschlossenen Luft zwischen dem Kolben und dem Zylinderkopf wird anhand des Abstands genähert, um den sich der Kolben von X0 bewegt hat. Die Volumenänderung durch die Erweiterung der Zylinderbohrung wird an dieser Stelle ignoriert.

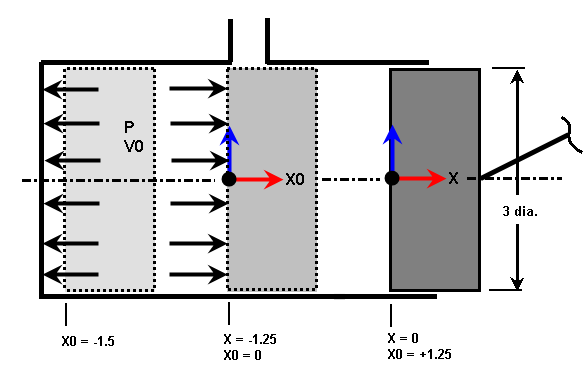
Abbildung 4: Beispiel Zweitaktkolben

Der Kolben wird in drei Positionen gezeigt. X = 0 ist die Position, an der das Modell gezeichnet wird. X0=0, wenn der Auspuffanschluss verschlossen wird, sodass die eingeschlossenen Gase ein Volumen V0 und einen Druck haben. X0=-1,5 ist die Vorwärtsposition des Kolbens.

Natürlich können die auf die Lastkurve angewandten Drücke komplizierter als das ideale Gasgesetz sein, um die Komprimierbarkeit und Wärmeverluste zu berücksichtigen. Zudem behandelt dieser Aufbau nur den Druck am Zylinderkopf und der blinden Seite des Kolbens. Es ist eine zusätzliche Bearbeitung erforderlich, um den Druck auf den Seiten der Zylinderwände und am Stangenende des Kolbens einzuschließen. Diese Drücke folgen einer anderen ergebnisbasierten Lastkurve.

1. Wählen Sie die Flächen (Auswahl Auswählen Flächen) am blinden Ende des Kolbens und am Zylinderkopf aus, und wenden Sie einen Einheitsdruck von 1 psi an (Rechtsklick und Hinzufügen Flächendruck/-zug). Aktivieren Sie das Kontrollkästchen Der Verschiebung folgen, und klicken Sie auf OK, um den Druck anzuwenden.
2. Wenn der Hub des Zylinderkopfes ignoriert wird, kann das Volumen der eingeschlossenen Luft nur anhand der Kolbenposition berechnet werden. Wählen Sie einen Knoten auf dem Kolben aus (Auswahl Auswählen Punkte), klicken Sie mit der rechten Maustaste, und wählen Sie Hinzufügen: Knotensonde. Geben Sie eine Beschreibung des Kolbens ein, und klicken Sie auf OK, um die Sonde hinzuzufügen.
3. Öffnen Sie das Dialogfeld Analyseparameter (Analyse: Parameter), und wählen Sie das Optionsfeld zum Festlegen des Lastkurventyps auf Suchlaufwert. Die erste Spalte der Lastkurventabellenkalkulation wechselt von Zeit zu Suchlaufwert.
4. Definieren Sie eine neue Variable, die die Position des Kolbens gegenüber dem Auspuffanschluss angibt, bzw. die Position X0 in Abbildung 4. Klicken Sie auf die Schaltfläche Referenzindizes definieren/bearbeiten. Es wird ein neues Dialogfeld geöffnet. Klicken Sie auf Hinzufügen, und geben Sie den neuen Variablennamen X0 ein. Klicken Sie auf OK, um den Eintrag des Suchlaufwertnamens abzuschließen und zum Dialogfeld Suchwert definieren zurückzukehren.
5. Wählen Sie für die Variable V1 die Sonde Kolben und das Ergebnis von X-Verschiebung.
6. Die Gleichung für die Kolbenposition gegenüber dem Auspuffanschluss X0 wird dann in das Textfeld Gleichung eingegeben. Geben Sie V1+1.25 ein.
7. Definieren Sie eine neue Variable, die für die Geschwindigkeit des Kolbens steht. Klicken Sie auf Hinzufügen, und geben Sie den neuen Variablennamen Velocity (Geschwindigkeit) ein. Klicken Sie auf OK, um den Eintrag des Suchlaufwertnamens abzuschließen und zum Dialogfeld Suchwert definieren definieren zurückzukehren.
8. Wählen Sie für die Variable V1 die Sonde Kolben und das Ergebnis von X-Geschwindigkeit. Beachten Sie, dass die gleiche Sonde für mehrere Suchlaufwerte verwendet wird. Die Variable V1 des Suchlaufwerts X0 ist auch völlig unabhängig von der Variablen V1 in der Suchlaufwertvariablen Velocity (Geschwindigkeit).
9. Die Gleichung für die Kolbengeschwindigkeit ist einfach die Variable V1. Geben Sie V1 in das Textfeld Gleichung ein, und klicken Sie auf OK, um das Dialogfeld Suchwert definieren zu schließen.
10. Verwenden Sie im Hauptdialogfeld Analyseparameter das Pulldown-Menü Suchlaufwert, und wählen Sie X0 als Suchlaufwert aus. Die erste Spalte der Lastkurventabellenkalkulation ändert sich von Suchlaufwert zu X0.
11. Wie oben beschrieben, ist in dieser Analyse eine auf Geschwindigkeit basierende Bedingung erforderlich. Geben Sie den Text IF(Velocity>0;1;2) in das Textfeld Bedingung ein. Wenn die Geschwindigkeit positiv ist (der Kolben bewegt sich nach rechts), dann dehnen sich die Verbrennungsgase aus, und die Multiplikatorspalte 1 wird verwendet. Wenn die Geschwindigkeit negativ ist (der Kolben bewegt sich nach links), dann werden die Verbrennungsgase komprimiert, und die Multiplikatorspalte 2 wird verwendet.
12. Klicken Sie auf die Schaltfläche Spalte hinzufügen, um eine zweite Multiplikatorspalte in der Lastkurventabellenkalkulation hinzuzufügen.
13. Schließlich können Sie die Multiplikatoren (der Druck in diesem Beispiel) an verschiedenen Positionen der Kolben bewerten und sie in die Lastkurve eingeben. Anhand des idealen Gasgesetzes kann der Druck Pc für den Kompressionstakt (-1.5<=X0<=0) aus dem anfänglichen Druck Psupply und Volumen Vinitial wie folgt berechnet werden:

    Pinitial*Vinitial = P*V

    Psupply*V0 = P*(V0+X0*(pi/4)*Bohrung^2)

    (10 psig + 14.7 psi)*(14.2 Zoll^3) = (Pc+14.7 psi)*(14.2 Zoll^3+7.0686*X0)

    Pc = 350.74/(14.2+7.0686*X0) - 14.7

    Für den Ausdehnungstakt kann der Überdruck Pe wie folgt berechnet werden:

    Pinitial*Vinitial = P*V

    Pcombustion*(V0 - (Takt)*(pi/4)*Bohrung^2) = P*(V0+X0*(pi/4)*Bohrung^2)

    (1000 psig + 14.7 psi)*(14.2 Zoll^3-10.60 Zoll^3) = (Pe+14.7 psi)*(14.2 Zoll^3+7.0686*X0)

    Pe = 3652.92/(14.2+7.0686*X0) - 14.7

    Index	X0	Multiplikator 1 (ausdehnende Gase, Pe)	Multiplikator 2 (komprimierende Gase, Pc)
    1	-1.75	1981	177
    2	-1.5	1000	82.8
    3	-1.25	666	50.7
    4	-1.0	498	34.5
    5	-0.5	328	18.2
    6	0	243	10
    7	0,1	10	10
    8	10	10	10

Beachten Sie die allmähliche Druckänderung, während der Auspuffanschluss geöffnet wird (0<X0<0.1). Zudem wird der Kolben theoretisch nie an die Positionen -1.5<X0 verschoben; es ist jedoch etwas Vorlauf für Rundungen und Hub des Systems erforderlich. Daher wird die Lastkurve für einen Takt von -1.75 berechnet.

Übergeordnetes Thema: Analyseparameter