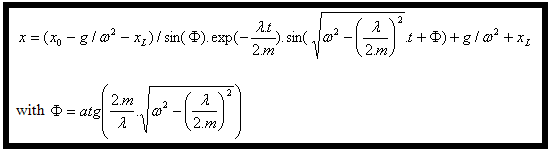One of the steps in responsible design process is validation. To validate a design it is often good to use simple reliable theoretical cases to measure against. The following are such cases.
These cases describe the equations and assumptions used in achieving the validation of a simulation output.
Displacement, the Mass-Spring Case
A simple mass and spring validation case.

Newton’s law:
![]() (1)
(1)
With:
| Numerical value: | |
|---|---|
| |
|
| |
|
| |
|
| |
10 |
| |
20 |
| |
15000 |
| |
0.3 |
| |
9.81 |
| |
0.33 |
| |
0.0 |
|
(1) |
|
|
with |
|
|
|
|
|
A solution for this differential equation is: |
|
|
|
|
|
A particular solution, when the system is stabilized, is for |
|
|
Then (2) |
|
|
|
|
|
|
|
|
The initial conditions give the value of A and |
|
|
for t = 0.0, (3) |
|
|
|
|
|
and |
|
|
|
|
|
Finally, (4) and (6) reported in (3) gives the equation of the displacement : |
|
|
|
|
|
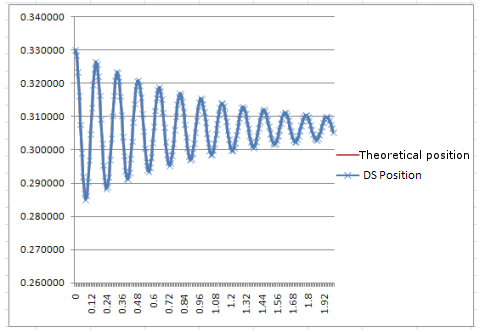
This equation was then programmed in Excel and the results compared with the results produced by Dynamic Simulation, the results being identical. |
|
 |
|
Position and Velocity, the Crank-Piston Case
The purpose of this validation case is to check the position and velocity in a crankshaft and piston mechanism when output from dynamic simulation in comparison with theoretical equations describing the same.
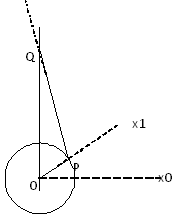
Known values: The “throw” or distance of the crankshaft journal from the rotational center of the crankshaft, and the length of the connecting rod between the main bearing journal and the piston pin joint.
Diagram
|
Definition |
R = length(OP) = crankshaft throw L = length(PQ) = connecting rod length |
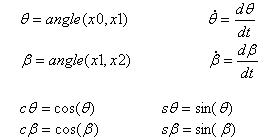 |
|
|
Velocity of point Q in relation to the absolute coordinate system R0 = (x0, y0) |
|
|
|
// position of Q in R0 |
|
|
//velocity of Q in R0 |
| with:
|
|
| and:
|
|
|
|
|
| with: |
|
| and; |
|
| then: |
|
|
Point Q stays on the y0 axis and the x0 component is 0.0 : |
|
|
|
|
 |
|
| Finally, using (1): | |
|
|
|
|
Equation (1) gives |
|
|
(1) |
|
and 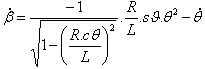 |
|
| Using MS Excel and numerical values (L=0.125m, R=0.06m, and |
|
|
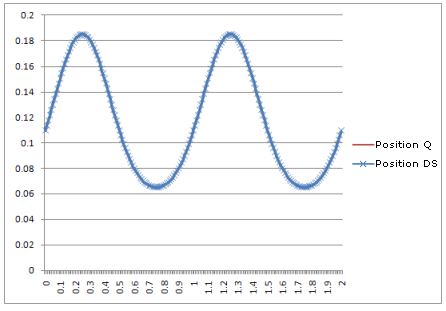
Position: |
|
 |
|
|
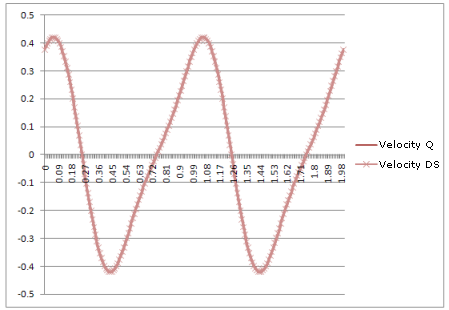
Velocity: |
|
 |
|
The result: curves in dynamic simulation are identical to the curves produced by the theoretical equations.
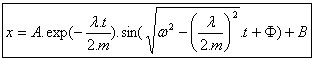 (3)
(3)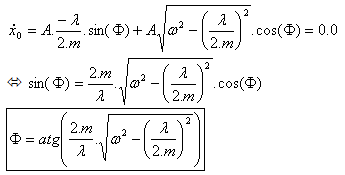 (5)
(5)