
Sheet metal parts are defined by their folded or functional state, but are fabricated from a flat sheet. The bends that are unfolded to form the flat pattern deform the material within the bending zone. The amount of deformation depends on some variables. Transforming the folded model to the flattened state requires accounting for this deformation using one of three methods:
- a linear approximation using a defined KFactor
- measured values captured in a bend table for specific materials, bend angle values and tooling
- custom equations that provide uniform deformation within specified angular bounding conditions
Use custom equations to specify exactly how you want to account for the flattening of the bend zones within your folded sheet metal part models. These custom equations are defined within a named unfold rule that is defined using the Style and Standard Editor dialog box.
The equation types for solving the flattened deformation are further described in the following sections.
Bend Compensation Type
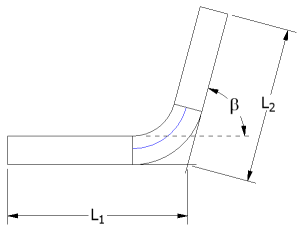
The bend compensation equation allows you to determine the total developed length using the equation:
where:
|
|
is the total developed length. |
|
|
is the length from the first detail face to the virtual sharp. |
|
|
is the length from the second detail face to the virtual sharp. |
|
|
is the result of the bend allowance calculation. |
Inventor calculates a bending allowance using the following equations. For angular cases:
the equation used is:
where:
|
|
is the bend angle. |
|
|
is the bend allowance length. |
|
|
is the bend plate inner radius. |
|
|
is the sheet thickness. |
|
|
is the result of the bend allowance calculation. |
Expanding the original equation to include the bend allowance calculation results in:
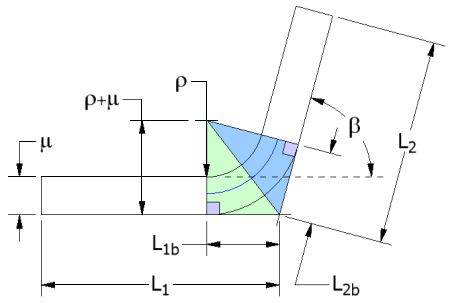
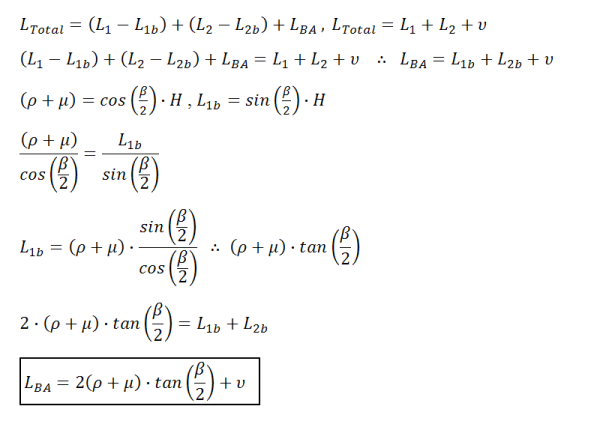
For angular cases:

The following equation is used:
Expanding the original equation to include the bend allowance calculation results in:
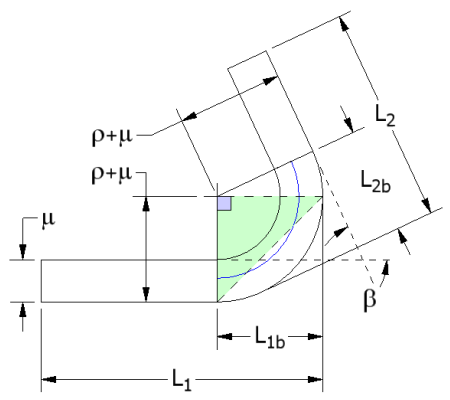
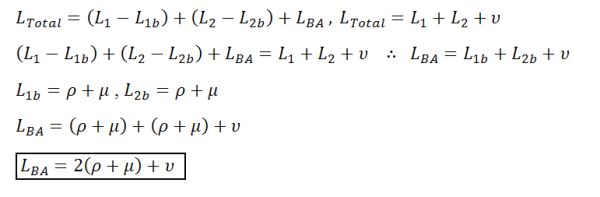
Once the bend allowance has been determined the KFactor can be derived using:
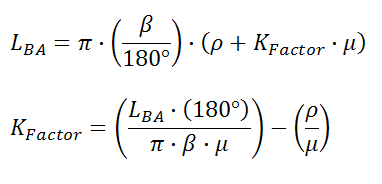
Bend Deduction Type

The bend deduction equation allows you to determine the total developed length using the equation:
where:
|
|
is the total developed length. |
|
|
is the length from the first detail face to the virtual sharp. |
|
|
is the length from the second detail face to the virtual sharp. |
|
|
is the result of the bend allowance calculation. |
The bend deduction equation provides a calculation method which can be thought of as the direct opposite of the bend compensation method.
For bend deductions, Inventor calculates a bending allowance using the following equations. For angular cases:
the equation used is:
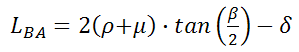
where:
|
|
is the bend angle. |
|
|
is the bend allowance length. |
|
|
is the bend plate inner radius. |
|
|
is the sheet thickness. |
|
|
is the result of the bend allowance calculation. |
For angular cases:
the equation used is:
Bend Allowance Type
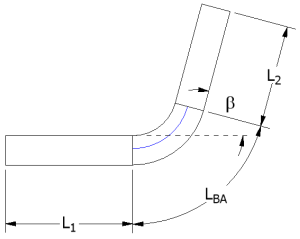
The bend allowance equation allows you to determine the total developed length using the equation:
where:
|
|
is the total developed length. |
|
|
is the length of the first bend plate. |
|
|
is the length of the second bend plate. |
|
|
is the result of the bend allowance calculation. |
A defined equation is supplied to solve for the bend allowance directly. The KFactor can be derived from the following equation:
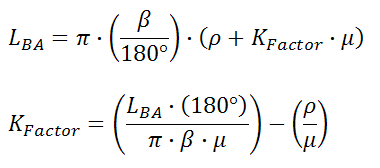
KFactor Type
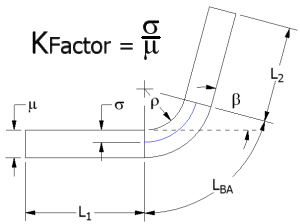
Determining the total developed length using the KFactor method uses the equation:
where:
|
|
is the total developed length. |
|
|
is the length of the first bend plate. |
|
|
is the length of the second bend plate. |
|
|
is the result of the bend allowance calculation. |
The bend allowance is calculated using the following equation: