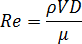Coolant viscosity model

The viscosity, flow rate, and Reynolds number of a coolant are interrelated.

The coolant viscosity model is given by the following equation: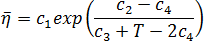

where:

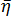• is the viscosity (Pa.sec.)
• is the coolant temperature (K)
• is a data-fitted coefficent (Pa.sec)
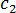• , and 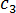are data-fitted coefficients (K)
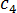• is equivalent to 273.15 K

Relationship between flow rate, Reynolds number, and viscosity

The relationship between flow rate and viscosity can be derived from the theory of incompressible viscous flow through pipes, beginning with the Darcy-Weisbach formula: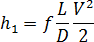

where:

• is the head loss, which is equivalent to 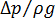, the pressure drop in the pipe divided by the density of the fluid times the gravity constant
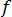• is the friction factor
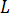• is the length of the pipe
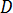• is the diameter of the pipe
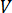• is the average flow velocity, which is equivalent to 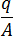, the flow rate divided by the cross-sectional area of the pipe

Substituting for and 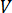as above, we get: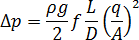

The friction factor, 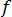, in the above equation is related to the Reynolds number, 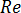, as follows for lower Reynolds numbers where :

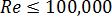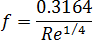
For the higher range, where the Reynolds number is given by 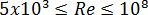, the friction factor is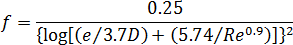

where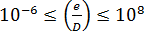

The Reynolds number is related to the viscosity, 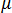, by the following equation: