Coolant flow behaviour affects heat transfer between the mold and coolant. Heat transfer effectiveness is increased when the coolant flow is turbulent and not laminar. Turbulent coolant flow has a better temperature gradient than laminar flow.
- The temperature gradient across the metal, which depends on the conductivity of the metal
- The temperature gradient across the coolant and metal interface, which depends on coolant flow
The heat flow path from plastic to cooling channel
The speed of coolant flow can affect the heat transfer.
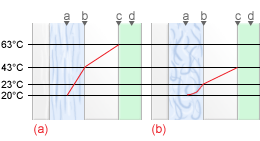
At very low speeds the flow is laminar; the heat has to be conducted through various layers of coolant to the center of the channel. Since coolant is a poor conductor of heat, heat transfer is very inefficient. This is shown in the following graph a below where there is a relatively large temperature difference between the coolant metal interface and the center of the channel.
As coolant flow increases, heat transfer increases at a marginal rate until the coolant flow becomes turbulent. There is now a component of coolant velocity perpendicular to the channel which causes a dramatic improvement in heat transfer. The greater heat transfer shown in following graph b results in a lower temperature at the cavity wall for coolants with a turbulent flow.
In these graphs, the mold elements are represented by the following:- a - Coolant
- b - Water/metal interface
- c - Cavity wall
- d - Plastic part
Laminar and turbulent flow
The relationship between heat transfer and coolant flow can be expressed as a power factor. Coolant flow is either laminar or turbulent, or in transition between laminar and turbulent. For laminar flow, heat transfer increases proportional to the cube root of the flow rate.
This means that doubling the coolant flow increases the heat transfer by about 24 percent. For fully turbulent flow, the heat transfer is proportional to the square of the cube root of the flow rate. Therefore, in the turbulent zone, doubling the coolant flow increases heat transfer by 59 percent.
The power required to pump coolant around the system is proportional to the flow rate cubed. This means that doubling the coolant flow will require eight times the pumping power.
When turbulent flow has been fully developed, greater increases in flow rate will increase the molds capacity to extract heat. However, the amount of heat that can be extracted is limited by the amount of heat passing into the mold, and heat extraction may not be improved beyond this limitation.
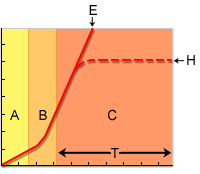
The most effective condition for heat transfer is to ensure that coolant flow is turbulent, and the capacity to extract heat does not greatly exceed the amount of heat available for extraction. The following graph shows heat extraction from the mold as a function of the coolant flow rate. In region A heat transfer is by conduction, in region C heat transfer is by convection, while B is a region transition. The solid line, E, reflects the heat extraction capacity; the dotted line, H, indicates the actual heat extraction.
Reynolds number
The Reynolds number is a ratio that defines the rate of fluid flow in pipes. The onset of turbulence in water is between 2300-4000. The Reynolds number is assigned to cooling circuits when the flow rate is not known. A Reynolds number of 4000 is considered fully turbulent, but it is good practice to use a Reynolds number of 10,000 to represent turbulent flow when running an analysis.
Cooling system equations have more information about the Reynolds Number.