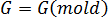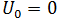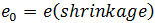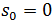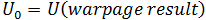Initial conditions analysis (Concept)

This Stress analysis is based on the deflected part determined from Warp analysis.

We call this "Initial Conditions Analysis". The analysis uses both the deflections and the shrinkage strains determined from the Warp analysis, as a starting point for the Stress analysis.

Initial conditions analysis is available for each of the three analysis types described in the preceding sections. In this section, we first describe how the Warp results are passed to the Stress analysis, then present some discussion on how the initial conditions analysis should be used in conjunction with the main analysis types. These include: small deflection, buckling, large deflection and modal frequency analyses.

If we write:

= model geometry
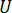= displacements 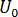= initial displacements
= strains 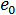= initial strains
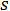= stress 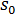= initial stress

then we can compare the inputs to warpage and initial conditions Stress analysis as follows:

Warp analysis:

Initial conditions Stress analysis:

The key point to note in the above is that initial stresses are not used to carry through the "residual stresses from warpage". Instead, they are carried through by virtue of 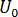and 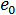. On the very first step of a Stress analysis, FENAS effectively duplicates the stress calculation that was done at the last step of the Warp analysis. There is no overhead in this because stresses are always calculated at the beginning of a large deflection analysis.

The alternative (simplistic) approach is to pass the warped shape

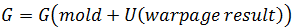
and initial stresses, 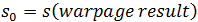to the initial conditions stress analysis.

The method used, as described above, achieves the same effect but has the following advantages:

A consistent strain definition (strain=deformation/length) is used in both analyses because the geometry data ( ) doesn't change. To illustrate this, a warped part was subjected to zero load. The adopted method predicted zero response-there was no movement. This is not the case with the initial stress approach because of the change in strain definition, that is there is an "artificial redistribution" of stresses to cope with the change of definition.
You can easily scale down the residual stresses from the Warp analysis, by reducing the elastic moduli in the stress analysis. Reduced elastic moduli can be used in the stress analysis to simulate roughly the effect of relaxation of the residual stresses from warpage, and to allow for creep under load (an "effective linear modulus" can be used)).

For example, if for warpage you use E1=1600 and E2=1200 MPa, and for external-loading you use E1=800 and E2=600 MPa, then the stress computed at the start of the first step of the external-loading analysis is half of the residual stress output at the end of Warp analysis. You can therefore pass "reduced residual stresses" through into the external-loading analysis. This would not be as easy to do with the initial stress approach.
Post-processing is simplified because there is no need to add initial stresses to the stresses from the structural or Warp analysis, to produce the final stress.

Initial Conditions and the Three Analysis Types

This section includes some specific comments on using initial conditions analysis with each of the analysis types.

Buckling Analysis

When a buckling analysis is run, two analyses are performed; a small deflection analysis followed by a buckling analysis.

Generally, the linear (classical) buckling method is used. The initial small deflection analysis is used to determine the part configuration at 100% load. The buckling analysis then uses the known configurations at 0 and 100% load. When post-processing the results, you can examine the deflected shape at 100% load, as well as the mode shape(s) determined from the buckling analysis.

For buckling analysis with initial conditions however, the classical linear buckling theory can not be applied to the problem because the stresses are non-zero before the load is applied. The "Linearized Buckling" Method must therefore be used. In this method, the initial small deflection analysis is used to determine the part configuration at a very small percentage of the load. The linearized buckling analysis then uses the known configurations at 0% and at the end of the small step.

Note: This means that when post-processing initial conditions buckling analysis results, the deflected shape at 100% load is not available. You can only display mode shapes.

If you need the linear result, you will need to run a small deflection analysis as well as the buckling analysis.

Since the mode shape determined from the buckling analysis is an incremental mode shape (the change in configurations at the buckling point), it must be superimposed on the warped shape (after suitable scaling).

Large Deflection Analysis

Note: The large deflection initial conditions stress analysis should only be performed on large deflection warpage results.

Large deflection Warp analysis results can only be used if the warpage response is known to be highly linear, that is if the eigenvalues from a buckling analysis are very high.

Modal Frequency Analysis

Modal frequency analysis may also use the initial conditions from Warp analysis. Similar comments to those for buckling analysis apply in this case.

Effect of Including Initial Conditions

The stresses from warpage may have a stabilizing or destabilizing effect on the response of the part under load. For example, if the residual stresses cause compression of a slender surface, then this effectively adds to the stress caused by a compressive load. An analysis which does not include initial conditions would over predict the failure load in this case.

Alternatively, if the warpage stresses cause tension, then a compressive load might balance out the residual stress, so that an analysis not including initial conditions would give a too conservative prediction of the failure load.

Prescribed Displacements and Initial Conditions

A useful feature of the software is the ability to prescribe displacements (rather than apply loads) in an initial conditions analysis. This allows you to determine the force(s) required to deform the warped shape into a known configuration. The final result will also show the stresses caused by forcing the part into that configuration.

For each node to which a prescribed displacement boundary condition has been applied, FENAS will output the "reaction force" in the results summary file.

Can Stress Results be used as Initial Conditions?

The following two examples illustrate when it might be useful to prepare an initial conditions analysis based on a Stress analysis:

A warped part has been forced into shape using a prescribed displacement Stress analysis. You then want to find the response of that part to further external loading.
External loading has been applied to a part. You then want to find the response of the part to thermal loading.

In this release however, you cannot use structural results as initial conditions for another Stress analysis, for the following reason.

Warp analysis results can be used as initial conditions for the Stress analysis because the constraint reactions from the Warp analysis are close to zero. For an externally loaded Stress analysis, in which the constraint reactions are all non-zero, it is necessary to pass these reactions to the second analysis. If these reactions are not passed, equilibrium requirements may be violated, particularly if the constraints were moved.

In this release, there is no mechanism to pass the constraint reactions from the first analysis to the second. For this reason, the Stress analysis program will not allow you to use a Stress analysis result file as initial conditions.