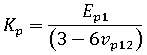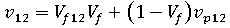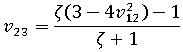Fiber orientation is one of the major factors that determines the mechanical (elastic) strength as well as the stiffness of a molded part.
Theories have been developed to predict the mechanical properties of short fiber composites once the fiber orientation distribution in the parts is known.
To calculate the mechanical properties, all the theories follow a two step procedure:
- The properties of a unidirectional short fiber reinforced material are estimated.
- These properties are then averaged across the laminates according to the fiber orientation distribution density.
Thus, this methodology independently accounts for the influence of fiber length and fiber orientation.
The Tandon-Weng model serves as the basis for the calculation of the composite material's unidirectional mechanical properties. The Autodesk Simulation Moldflow Insight implementation also considers Tucker/Liang's treatment on the Poisson ratio calculation of the Tandon-Weng model.
The properties of the fiber and polymer required as inputs to the analysis are:
-
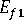 (longitudinal modulus of fiber)
(longitudinal modulus of fiber) -
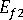 (transverse modulus of fiber)
(transverse modulus of fiber) -
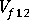 (longitudinal Poisson's ratio of fiber)
(longitudinal Poisson's ratio of fiber) -
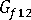 (longitudinal shear modulus of fiber)
(longitudinal shear modulus of fiber) -
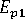 (longitudinal modulus of polymer)
(longitudinal modulus of polymer) -
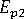 (transverse modulus of polymer)
(transverse modulus of polymer) -
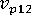 (longitudinal Poisson's ratio of polymer)
(longitudinal Poisson's ratio of polymer) -
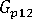 (longitudinal shear modulus of polymer)
(longitudinal shear modulus of polymer) -
 (average fiber length)
(average fiber length) -
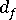 (average fiber diameter)
(average fiber diameter) -
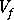 (volume fraction of fibers)
(volume fraction of fibers)
The following basic mechanical properties are derived for each element in the composite material:
-
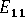 (longitudinal modulus)
(longitudinal modulus) -
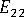 (transverse modulus)
(transverse modulus) -
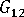 (in-plane shear modulus)
(in-plane shear modulus) -
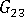 (out-of-plane shear modulus)
(out-of-plane shear modulus) -
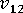 (in-plane Poisson's ratio)
(in-plane Poisson's ratio) -
 (out-of-of-plane Poisson's ratio)
(out-of-of-plane Poisson's ratio)
Longitudinal and transverse moduli
The Tandon Weng model treats the short fiber reinforced composite as a special case of unidirectionally aligned spheroidal inclusions embedded in a finite elastic polymer matrix.
The longitudinal modulus of the uniaxially aligned system can be written as:
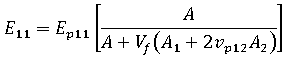
where 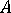 ,
, 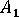 and
and 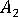 are parameters related to those in the Tandon Weng paper.
are parameters related to those in the Tandon Weng paper.
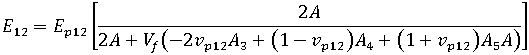
where 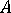 ,
, 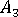 ,
, 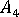 and
and 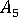 are parameters related to those in the Tandon Weng paper.
are parameters related to those in the Tandon Weng paper.
Shear modulus and Poisson's ratio
The Halpin-Tsai procedures are applied when calculating the longitudinal and transverse shear moduli and Poisson's ratios for the composite material.
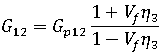
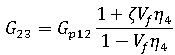
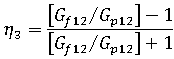

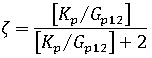
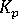 is the bulk modulus of the polymer, defined as
is the bulk modulus of the polymer, defined as