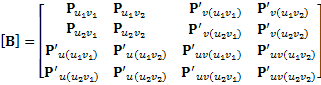Mathematical representation of face types
This section describes the face types encountered in Revit geometry, their properties, and their mathematical representations.
PlanarFace
A plane defined by origin and unit vectors in U and V. Its parametric equation is
CylindricalFace
A face defined by extruding a circle along an axis. The Revit API provides the following properties:
- The origin of the face.
- The axis of extrusion.
- The “radius vectors” in X and Y. These vectors are the circle’s unit vectors multiplied by the radius of the circle. Note that the unit vectors may represent either a right handed or left handed control frame.
The parametric equation for this face is:
ConicalFace
A face defined by rotation of a line about an axis. The Revit API provides the following properties:
- The origin of the face.
- The axis of the cone.
- The “radius vectors” in X and Y. These vectors are the unit vectors multiplied by the radius of the circle formed by the revolution. Note that the unit vectors may represent either a right handed or left handed control frame.
- The half angle of the face.
The parametric equation for this face is:
RevolvedFace
A face defined by rotation of an arbitrary curve about an axis. The Revit API provides the following properties:
- The origin of the face
- The axis of the face
- The profile curve
- The unit vectors for the rotated curve (incorrectly called “Radius”)
The parametric equation for this face is:
RuledFace
A ruled surface is created by sweeping a line between two profile curves or between a curve and a point. The Revit API provides the curve(s) and point(s) as properties.
The parametric equation for this surface is:
if both curves are valid. If one of the curves is replaced with a point, the equations simplify to one of:
A ruled face with no curves and two points is degenerate and will not be returned.
HermiteFace
A cubic Hermite spline face. The Revit API provides:
- Arrays of the u and v parameters for the spline interpolation points
- An array of the 3D points at each node (the array is organized in increasing u, then increasing v)
- An array of the tangent vectors at each node
- An array of the twist vectors at each node
The parametric representation of this surface, between nodes (u1, v1) and (u2, v2) is:
Where ![]() ,
, ![]() , MH is the Hermite matrix:
, MH is the Hermite matrix:
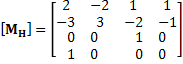
And B is coefficient matrix obtained from the face properties at the interpolation points: