Loads applied to bars acting on some eccentricity let you define forces applied to a bar in a distance to a longitudinal bar axis. Eccentricity (force distance to a longitudinal bar axis) is defined in a local coordinate system of a bar. This option is available by clicking Load on eccentricity, which is found in dialogs that define uniform load and bar force (moment) applied along the length of a bar.
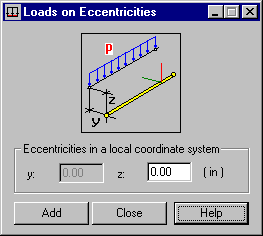
The previous dialog defines load eccentricity for a uniform load. A similar dialog is opened for a force acting along a bar length. Loads on eccentricity can be defined for the following types of loads:
- Concentrated force and moment acting in the point on the bar length (bar force)
- Uniform load on a bar.
|
Concentrated force and moment on a bar length |
Uniform load |
|---|---|
|
Field y: Distance value of the point of force applied in a local y direction Field z: Value of the distance of the point of force applied in a local z direction Default values of point distance (y=z=0.0) are accepted when the y and z fields are empty Accepted unit: Currently-used for section dimensions |
Field y: Distance value of the point of a uniform load applied in a local y direction Field z: Value of the distance of the point of force applied in a local z direction Default values of point distance (y=z=0.0) are accepted when the y and z fields are empty. Accepted unit: Currently-used for section dimensions. |
Load generation
Loads defined on eccentricity are reduced to a bar axis. Load generation for a general 3D case is shown in the following image.
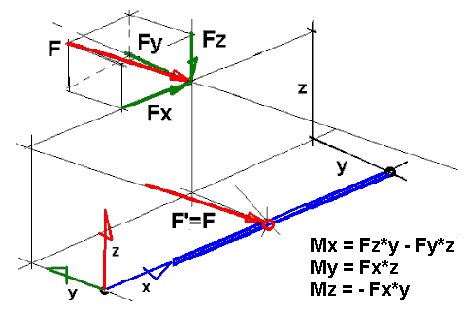
The following applies to loads on eccentricity:
- A concentrated moment defined on an eccentricity does not generate any additional loads.
- A concentrated force defined with a distance to a bar axis is moved to the x
0
application point with the same F force value and direction of action. Also, concentrated moments applied to an x
0
point are generated. Concentrated force components (in relation to the local element coordinate system) Fx, Fy, Fz are found. Next, additional moments in a local system can be calculated.
Mx = Fz*y - Fy*z
My = Fx*z
Mz = - Fx*y
- A uniform load defined on an eccentricity is applied to the whole length with the same p load value and direction of action. Also, a uniform moment load is generated along the whole length of a bar. As for concentrated forces, when uniform load components px, py, and pz are found, a uniform load should be generated:
mx = pz*y - py*z
my = px*z
mz = - px*y.
- For 2D structures (FRAME 2D, TRUSS 2D), an eccentricity is defined only in the z direction. Field y is not accessible in a dialog at that time. As a general rule for 2D structures, loads in a local system are not rotated with a gamma angle. The same rule applies to the eccentricity direction of loads. to Only My moments are generated.
- For 2D structures (PLATE and GRILLAGE) type, an eccentricity is defined in a y and z direction. As a general rule for 2D structures, loads in a local system are not rotated with a gamma angle. The same applies to the eccentricity direction of loads. Only Mx= Fz*y - 0*z moments are generated.