The radiation model supports geometric symmetry. Symmetric divisions must be such that the model is a true fraction of the complete model. For example, a half symmetric model is valid if the other half makes up the complete device. Likewise, a quarter symmetry is valid if it encompasses 90 degrees of the actual device, and if the other three quarters would make up the complete device.
A slip condition that does not divide a model along a geometry symmetry would not produce accurate radiative heat transfer results. Examples of valid symmetry/slip divisions are shown:

These two examples show valid half and quarter symmetry geometries, but much smaller symmetry can be used, if it is valid. As an example, an 18 degree wedge could be analyzed from a disk. This corresponds to a 1/20th symmetry! The key is to apply the symmetry (slip) boundary conditions so that they properly define the symmetry.
When working with a symmetric model, care should be taken to ensure that the model uses pure rotational symmetry. A combination of rotational and mirrored symmetry is not supported. For example, if the complete geometry looks like the image on the left, then a valid quarter symmetry would be as shown on the right:
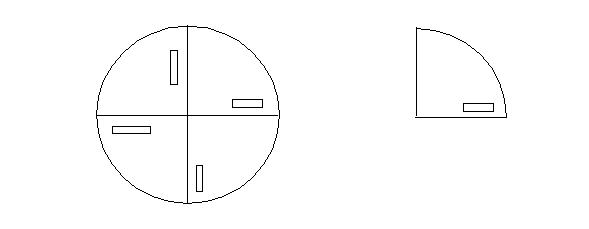
But, if the actual geometry did not contain pure rotational symmetry, and looked like the image on the left (below), then the symmetry shown in the middle image would be wrong. The image on the right is the correct way to invoke symmetry on such a model:

To properly model symmetry, it must be possible to rotate the symmetric model through 360 degrees and arrive at the original geometry. This is to ensure that the effects of shadowing and reflection are accurately accounted for by the radiation model.
The radiation model also supports 2D axisymmetric models. Such models must be axisymmetric about either the x or y axis.
Rotational Periodic symmetry is also supported by the radiation model. The wedge angle must be at least three degrees, and periodic faces are marked using the periodic boundary conditions on the Loads dialog. Translational periodic symmetry, however, is not supported.