The following paragraphs present definitions of some of the mathematical terms that are associated with solving CFD equations.
Linear - Non-linear
The governing equations are listed in the next section. In these equations, two types of non-linearities appear. The first kind of non-linearity is exemplified by the advection terms. For example, in the u velocity equation, there appears a term:

So in these terms, u depends on the product of u and its derivative. The second of type of non- linearity that appears in the governing equations is that the properties or factors of the terms depend upon the dependent variable. For example, the density in the energy equation depends upon the temperature, for which the equation is solved. Also, the eddy viscosity used for turbulent flows for the diffusion terms in the velocity equations is highly dependent upon the velocities. These two types of non-linearities are by far the predominant influences on the numerical solution. For this reason, the equations must be solved in an iterative manner.
Explicit - Implicit
If a term is treated implicitly, it becomes part of the coefficient matrix and thus part of the solution. If it is treated explicitly, then previous iterates’ values are used instead of the most current information. These terms are usually part of the source term or the load vector. They are determined after the current iteration’s solution. For numerical stability, it is best to treat as many terms implicitly as possible.
For transient analyses, an implicit discretization method is used. This implies that the value at the current time is dependent on the neighboring values at the current time. An explicit discretization method implies that the value at the current time is dependent on the neighboring values from the previous time. An implicit formulation is unconditionally stable numerically - it will yield a solution regardless of the size of the time step. However, it requires an iterative solution within each time step. An explicit formulation is only conditionally stable numerically. It is highly dependent and frequently highly restrictive in terms of time step size. It is not unheard of to use time steps of 1.E-10 seconds for explicit formulations. However, you do not need to iterate the solution inside each time step.
Symmetric - Non-Symmetric
The governing partial differential equations in the next section are discretized, using finite elements, into a set of algebraic equations with the unknowns being nodal values of the solution variables. These algebraic equations can be written in matrix form as:
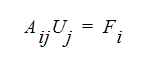
where Fi is the load vector, Uj is the unknown vector and Aij is the coefficient matrix. For a symmetric system of equations, the upper diagonals of A are a mirror image of the lower diagonals, i.e.,

For non-symmetric systems, this is not true. In general, second order derivative terms (e.g., diffusion terms) will produce symmetric matrices and first order derivatives (advection terms) produce non-symmetric matrices.