Fluid Flow Definitions

Incompressible - Compressible

The term compressible refers to the relationship between density and pressure. If a flow is compressible, changes in fluid pressure affect its density and vice versa. Compressible flows involve gases at very high speeds.

One major difference between compressible and incompressible flow is seen in both the physical nature of pressure and consequently, the mathematical character of the pressure equation. For incompressible flow, downstream effects are felt everywhere immediately and the pressure equation is mathematically elliptic, requiring downstream boundary conditions. For compressible flow, particularly supersonic flows, downstream pressure cannot affect anything upstream and the pressure equation is hyperbolic, requiring only upstream boundary conditions.

Downstream boundaries must be left free of pressure constraints.

Mach Number

One measure of compressibility is the Mach number, defined as the fluid velocity divided by the speed of sound, defined as:

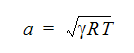
where a is the speed of sound, gamma is the ratio of the specific heats, R is the Universal Gas Constant and T is the static temperature. For Mach numbers less than 0.3, flows can be assumed to be incompressible. Above this value, compressible effects are becoming more influential and must be considered for accurate solutions.

Adiabatic Compressible

If there are no heat transfer effects and the fluid is moving below sonic velocities (Mach = 1.0), the flow can be considered adiabatic. For this type of flow, total energy is conserved. That is, the sum of kinetic and thermal energy is a constant. In equation form, this can be expressed as:

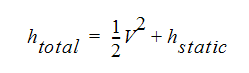
where V is the velocity, and h is the volumetric enthalpy, a measure of energy. Assuming an ideal gas, this equation can be written using temperature:

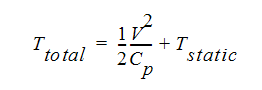
where Cp is the mechanical specific heat value calculated using:

where 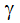is the ratio of the constant pressure specific heat to the constant volume specific heat and Rgas is the gas constant for this gas. The total temperature is also called the stagnation temperature. The first term on the right hand side of this equation is referred to as the dynamic temperature.

Transonic, Supersonic and Hypersonic Flow

These 3 terms are classifications of compressible flow. Transonic flow is at or near sonic velocities. Supersonic refers to the Mach number range: 1<Ma<5. Flows with Mach numbers greater than 5 are called hypersonic. Transonic and supersonic flows can be modeled using the Ideal Gas assumption:

Hypersonic flows cannot be modeled using the Ideal Gas assumption and must consider real gas effects.

Absolute, Total, Static and Dynamic Values

The term absolute is used in conjunction with pressure. Normally, the solution to the pressure equation is a relative pressure. This relative pressure does not contain the gravitational head or the rotational head or the reference pressure. It is the part of the pressure that is affected by the velocities in the momentum equation directly. The absolute pressure adds the gravitational and rotational heads and the reference pressure to that calculated from the pressure equation. Referring to the relative pressure as Prel, the absolute pressure is calculated as:

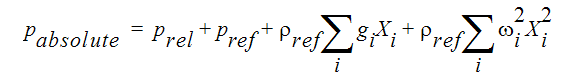
where the ref subscript refers to reference values, the subscript i refers to the 3 coordinate directions, g is the gravitational acceleration and is the rotational speed. The reference density is calculated at the beginning of the analysis using the reference pressure and temperature. For flows with a constant density, the reference density is the constant value. For flows which have no gravitational or rotational heads, the relative pressure is the gage pressure.

The terms dynamic and static are used most commonly with compressible fluids. The dynamic values are kinetic energy-like terms:

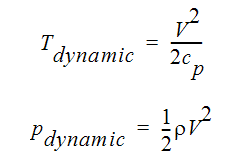
Note that the specific heat used to calculate the dynamic temperature is not the thermal value entered on the property window, but is a mechanical value calculated using:

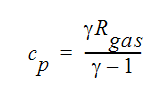
where 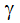is the ratio of the constant pressure specific heat to the constant volume specific heat and R_gas is the gas constant for this gas.

The static temperature is determined by solving the energy equation. For adiabatic properties, the energy equation that is used to determine the static temperature is the constant total temperature equation. Hence, the static temperature is the total or stagnation temperature minus the dynamic temperature.

The static pressure is the absolute pressure shown earlier. The total temperature is the sum of the static and dynamic temperatures. The total pressure is the sum of the static or absolute pressure and the dynamic pressure.

Laminar - Turbulent

Laminar flow is characterized by smooth, steady fluid motion. Turbulent flow is fluctuating and agitated motion. The measure of whether a flow is laminar or turbulent is the speed of the fluid. Laminar flow is typically much slower than turbulent flow. The dimensionless number which is used to classify a flow as either laminar or turbulent is the Reynolds number defined as:

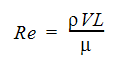
where 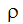is the density, V is the velocity and is the viscosity. For Reynolds numbers greater than ~2500, the flow exhibits turbulent flow phenomena. Most engineering flows are turbulent.

Between the laminar and turbulent flow regimes is the transitional flow regime. In this flow regime, the flow goes through several stages of non-linear behavior before it becomes fully turbulent. These stages are highly unstable, the flow can rapidly change from one type of behavior (turbulent spots, e.g.) to another (vortex breakdown, e.g.) and back again. Due to the unstable nature of this type of flow, it is difficult to numerically predict.

Inviscid - Viscous Flow

Flows for which viscosity or shear effects are neglected are called inviscid. Viscous flows include viscosity or shear effects. All fluids have viscosity. However, there are a limited number of applications where shear effects can be neglected and meaningful results can be obtained.

Inviscid flows are a class of ideal flows which are solved using Euler equations. These equations are a subset of the Navier-Stokes equations. Some compressible flow codes solve the Euler equations instead of the Navier-Stokes. The Euler equations are numerically easier to solve because the mathematical character of the equations never changes. If you include viscous effects, then the solution domain contains areas where elliptic effects dominate and also areas where hyperbolic effects dominate. This is a much more challenging problem.

If the inviscid flow is also irrotational, then you can define a velocity potential function to represent the flow. Such flow is called potential flow. This type of flow is numerically easier still than solving Euler equations, because a single equation can be solved to determine all of the flow parameters. The assumptions of inviscid and irrotational are extremely limiting. However, potential flow solutions can offer some information regarding flow patterns for a very restricted class of fluid flow problems.

Boundary Layer Flow

As a fluid flows over a rigid surface, a boundary layer forms. This boundary layer grows as you move along the surface. The fluid shear is largely contained in the boundary layer. Boundary layer flow refers to a class of fluid flow problems which are primarily concerned with the growth of this shear layer. The boundary layer flow may be next to a surface or a jet wake type flow.

For most boundary layer flows, the pressure in the boundary layer is virtually constant. Outside the boundary layer, the pressure gradient can be varying wildly and this will affect the boundary layer flow. This type of flow is characterized mathematically as parabolic since information is essentially one-way, along the direction of boundary layer growth.

Newtonian or Non-Newtonian Fluid

A Newtonian fluid is one which exhibits a linear relationship between fluid shear and strain:

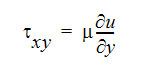
where 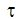is the fluid shear stress, the velocity gradient represents one component of the strain rate tensor and is the coefficient of viscosity. For Newtonian fluids, the viscosity is either constant or a function of temperature. For non-Newtonian fluids, the shear stress is a non-linear function of the strain rate because the viscosity is also a function of the strain rate:

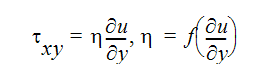
For a non-Newtonian power law fluid, the shear stress is written as:

where m is the consistency index and n is the power law index. In terms of viscosity, this equation can be written:

where 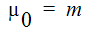and p = n - 1

A Herschel-Buckley non-Newtonian fluid can be described as:

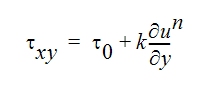
In terms of viscosity, this can be written as:

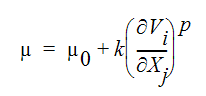
Another non-Newtonian fluid representation is a Carreau model fluid:

Most engineering flows are Newtonian (air, water, oil, steam,.). Fluids which are considered non-Newtonian include: plastic, blood, slurries, rubber and paper pulp.

Conduction, Convection, Conjugate and Radiation Heat Transfer

There are three modes by which heat can be transferred. In conduction, heat is transferred via molecular motion. The heat transfer rate is dependent upon the thermal conductivity. Convection heat transfer refers to heat being transported by fluid motion. Radiation heat transfer is an electromagnetic phenomena which is dependent upon the optical conditions of the radiating media. Conjugate heat transfer refers to the combination of 2 or all 3 of these modes of heat transfer.

Surface-To-Surface Radiation

For most engineering applications, radiant energy interchange occurs from one solid surface to another. The gas contained by the solids is generally non-participatory. The exception to this rule is if the gas is burning or heated as in a furnace. The surface-to-surface radiant interchange will affect the surface temperatures and hence the gas temperatures via convection and conduction. To include radiant interchange in the governing equations, an additional heat flux term, q_ri is added to the wall surface elements. This term is calculated from:

where q_ri is the net heat flux to the fluid at element i from surface-to-surface radiation. G_i is the incident radiation on the face of element i and J_i is the radiosity of element face i. The radiosity can be written as:

where 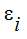is the emissivity and 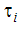is the transmissivity of element surface i and E_bi

is the black body emissive power of element surface i:

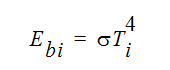
where 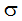is the Stefan-Boltzman constant. The incident radiation can be calculated from:

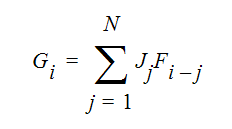
where F_i=j is the view factor between element surface i and element surface j. So the calculation of the radiant heat flux requires the calculation of view factors between all of the element surfaces.

Autodesk Simulation CFD uses two innovative approaches to calculating the view factors. In the first method and older method (Radiation Model 1), a hybrid ray-tracing/discrete ordinates model is used. In this model, we consider a hemisphere surrounding each external element face. The hemisphere is divided into a number of discrete rays. Autodesk Simulation CFD searches these rays to find which other element faces the rays will hit and divide the radiant exchange over these faces. This division is effectively the view factor between the external faces.

In the second and newer method (Radiation Model 4), Autodesk Simulation CFD projects an image of the surrounding element faces onto a sphere surrounding the element face being considered. In effect, this creates a bit map of the surroundings onto this sphere. From this projection, Autodesk Simulation CFD can calculate the exact view factors. In this case, the view factors are as accurate as the pixel resolution of the bit map. As a second step in this method, Autodesk Simulation CFD ensures reciprocity of the view factors:

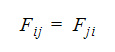
This enforcement of the reciprocity of the view factors does, in turn enforce a radiant energy balance that is very strict. While this method is more accurate than the first method, it does require (at least temporarily) more memory and more CPU time to calculate the view factors. However, this calculation is done once and saved for continuous analysis restarts.

Another feature of Radiation Model 4, is that the view factor calculation allows Autodesk Simulation CFD to include a solar radiant heat flux. To include solar radiation, a dome over the body being analyzed represents the sky. The view factors between this sky dome and the body determine the solar loading on the body. The solar heat flux is calculated automatically by Autodesk Simulation CFD according to the time of day, latitude and longitude.

Natural, Mixed, and Forced Convection

These terms refer to the type of heat transfer. In natural convection, fluid motion is generated or at least dominated by temperature differences which affect the fluid properties, most notably the density. These flows are also referred to as buoyant-driven flows because the gravity term or buoyancy term in the momentum equations dominates the flow. Conversely, in forced convection flows, the temperature is dominated by the fluid motion and buoyancy or gravity has little or no effect. Mixed convection is a combination of these two, where fluid motion and buoyancy may both play a role. Natural convection frequently has no openings or no clearly defined inlets. Forced convection always has inlet region(s) and outlet region(s), as does mixed convection. Free convection is an un-enclosed or open natural convection problem.

In Autodesk Simulation CFD, we do not use the Boussinesq approximation which assumes a constant density in the governing equations. Instead, we use the low Mach number assumption to decompose the pressure:

where P_ref is a constant reference pressure (usually, atmospheric pressure), is a reference density (density at the reference pressure and temperature), g_i is the gravitational vector and x_i is the distance vector from the origin. With this equation substituted into the momentum equations, the new dependent variable becomes the p*. With the static head (second term on the right-hand side) subtracted, the numerical stability is greatly improved.

Convection problems may be laminar or turbulent. For forced convection and most mixed convection problems, the Reynolds number is again the measure for determining flow regimes. For natural convection flows, the Grashof number is the measure. The Grashof number is defined as:

where is the volumetric expansion coefficient, g is the gravitational acceleration, L is a characteristic length, T is the temperature and is kinematic viscosity. Sometimes, the Rayleigh number, which is combination of the Grashof and Prandtl numbers, is also referenced.

The Prandtl number is defined as:

The Rayleigh number is defined as:

where C_p is the constant pressure specific heat, is the absolute viscosity, 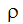is the density and k is the thermal conductivity.

Film Coefficients

Autodesk Simulation CFD calculates film coefficients (convection) in one of two ways. The first way is to calculate the heat transfer residual. The heat transfer residual is calculated by forming the energy equation and substituting the last temperature (or enthalpy values) solution into the formed equations. The residual is the amount of heat required to maintain the solution temperature.

The heat transfer residual is used to determine the film coefficient from the relation:

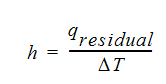
where the temperature difference is that between the wall value and a near wall value.

The second method is to use an empirical correlation based on the Reynolds number. The empirical correlation requires the calculation of the Nusselt number which is defined as:

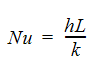
where h is the film coefficient, L is a characteristic length and k is the thermal conductivity. The Nusselt number is a ratio of convective to conductive heat transfer. The correlation that is used by Autodesk Simulation CFD to calculate the Nusselt number is:

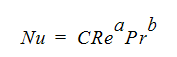
where Pr is the Prandtl number, a, b and C are constants. Note that both the Nusselt number and Reynolds number are dependent on a length. These lengths are not necessarily the same and frequently are different. The Reynolds number length is usually an opening length, a cylinder diameter or step height. The Nusselt number length is generally the length along the surface for which film coefficients are being calculated.

Bulk and Average Quantities

There are two methods that can be used to represent average values of the dependent variables. The first method that can be used is the bulk value, which is a mass-weighted average calculated using:

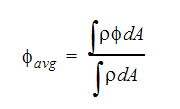
In this equation, we are calculating the bulk 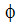at some location in the solution domain. The integral in this equation is taken over all of the element faces at this location.

Another method for calculating average quantities is to use the arithmetic mean value calculated as:

From these two equations, you can see that the mass-weighted average may not correspond to the arithmetic average value. For example, the arithmetic average velocity will be the same as if calculated by:

However, the bulk velocity may not satisfy this equation.

Distributed Resistances

For geometries with numerous flow obstacles, distributed resistances can be used to reduce the overall size (number of finite elements) of the problem. Rather than model each flow obstacle with the detail required to resolve pressure and velocity gradients, the flow obstacles can be modelled on a much larger scale and represented by a sink term in the momentum equations. They are effectively modelled as an extra pressure drop. In a shell-and-tube heat exchanger for example, the tubed region can be modelled using a distributed resistance term rather than modelling each tube individually. This modelling technique can be used to model vents, louvres, packed beds, gratings, tube banks, card cages, filters and other porous media.

There are three forms which the distributed resistance terms can take. The first is the loss coefficient form, where the excess pressure gradient is written as:

where the i indicates a global coordinate direction. The K-factor can be determined from measurements of pressure drop versus flow rate. This factor can also be found in fluid resistance handbooks such as: Handbook of Hydraulic Resistance, 3rd edition by I.E. Idelchik, published by CRC Press, 1994 (ISBN 0-8493-9908-4). Note that the K-factor used by Autodesk Simulation CFD has units of length-1. Most handbooks use an unit-less K-factor.

The second form for entering distributed resistances is the friction factor method. In this form, the excess pressure gradient is written as:

where f is the friction factor and D_H is the hydraulic diameter. The friction factor can be calculated using the Moody relation:

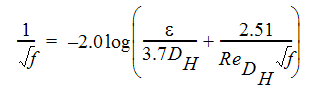
where 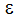is the surface roughness in length units and DH_H is the hydraulic diameter in length units.

Friction factor can also be calculated using the relation:

where a and b are constants.

The last form for the distributed resistance terms follows the Darcy relation:

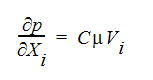
where C is called the viscosity coefficient and is the inverse of the permeability and is the fluid viscosity.

The form which should be used depends upon the information that is available. As mentioned previously, if pressure drop versus flow rate data is available, the K-factor method is probably the best. For some packed beds, the permeability may be available and the last form is best. For geometries with large banks of tubes, the friction factor may be the most suitable form.