Working with Fluid Materials

To Assign a Fluid Material

  1. Open the Material quick edit dialog. There are several methods:
    • Left click on the part, and click the Edit icon on the context toolbar.
    • Right click on the part, and click Edit...
    • Right click on the part name under the Materials branch of the Design Study bar, and click Edit....
    • Click Edit in the Materials context panel.
  2. Select one or more parts.
  3. Select the database from the Material DB Name menu.
  4. Select Fluid from the Type menu.
  5. Select the material from the Name menu.
  6. Click Apply.
Note: Care should be taken to avoid placing two different fluids in direct contact. Different fluids can exist in the same analysis if they are separated by a solid.

Example of Fluid Material Assignment

To Create a Fluid Material

Use the Material Editor to define fluid materials.

  1. To open the Material Editor, click Material Editor on the Materials context panel.
  2. Click the List button.
  3. Right click on a custom database, and select New material. Select Fluid. Specify a Name.
  4. Click the property button that is to be defined.
  5. For each property: Select the Variation method, enter the appropriate value and units, and click Apply.
  6. Optionally, click Save.
  7. Click OK. The new material is available when the Materials quick edit dialog is opened.

The Default material database contains at least one instance of every material type. A convenient way to create a new material is to use a Default material as an example. Because these materials are read-only, use the Material Editor to copy the original into a custom database, and modify the copy. For more about creating a material from an existing material...

Fluid Properties

There are six basic properties that are needed to define a fluid. Most of these properties can be made to vary with temperature, pressure or scalar, in several different ways. The following table lists the properties and the available variation methods.

Property Variational Methods
Density: the amount of mass per volume Constant, Equation of State, Polynomial, Inverse Polynomial, Arrhenius, Steam Table, Piecewise Linear, and Moist Gas
Viscosity: dynamic (absolute) viscosity is used Constant, Sutherland, Power Law, Polynomial, Inverse Polynomial, Non-Newtonian Power Law, Hershel-Buckley, Carreau, Arrhenius, Piecewise Linear, and Steam Table, First Order Polynomial, Second Order Polynomial
Conductivity: the thermal conductivity Constant, Sutherland, Power Law, Polynomial, Inverse Polynomial, Arrhenius, Steam Table, Piecewise Linear
Specific Heat Constant, Polynomial, Inverse Polynomial, Arrhenius, Steam Table, Piecewise Linear
Compressibility

Choice of:

Cp/Cv (gamma, the ratio of specific heats) -- useful only for compressible gas analyses or

Bulk Modulus -- useful only for compressible liquid analyses. See note below about Bulk Modulus.

Emissivity -- useful for radiation analyses. The emissivity specified on a fluid is assigned to contacting walls. Note that the emissivity assigned to a solid will override the value assigned to a contacting fluid.

Constant, Piece-wise Linear variation with temperature. (This is useful for spectral radiation analyses.)

Wall Roughness -- useful for applying variable roughness height to include effects of friction

Constant.

See note below about the Wall Roughness property.

Phase

Use for cavitation.

Specify the vapor pressure or a related material that contains the vapor properties.

Bulk Modulus

The bulk modulus and the density of a liquid are key to determining the speed of sound through that liquid:

The definition of bulk modulus is:

Given that the speed of sound, a, is defined as:

This works out to be: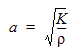

Source: White, F. M., “Fluid Mechanics,” McGraw Hill, New York, New York, 1986.

The bulk modulus is used only for compressible liquid (water hammer) analyses. The value of bulk modulus is automatically set for the liquid materials included in the Material Data Base. For user-defined materials, the correct value of bulk modulus is only required if liquid compressibility is to be analyzed. An example of a liquid compressibility, water hammer, is described:

Water is flowing through a straight pipe at 10 in/s. At a certain time, a valve at the end of the pipe is suddenly closed. A pressure pulse will move through the water at the speed of sound through water. This phenomena is called a “water hammer”, and is analyzed with a transient analysis to predict the movement of the pressure wave through the water. Instead of using the Ideal Gas Law and the ratio of specific heats to determine the sound speed, we will use the density and the bulk modulus of the water.

Wall Roughness

Enter a physical dimension (in the units available in the drop menu) of the roughness height. Such heights are typically very small--cast iron pipes, for example, have a typical wall roughness height of 0.0102 inches.

A value of wall roughness height specified on a fluid is automatically applied by the Solver to the wetted walls touching that fluid. A value of wall roughness height specified on a solid is applied to all wetted surfaces (surfaces contacting a fluid) of the part. A non-zero wall roughness height applied to a solid will prevail over a wall roughness applied to a fluid that touches it.

Wall roughness heights are implemented into the turbulence wall model, and do not affect the geometry. The flow must be turbulent for wall roughness heights to take effect. They will be ignored for laminar flows.

Specified wall roughness heights work best when closely adhered to the Turbulent Law of the Wall. This means that the non-dimensional distance (y+) from the wall node to its near-wall node must be between 35 and 350. The easiest way to enforce this constraint is by checking the Automatic Layer Adaptation box on the Mesh Enhancement dialog (found on the Meshing task). This will allow the Solver to adjust this near wall node distance along all walls in the model, based on the local flow conditions.

Real Gas Effects

To simulate real gas effects while still using the Ideal Gas Law, modify the gas constant on the material property window according to the consistency of the real gas. For a multi-species gas, the calculate the density using:

where P is the absolute static pressure, Ru is the Universal Gas Constant,T is the absolute static temperature, MWi is the molecular weight of species i and f i is the mole fraction of species i.

To incorporate this gas into Autodesk Simulation CFD, modify the Gas Constant on the Fluid material editor according to:

where RT is the value that you would enter on the Autodesk Simulation CFD window for the Gas Constant.

Parent topic: Materials and Devices