Several of the turbulence models used by Autodesk Simulation CFD use a two-equation model to determine the eddy viscosity and eddy conductivity variables. The two equations describe the transport of the turbulent kinetic energy, K and the turbulent energy dissipation, . The eddy viscosity and eddy conductivity are calculated using:
where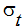 
is a turbulent Prandt number, usually taken to be 1.0 and 
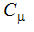is an empirical constant. The transport equations for K and 
are derived using moments of the momentum equations. For the default high Reynolds number k-epsilon turbulence model, they are:
Turbulent Kinetic Energy (TKE) Equation:
Turbulent Energy Dissipation (TED) Equation:
where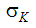 
and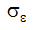 
are turbulent Schmidt numbers, C1 and C2 are empirical constants. All of the modelled constants associated with this model are listed in the following table. With these two equations, there are now 9 equations in 9 unknowns: 
.
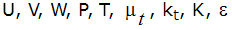| Constant | Value | Autodesk Simulation CFD Name | Result of Increasing Value |
|
|
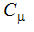
0.09 | CMu | more mixing, mores shear, greater change in pressure |
| C1 | 1.44 | CE1 | less mixing, lower shear, smaller change in pressure |
| C2 | 1.92 | CE2 | more mixing, mores shear, greater change in pressure |
|
|
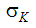
1.0 | (not available for user modification) | |
|
|
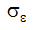
1.3 | (not available for user modification) |
The two-equation turbulence model just described has been used for numerous applications and generally works quite well for most engineering applications. However, this turbulence model does not predict separation points as accurately as is sometimes required. To improve the prediction of separation without greatly increasing the complexity of the analysis and usually the ability to obtain a solution, another two-equation model called the RNG two-equation model is also available in Autodesk Simulation CFD. In this model, the momentum equations are transformed to wave-number space and re-normalization group theory is used to derive the equations for calculating eddy viscosity. Because the resulting equations have a firmer theoretical foundation, the results using the RNG model are usually more accurate. However, this model is less stable numerically and hence subject to more convergence difficulties. It is probably best to start an analysis with the original two-equation model and then switch at some point to the RNG model.
The RNG turbulence model is also an eddy viscosity turbulence model. The turbulent kinetic energy and turbulent dissipation rate are calculated as before. The difference between the two turbulence models lies in the determination of the constants in Table 2. The values for the RNG model are listed in Table 3 with C1 calculated using the expression:
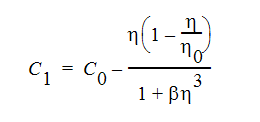
where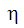 
is defined as:
| Constant | Value | Autodesk Simulation CFD Name | Result of Increasing Value |
|
|
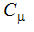
0.085 | CMu | more mixing, mores shear, greater change in pressure |
| C0 | 1.42 | RNG CE0 | less mixing, lower shear, smaller change in pressure |
| C2 | 1.68 | CE2 | more mixing, mores shear, greater change in pressure |
|
0.015 | RNG Beta | more mixing, mores shear, greater change in pressure |
|
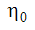
4.38 | RNG Eta | more mixing, mores shear, greater change in pressure |
|
|
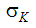
0.7179 | (not available for user modification) | |
|
|
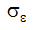
0.7179 | (not available for user modification) |
The two turbulence models described above are appropriate for high Reynolds number flows or flows where the dominant flow regime is fully turbulent. However, for flows where there are large regions of the problem domain that are laminar or in cases where the flow may start out turbulent, but may end in a laminar flow regime or vice versa, the above models may suffer in accuracy. This does not include the laminar regions in the boundary layers, but is more common in problems with large stagnant open spaces or problems with lots of obstructions that may block the flow and reduce the local flow velocities. In these cases, a low Reynolds number turbulence model is more appropriate. The model that is used in Autodesk Simulation CFD is again a two equation model that is solved for turbulent kinetic energy, K and the turbulent energy dissipation, . The equation used for K is:
Turbulent Kinetic Energy Equation:
The equation for is:
Turbulent Energy Dissipation Equation:
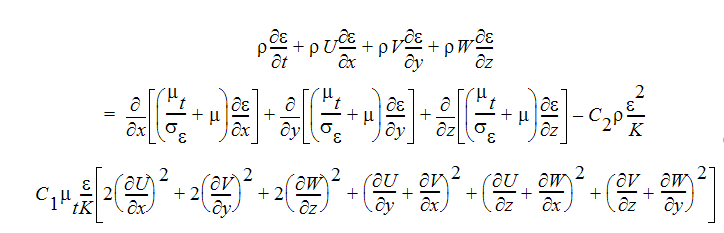
The constants in these 2 equations are the same as in the table above except for these 2 constants:
where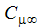 
is the same as the value for the high Reynolds model and Rt is the turbulence Reynolds number:
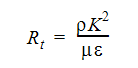
The other constant that varies is:
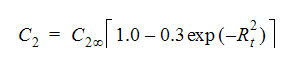
where 
is the same as the value for the high Reynolds model and Rt is again the turbulence Reynolds number.
Inflow Boundary Condition
Inlet boundary conditions must be specified for K and . In rare cases, these values are available. However, in most practical applications, they are not and estimates must be made for them. In order to arrive at these estimates, some definitions will be needed.
The turbulent kinetic energy is defined as:
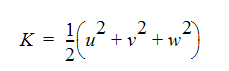
where the velocities in this equation are the fluctuating portion of the velocity. The turbulence intensity is defined as:
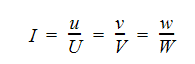
The combination of two equations above yield an estimate for the inlet turbulent kinetic energy based on the inlet velocity distribution:
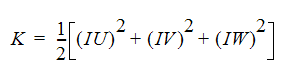
The turbulence intensity is more frequently available or can be more easily guessed. This value can be entered using theTurbulence button on the Analysis dialog. It is listed as the Turbulence Intensity. A default of 5% is used for internal flows and 1% for external flows. If the incoming flow is highly turbulent such as in swirling flows, a higher value on the order of 10-20% may be substituted for the default. In many internal flow cases, the inlet values do not play a significant role in the downstream effects where local shear dominates the turbulence quantities.
The turbulent energy dissipation can be defined in terms of length scale as:
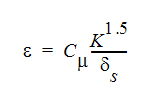
where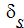 
is the length scale. The length scale is calculated automatically by Autodesk Simulation CFD. A different scale is used depending on whether the flow is internal or external. Autodesk Simulation CFD will also automatically determine whether the flow is internal (lots of walls) or external (few walls).
Wall Model
Both of the high Reynolds number turbulence models discussed in the previous section are only strictly applicable in the fully turbulent regime and do not apply to the inner layers of the boundary layer. The “low Reynolds number” model discussed above applies all the way to the no-slip wall. Hence, this model can be used in the boundary layer and also theoretically applies to re- laminarization zones as well. The low Reynolds number model does require that several nodes (3-10) be placed within the boundary layer (y+ values of 1 to 5). With mesh enhancement, this criterion is most likely satisfied. The boundary conditions for K and at the walls are applied automatically by Autodesk Simulation CFD.
For the high Reynolds number turbulence models, we use wall functions to model the turbulent flow next to the wall. The “wall functions” replace the turbulence model in the wall elements and generally only require the placement of one node in the boundary layer. The use of wall functions with high Reynolds number turbulence models do quite well for most turbulent flows.
The main purpose of the wall functions is to enforce the Law of the Wall, which can be written as:
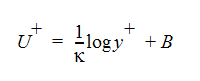
where B and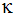 
are dimensionless constants. The inner variables U+ and y+ are defined as:
where Ut is the velocity tangent to the wall,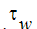 
is the wall shear stress, 
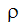is the density, 
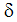is the distance from the wall, and 
is the kinematic viscosity. Autodesk Simulation CFD adjusts the wall effective viscosity based on the velocity and fluid properties next to the wall to enforce the Law of the Wall. With the exception of separating flow, the Law of the Wall is quite valid in the range:
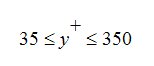
The y+ values calculated by Autodesk Simulation CFD are output to the post-processor files so they can be plotted. For some of the verification problems which were done by Autodesk Simulation CFD, we found that y+ values below 35 were usually associated with under-predicting the pressure drop in internal flows. Values of y+ above 350 corresponded to over-predicting the pressure drop in internal flows. Also, it is not uncommon to observe y+ values outside of this range near the inlet, especially if a uniform velocity field is specified at this boundary.
For rough walls, the Law of the Wall is modified as:
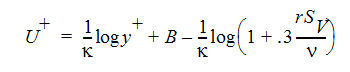
where r is the average roughness height (in length units) measured from the wall, is the kinematic viscosity and Sv is the shear velocity. The default value of r is 0.0, so the extra roughness terms disappear as a result. This roughness value is assigned in the Material Property windows. The values assigned to the solid materials will over-ride the value from the adjacent fluid material.
The wall constants and their default values are listed in the following table.
| Constant | Value | Autodesk Simulation CFD Name | Result of Increasing Value |
| A+ | 26.0 | VanDriest | less thermal mixing in wall boundary layer |
| B | 5.50 | Wall Parameter | lower wall shear, smaller change in pressure |
| r | 0.0 | Roughness | higher wall shear, greater change in pressure |
|
|
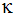
0.40 | Kappa | higher wall shear, greater change in pressure |
For turbulent heat transfer problems, the Temperature Law of the Wall is enforced. Two different forms of this relationship are used by Autodesk Simulation CFD depending upon the relative values of the turbulent and laminar Prandtl numbers. The difference between the two equations is which expression is substituted for the eddy viscosity distribution near the wall. In the first case, Spalding’s Inner Law [1] is used to obtain:
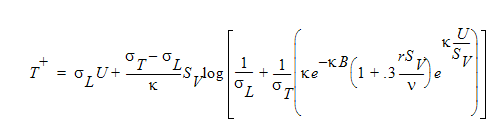
where is the laminar Prandtl number and is the turbulent Prandtl number. The laminar Prandtl number is:
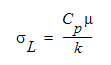
Here, Cp is the specific heat, is the absolute viscosity and k is the thermal conductivity. T+ is defined as:
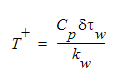
where 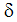is the distance from the wall, 
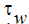is the wall shear stress and kw is the thermal conductivity in the wall layer. This formula for the Temperature Law of the Wall is used for laminar Prandtl numbers which are less than the turbulent Prandtl number, which is assigned the value of 1.0 by Autodesk Simulation CFD. So, most air or gas flows should use this formula.
For fluids with higher laminar Prandtl numbers (like water), the Van Driest formula for eddy viscosity is used in the Temperature Law of the Wall to yield:
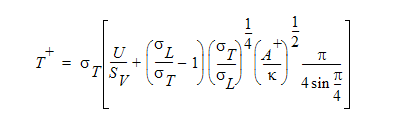
where A+ is Van Driest’s constant. This constant is assigned the value of 26.0 by Autodesk Simulation CFD. It can be modified by clicking theTurbulence button on the Analyze task, and clicking the Advanced button on the Turbulence dialog.