For the case where Ohmic or Joule heating is to be considered, the following energy equation applies for incompressible flow:
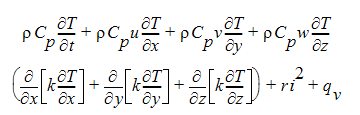
where i is the magnitude of the current density and r is the electical resistivity, a material property. With this equation, an equation to determine the electric current in the Ohmic term ri2 must also be solved. We use the electric potential equation:
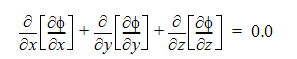
where is the electric potential and the current is found using:
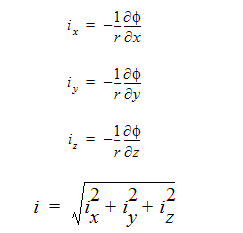
The variables used in these equations are defined in the table below:
| Variable | Description (sample units - SI system) |
| Cp | constant pressure specific heat (J/kg-K) |
| i | electric current density (amps/m2) |
| k | thermal conductivity (W/m-K) |
| qv | volumetric heat source (W/m3) |
| r | electrical resistivity (Ohm-m) |
| T | temperature (K) |
| t | time (s) |
| u | velocity component in x-direction (m/s) |
| v | velocity component in y-direction (m/s) |
| w | velocity component in z-direction (m/s) |
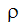
|
density (kg/m3) |
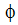
|
electric potential (Volts) |
The boundary conditions for the energy equation include the usual specified temperature, film coefficient, heat flux or radiation to an external source. The boundary conditions on the electric potential equation include a specified voltage or a specified electric current.