The techniques and associated nomenclature used during the solution of the coupled equations are defined in this topic.
The sequence of operations in the Autodesk Simulation CFD segregated solver are shown:
- Read in geometry, boundary conditions, and analysis data
- Create data structures
- Solve x-momentum equation
- Solve y-momentum equation
- Solve z-momentum equation
- Solve pressure equation and correct velocities
- Solve energy equation
- Solve turbulent kinetic energy equation
- Solve turbulent energy dissipation equation
- Check convergence (go to step 3)
- Perform output calculations
- Write out data
- Exit
Note that each of governing equations are solved separately. Also, if the analysis is isothermal, the energy equation solution is skipped. Likewise if the analysis is laminar, the turbulence equations are skipped.
Another item that you may notice is that the solver arrow sometimes spends almost no time on the V velocity and W velocity equations. Because of the similarity of the momentum equations, we can sometimes set up only the U velocity and use that setup for the other two momentum equations.
Global Iterations
Because the governing equations are non-linear, they must be solved iteratively. A Picard or successive substitution method is used. In this method, estimates of the solution variables (U, V, W, P, T, K,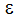 
) are substituted into the governing equations. The equations are solved for new values which are then used as the estimates for the next pass. The global iteration is shown in Figure 1 inside the dashed line box. Autodesk Simulation CFD will either perform a fixed number of these global iterations, or it will check for the convergence criterion, or it will stop when either is reached. The convergence criterion is the level at which the specified variable’s residual norm must reach. The residual norm is defined in the next sub-section. In conjunction with the comments made earlier, we recommend that the pressure equation be the one on which solution convergence is measured.
Convergence, Residuals, and Residual Norm
Hopefully, as we march through the global iterations just described, the values that are calculated at each step are getting closer and closer or converging to the correct solution. Since the correct solution is not known apriori, some measure of the convergence must be found. There are any number of parameters which can be used to check the level of solution convergence. Many have been tried. No one value is best for every situation. However, we have found that the parameter which yields the most information for the widest range of problems is the residual norm.
First, the residual must be defined. After the governing equations have been discretized, they will become a set of algebraic equations for the dependent variables: U, V, W, P, T, K, 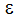. For each of these variables, there will be an equation for each finite element node in the analysis model. A typical algebraic equation for variable 
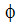at node i can be written as:
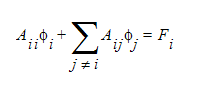
where Aij are the algebraic coefficients resulting from discretizing the advection and diffusion terms in the governing equation and Fi are the discretized source terms. The residual of this equation is defined as:
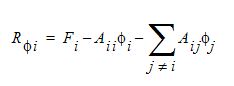
where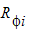 
is the nodal residual for at node i.
With each pass through the segregated solver or global iteration, these residuals should become smaller if the solution is converging. Rather than plotting each nodal residual after every global iteration, the norm of the nodal residuals is calculated. The norm effectively combines all of the nodal residuals into a single number:
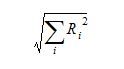
As with the nodal residuals, the norm of the residuals should also get smaller as the solution converges. The norm of the nodal residual is what Autodesk Simulation CFD prints in the status file to indicate convergence.
Other indicators of convergence include looking at the minimum, maximum and average values of the dependent variables. All of these parameters should asymptote to a single value. When this happens, the solver is no longer significantly changing these values and the solution can be considered converged. The ultimate test of convergence is to look at the results of the analysis in the post-processor at different global iterations. If the results do not change appreciably between the two runs, the solution may be converged enough for your purpose.