The calculation of these stresses involves several steps. We begin by integrating the six stresses, σ N , σ T , σ H , τ NT , τ TH , τ NH , along SCL to obtain the total load (F N , F T , F H , F NT , F TH , F HN ) using:
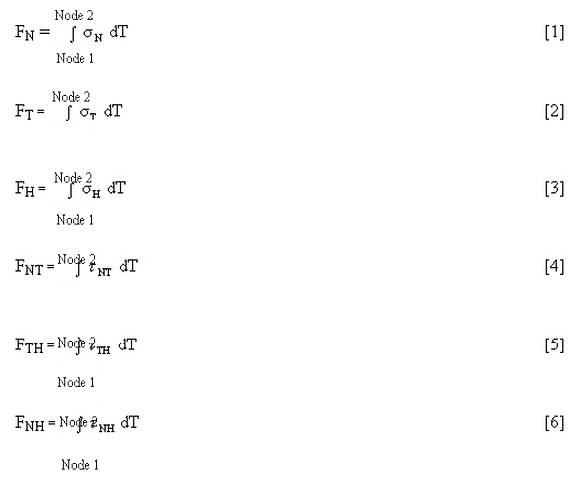
Where T is the location along the SCL.
Then, we calculate the membrane stress (F/A) for all 6 components. For an SCL of length t,
The principal membrane stresses (
) are obtained from the tensor whose components are given by equations 7 through 12. These stresses are obtained by recasting this tensor in principal axis.
Next we develop the bending stresses by subtracting the membrane stress from the total stress distribution. This is done stress point by stress point. We only need to consider the two component stresses perpendicular to the SCL (nominally the hoop and meridional component stresses). First, we develop the moment-load distribution for an SCL of length t. Then we integrate the moment load-distribution to obtain the moment on the cross section.
Again, these integrals should be calculated using trapezoidal integration. The subsequent results are used to calculate the bending stress (Mc/I) for an SCL of length t from:
The next step is to calculate the principal stress at each end of the SCL (
). These principal membranes plus bending stresses are obtained from the tensor whose components are obtained by substituting T = Node 1 and T=Node 2
The membrane stresses are obtained from equations 7 through 12, and the bending stress from equations 16 through 18. Again, note how one gets two sets of principal stresses: one at T=Node 1 and another at T=Node 2. Again, the principal stresses are obtained by recasting the tensor in principal axis.
At this point we have all the principal stresses,
and
,
required to determine the two output scalar quantities: P m and P m + P b :
|
P m = Largest of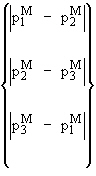 
|
(25) |
|
Pm + Pb = Largest of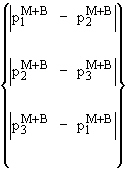 
|
(26) |
Note how equation 26 must be evaluated twice because there exist two sets of values: one at T=Node 1 and another at T=Node 2. The output quantity should be that of the evaluation that resulted in the largest value.
Reference: ASME SGDA-99-2, PROPOSED NON-MANDATORY APPENDIX for Subcommittees III & VIII, Interpretation of Finite Element Analysis Stress Results, Rev 4, 2000.