Activating the command: Setup Model Setup
Model Setup Parameters
Parameters Advanced
Advanced Equilibrium and Time-Step tabs
Equilibrium and Time-Step tabs
The information on this page applies to the following analysis types except if indicated:
Mechanical Event Simulation (MES)
Static Stress with Nonlinear Material Models
MES Riks Analysis
Convergence Criteria
During each time step of an analysis, the processor will perform iterations to converge on a solution. After the number of iterations specified in the Maximum number of iterations field in the Equilibrium tab is reached, the time step will be cut in half and the iterative process will begin again. If the Automatic check box is activated, the processor will set the number of iterations based on the other settings in the model. (15 iterations if the model has no contact, 30 iterations if it has contact.)
The convergence of the solution can be based on two results, displacement and energy. Energy is a product of the displacement and force tolerances. This must be selected in the Convergence criteria drop-down box. The convergence will be compared to the values specified in the Displacement tolerance and Force tolerance fields. (See Figure 1.) The displacement tolerance can either be entered by the user or set by the processor based on other settings in the model when Automatic check box is activated. (0.005 with contact and 0.0001 without contact.)
|
|
| Figure 1: Convergence Tolerance |
|
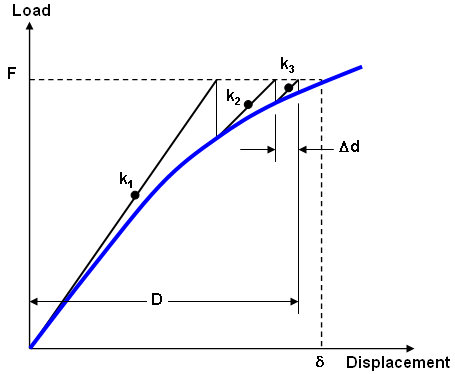
The blue curve shows the theoretical stiffness (Load/Displacement) of a model. The displacement δ for an input force F is appropriate. In a nonlinear analysis, a number of iterations calculate the stiffness along the curve (k 1 , k2, k 3 ,). The solution is considered to be converged when the displacement in the last iteration (Δd) compared to the overall displacement D is less than the convergence tolerance (Δd/D < tolerance). |
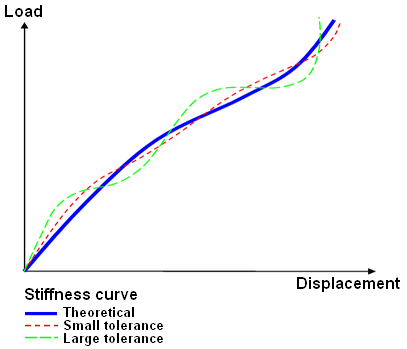
Analyses with large dynamic effects need a smaller tolerance. (Highly dynamic analyses may also require time steps small enough to capture the wave propagation through an element, proportional to the square root of stiffness/mass.) Analyses with simple loading can use a larger tolerance if 10% to 20% accuracy is sufficient. See Figure 2. As with all FEA, multiple runs with different tolerances may be required to determine the effect of the tolerance size.
|
| Figure 2: Schematic of Effect of Tolerance Size on Solution |
If the convergence is based on displacement, there are three methods that can be used for the convergence. These are selected in the Convergence based on drop-down box. If the Total displacement option is selected, the results from the beginning of the analysis will be used for convergence. If the analysis involves large scale motion, this method will result in a relatively loose tolerance criterion. The displacement tolerance should be set low (1e-6 to 1e-15) when using this convergence method. If the Displacement from last time step option is selected, the results from the last time step will be used for convergence. This method is very accurate for analyses with relatively small time steps. This method is the default and is useful for analyses that involve large scale motion. The displacement tolerance can be set around 1e-3 to 1e-5 for this method. If the Displacement from first iteration option is selected, the results from the first iteration of the current time step will be used for convergence. This is more conservative than the Displacement from last time step method but requires at least two iterations at each step which will increase the analysis run time.
Convergence Tolerance Relaxation
If the analysis is reducing the time step significantly (L column in the log file increasing), the analysis is having difficulty converging. If the convergence difficulty is a temporary effect, it may be acceptable to use a larger convergence tolerance to let the model to converge and then continue with the next time step.(Otherwise, the analysis may continue to reduce the time step and possibly reach the point where the analysis fails to converge entirely.) Such behavior can be obtained with the Activate convergence tolerance relaxation control on the Time-Step tab.
When Activate convergence tolerance relaxation is activated, the convergence tolerance (the Displacement tolerance or Force tolerance entered on the Equilibrium tab) will be multiplied by the Relaxation factor input each time the automatic time step level (L column in the log file) is reduced by the multiple entered in the AutoTM level field. For example, with this input
|
Displacement tolerance |
= 1E-4 |
|
AutoTM level |
= 6 |
|
Relaxation factor |
= 5 |
the following convergence tolerance would be used during the analysis if the time step level reached the indicated value:
| AutoTM Level (L) | Convergence Tolerance |
|
1 through 6 |
1E-4 |
|
7 through 12 |
(1E-4)*5 = 5E-4 |
|
13 through 18 |
(5E-4)*5 = 2.5E-3 |
|
19 |
(2.5E-3)*5 = 1.25E-2 |
|
20 |
Reached autotm limit. The analysis stops. |
See also Setting Up and Performing the Analysis: Performing the Analysis: Performing A Nonlinear Analysis for information on the log file and convergence while the analysis is running.
- Increasing the convergence tolerance may have an effect on the accuracy of the results. When used improperly, the results could be inaccurate or incorrect. The Activate convergence tolerance relaxation option is not recommended for history- or path-dependent analyses.
- For example, an impact analysis with surface to surface contact will often reduce the time step to find the instant when the part transitions from no contact to full contact; the reduction is not necessarily due to a convergence problem. So to relax the convergence tolerance right when the maximum stress is likely to occur may have an undesirable affect on the results.
Stiffness Calculation
During the analysis the stiffness matrix can be reformed. You can control how often this occurs using the following input on the Equilibrium tab:
- Number of allowable stiffness reformation per time step: This input will only be used if a Combined Newton solution method is being used or if Use a constant time-step size is set on the Time-Step tab. It indicates how often the stiffness matrix is re-calculated for each time step. If the stiffness changes during each time step are small, then reforming the stiffness matrix at every iteration may add unnecessary calculation time to the analysis. In such situations, it may be faster to reformulate the stiffness matrix only a few times during the time step and let the processor perform more iterations (if necessary) to converge. When using the Modified Newton solution method, the processor ignores the input and uses a value of 1. When using the Full Newton solution method, the processor ignores the input and uses a value equal to the Maximum number of iterations.
- Matrix reform interval within each time step: This input will only be used if a Combined Newton solution method is used. It specifies how often the matrix is reformulated. A value of 1 will update the matrix on every iteration, a value of 2 will update the matrix every other iteration, and so on.
- Maximum stiffness reformations per interval: An interval is a set of equilibrium iterations.
- Number of time steps between reforming stiffness matrix:
- Number of time steps between iterations: This is the number of time-steps at which the processor iterates to converge to a solution. A value of 1 indicates that every time step must iterate to converge, a value of 2 indicates that every other time step will iterate to converge, and so on. Larger values result in a faster analysis because fewer time steps need to iterate to converge, but at the cost of potentially deviating from the solution at the time-steps that do not iterate. Tip: In some situations, the analysis has difficulty converging at time 0. Setting the Number of time steps between iterations to 2 will force the processor to skip the iterations on the first time-step and then iterate on the second time-step. This may avoid any instabilities at the beginning of the analysis and recover in the second time-step. Naturally, check the results to make sure skipping iterations has not caused the solution to converge to a wrong solution.