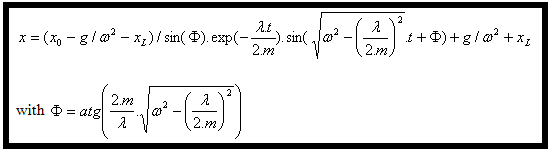Uno de los pasos responsables del proceso de diseño es la validación. Para validar un diseño, suele ser mejor utilizar casos teóricos fiables con los que establecer comparaciones. A continuación detallamos estos casos.
Los casos describen las ecuaciones y asunciones utilizadas para conseguir validar los resultados de una simulación.
Desplazamiento, caso del muelle-masa
Un caso sencillo de validación de muelle y masa.

Ley de Newton:
![]() (1)
(1)
Con:
| Valor numérico: | |
|---|---|
| |
|
| |
|
| |
|
| |
10 |
| |
20 |
| |
15000 |
| |
0.3 |
| |
9.81 |
| |
0.33 |
| |
0.0 |
|
(1) |
|
|
con |
|
|
|
|
|
Una solución para esta ecuación diferencial es: |
|
|
|
|
|
Una solución concreta, si el sistema está estabilizado, es para |
|
|
Seguidamente (2) |
|
|
|
|
|
|
|
|
Las condiciones iniciales proporcionan el valor de A y |
|
|
para t = 0.0, (3) |
|
|
|
|
|
y |
|
|
|
|
|
Por último, (4) y (6) se registran en (3) y se concluye la ecuación del desplazamiento: |
|
|
|
|
|
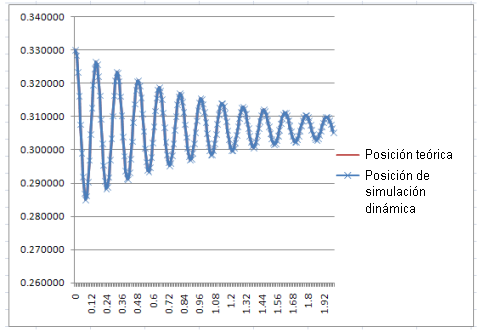
Esta ecuación se programa en Excel y los resultados se comparan con los producidos por Simulación dinámica. Son idénticos. |
|
 |
|
Posición y velocidad, caso del pistón-cigüeñal
La finalidad de este caso de validación es comprobar los datos de posición y velocidad de un mecanismo de cigüeñal y de pistón cuando se obtienen en Simulación dinámica, y comprobar que coinciden con los valores arrojados por las ecuaciones teóricas.
Valores conocidos: el “impulso” o la distancia del cojinete transversal del cigüeñal desde su centro de giro y la longitud de la varilla de conexión entre el cojinete transversal principal y la unión de pasador del pistón.
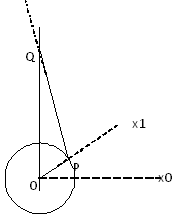
Diagrama
|
Definición |
R = longitud (OP) = impulso del cigüeñal L = longitud (PQ) = longitud de varilla de conexión |
 |
|
|
Velocidad del punto Q en relación al sistema de coordenadas absoluto R0 = (x0, y0) |
|
|
|
// posición de Q en R0 |
|
|
// velocidad de Q en R0 |
| con:
|
|
| y:
|
|
|
|
|
| con: |
|
| y; |
|
| Entonces: |
|
|
El punto Q permanece en el eje y0 y el componente x0 es 0.0 : |
|
|
|
|
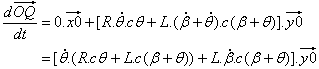 |
|
| Por último, utilizando (1): | |
|
|
|
|
La ecuación (1) proporciona |
|
|
(1) |
|
y 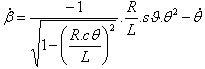 |
|
| Con MS Excel y valores numéricos (L=0.125 m, R=0.06 m y |
|
|
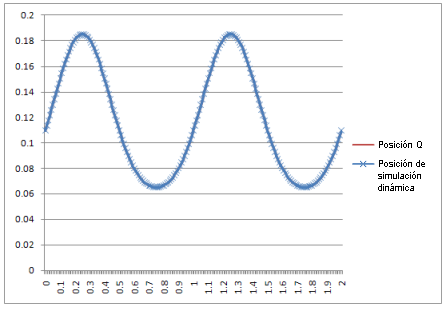
Posición: |
|
 |
|
|
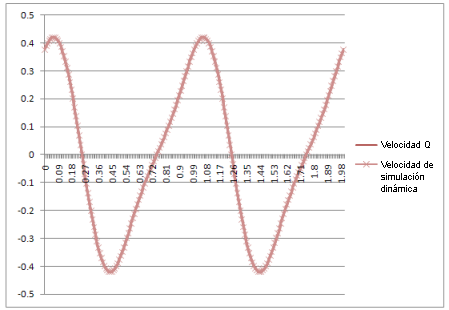
Velocidad: |
|
 |
|
El resultado: las curvas de la simulación dinámica son idénticas a las producidas por las ecuaciones teóricas.
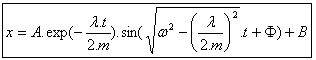 (3)
(3)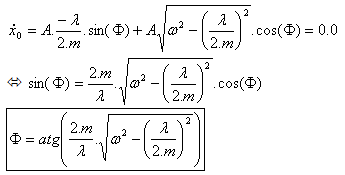 (5)
(5)