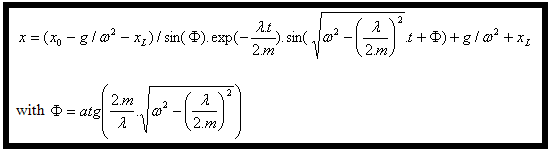L'une des étapes importantes de la conception est la validation. Pour valider une conception, il est souvent judicieux d'utiliser des cas théoriques simples et fiables comme outil de mesure. Vous trouverez ci-après quelques exemples de cas.
Ils décrivent les équations et hypothèses utilisées dans la validation d'une sortie de simulation.
Déplacement - Masse-ressort
Un cas de validation de masse et de ressort simple.

Loi de Newton :
![]() (1)
(1)
Avec :
| Valeur numérique : | |
|---|---|
| |
|
| |
|
| |
|
| |
10 |
| |
20 |
| |
15000 |
| |
0.3 |
| |
9.81 |
| |
0.33 |
| |
0.0 |
|
(1) |
|
|
avec |
|
|
|
|
|
Une solution pour cette équation différentielle est : |
|
|
|
|
|
Une solution particulière, lorsque le système est stabilisé, est pour |
|
|
Puis (2) |
|
|
|
|
|
|
|
|
Les conditions initiales donnent la valeur de A et |
|
|
pour t = 0.0, (3) |
|
|
|
|
|
et les |
|
|
|
|
|
Pour finir, (4) et (6) reportés en (3) donnent l'équation du déplacement : |
|
|
|
|
|
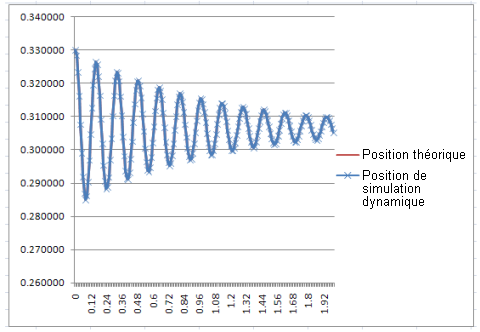
Cette équation a été ensuite programmée dans Excel et les résultats comparés avec ceux donnés par la simulation dynamique ; les résultats se sont avérés identiques. |
|
 |
|
Position et Vitesse - Vilebrequin et piston
L'objectif de cette validation est de vérifier la position et la vitesse d'un mécanisme de vilebrequin et de piston lorsque la sortie de la simulation dynamique et les équations théoriques aboutissent aux mêmes résultats.
Valeurs connues : la distance de la portée d'arbre depuis le centre de rotation du vilebrequin et la longueur de la tige entre la portée de roulement principale et la broche de liaison du piston.
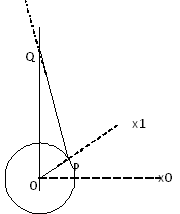
Diagramme
|
Définition |
R = longueur(OP) = portée d'arbre L = longueur(PQ) = longueur de la tige de connexion |
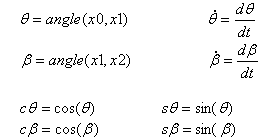 |
|
|
Vitesse du point Q relativement au système de coordonnées absolu R0 = (x0, y0) |
|
|
|
// position de Q dans R0 |
|
|
// vitesse de Q dans R0 |
| avec :
|
|
| et :
|
|
|
|
|
| avec : |
|
| et : |
|
| puis : |
|
|
Le point Q reste sur l'axe y0 et le composant x0 est 0,0 : |
|
|
|
|
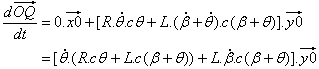 |
|
| Finalement, en utilisant (1) : | |
|
|
|
|
L'équation (1) donne |
|
|
(1) |
|
et  |
|
| En utilisant MS Excel et des valeurs numériques (L=0.125 m, R=0.06 m et |
|
|
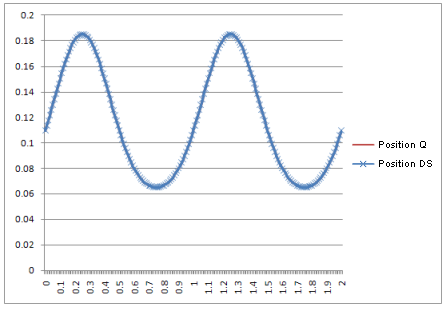
Position : |
|
 |
|
|
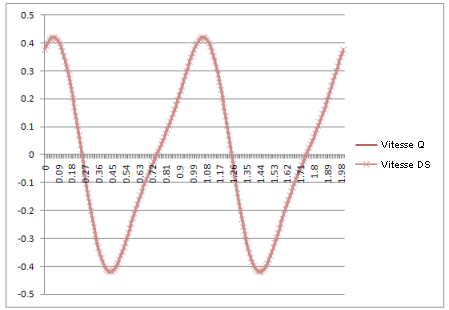
Vitesse : |
|
 |
|
Le résultat : les courbes de la simulation dynamique sont identiques à celles produites par les équations théoriques.
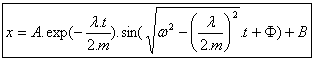 (3)
(3)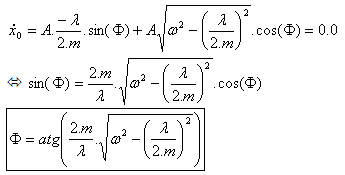 (5)
(5)