残留応力収縮予測モデルは、材料の温度 - 粘弾性の挙動が線形であることを前提として成り立っています。このモデルでは、金型の中で圧力を受けながら冷却されていく材料に発生する応力を考慮しています。この方法では、収縮歪を計算するのではなく、要素ごとに残留応力の分布を直接計算します。
残留応力分布によって、流動に対して平行および垂直な各要素の肉厚方向の応力が分かります。この応力分布を応力解析プログラムに入力すると、成形品の変形後形状が得られます。これに加え、材料の実験済みの収縮データがあれば、大幅に高精度な収縮予測ができ、その結果、残留歪方法を使用するよりも成形品の変形を正確に把握できます。
この方法の一般的な説明
このモデルは、材料の温度 - 粘弾性の挙動が線形であることを前提として成り立っています。このモデルでは、金型の中で圧力を受けながら冷却されていく材料に発生する応力を考慮しています。特に、材料の固化とそれに続く収縮の過程で温度変化によって発生する応力とともに、圧力によって引き起こされる応力にも注目したモデルです。圧力による応力は、固化層を形成する固体化した材料にかかる溶融樹脂の圧力の作用によって発生します。理論面に基づいていることから、このモデルには、材料の収縮データがなくても使用できるという利点があります。それでも収縮データを利用できれば、このモデルのパフォーマンスは大幅に向上します。
収縮と反りの予測は、熱と圧力によって発生する残留応力の分布を計算した結果に基づいています。現在の開発における計算手順を以下に示しています。これは繊維充填材料を対象としたものです。非充填材料でも計算手順は同様ですが、機械的特性の計算手順が不要になります。
各タイム ステップに対して
- 流体力学の計算
- 圧力 p、流量 Q...
- 繊維配向
- 熱伝達の計算
- 温度 T
- 固化層
- 熱力学の計算
- f (p, v, T)=0
- 粘度の更新
- 解析は収束するか。
- 収束しない場合、手順 1 から繰り返す。
- 収束する場合は、手順 6 に進む。
- マイクロメカニックスの計算
-
熱機械的特性:
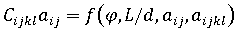
-
- 熱粘弾性の計算:
- 熱および圧力によって生じる応力:
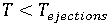 の場合、次のタイム ステップに進む(ステップ 1 から繰り返す)。
の場合、次のタイム ステップに進む(ステップ 1 から繰り返す)。
注: 残留熱応力の収縮モデルを選択すると、反り解析では非対称充填+保圧解析で得られた非対称情報が使用されます。非対称性は、金型の表面と裏面との温度差、または分岐の形状(またはその両方)が原因となって生じます。したがって、分岐形状を持つ成形品の場合は、冷却解析の結果がなくても、ある程度の非対称効果を反りの計算結果に見い出すことができます。しかし、充填+保圧解析が対称であれば、反り解析も対称となり、冷却差を無視できます。
収縮データがない場合のこの方法の適用
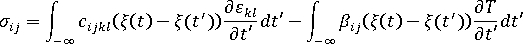
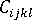 および
および 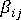 は、それぞれ材料の機械的特性および熱的特性を定義するテンソル
は、それぞれ材料の機械的特性および熱的特性を定義するテンソル 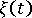 は材料の温度依存性を考慮した疑似時間スケールで、次のように定義する。 ここで
は材料の温度依存性を考慮した疑似時間スケールで、次のように定義する。 ここで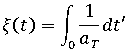
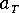 は時間-温度のシフト率で、材料および温度範囲に応じて WLF 方程式または Arrhenius 方程式によって決定する。
は時間-温度のシフト率で、材料および温度範囲に応じて WLF 方程式または Arrhenius 方程式によって決定する。
- 繊維強化材料ではない材料では等方性モデルを使用する。このモデルでは、機械的特性のテンソル
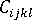 を、Autodesk Simulation Moldflow materialsデータベースに格納されている材料の係数とポアソン比で定義する。また、熱特性のテンソル
を、Autodesk Simulation Moldflow materialsデータベースに格納されている材料の係数とポアソン比で定義する。また、熱特性のテンソル 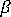 を定義するために使用する熱膨張係数は、 材料の pvT データから得られる。
を定義するために使用する熱膨張係数は、 材料の pvT データから得られる。 - 繊維充填材料の場合、これらのテンソルは複合材料の異方性の機械的特性と熱特性を使用して定義する。これらのプロパティは、充填+保圧解析で得られた繊維配向分布から算出する。このモデルでは、繊維配向に平行な方向と垂直な方向に発生する応力を予測する。
- 材料の温度がその転位温度を下回るまで、材料内部には応力が蓄積されません。
- x3 の方向が ローカルの中間面に垂直なローカル要素座標系では、せん断応力 =
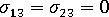 。
。 - 垂直応力
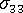 は 肉厚全体で一定である。
は 肉厚全体で一定である。 -
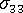 <0 であれば、材料は金型壁面に密着している。
<0 であれば、材料は金型壁面に密着している。 - 金型内に材料があれば、どの場合でも制限付きの急冷条件が規定される。
- 金型の弾性は無視する (金型コアの弾性は、コアシフト解析では考慮する)。
- 突き出された後の成形品の材料は、弾性固体としての挙動を示す。
このモデルは Autodesk Simulation Moldflow materialsデータベースのすべての材料で使用できます(収縮特性の有無にかかわらず)。繊維充填材料の場合、モデルは[プロセス設定ウィザード: 充填+保圧設定]ダイアログ ボックスで[繊維配向解析(繊維充填材の場合)]を実行するオプションを選択する必要があります。
このモデルを使用すると収縮の傾向を予測できますが、得られた絶対値に関しては、多くの誤差が存在することがあります。反りを低減するための設計では、このモデルは効果的ですが、収縮データが存在する場合に比べ、得られる絶対値の精度は低くなります。非充填材料の場合、流動解析ソフトウェアには分子配向や結晶化度の効果を計算する機能がないので、モデルは等方性です。
収縮データがある場合のこの方法の適用
- 収縮の転移温度と pvT データに対する高い依存性のため、現在の測定方法では、実際の成形条件下での挙動を表すことはできない。
- 分子配向を判断する手段がなく、したがって非充填材料の異方性をこのモデルでは予測できない。
- 結晶化度の効果に対して不十分である。
- 粘弾性の計算に使用する緩和スペクトルのデータがない。
Autodesk Simulation Moldflow で測定した収縮データが存在する材料であれば、測定収縮結果を考慮することで、その熱粘弾性モデルを大幅に改良できます。そのためには、測定で得られた収縮データに関連付けたハイブリッド モデルの独立変数の 1 つとして、理論モデルを使用します。これにより、収縮の実測値と予測値の差を小さくします。ここで得られたモデルを、補正済み残留金型内応力 (CRIMS: Corrected Residual In-Mold Stress) モデルといいます。
この考え方を次に示します。
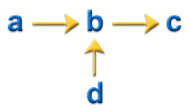
補正済み残留金型内応力 (CRIMS) モデル
. (a) 予測等方性残留応力 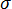 、(b) 誤差補正、(c) 補正済み異方性残留応力
、(b) 誤差補正、(c) 補正済み異方性残留応力 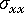 および
および  、(d) 実測の収縮
、(d) 実測の収縮
この効果の説明として、次のグラフを参照してください。
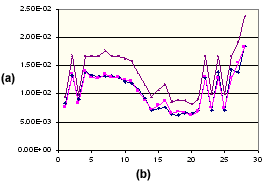
ポリプロピレンの平行収縮
. (a) 収縮 %、(b) 成形条件設定番号、![]() 平行方向実測値、
平行方向実測値、![]() 平行方向補正済み値、
平行方向補正済み値、![]() クリティカル計算値(等方性)
クリティカル計算値(等方性)
このグラフは、流動方向と平行な方向で測定した、ポリプロピレンの実験的な収縮を示したものです。同時に、熱粘弾性モデルを使用して計算した平行方向の理論的な収縮、およびそれを補正した値も示しています。補正済みの値が実測値ときわめて良好に整合していることは明らかです。同じポリプロピレンで流動方向に垂直な方向についても、次に示すように同様な改善効果が認められます。
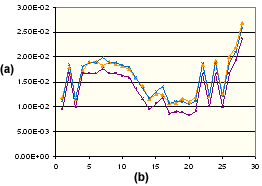
ポリプロピレンの垂直収縮
. (a) 収縮 %、(b) 成形条件設定番号、![]() 垂直方向実測値、
垂直方向実測値、![]() 垂直方向補正済み値、
垂直方向補正済み値、![]() クリティカル計算値(等方性)
クリティカル計算値(等方性)
この補正の概念は繊維充填材料にも適用可能で、同様に優れた結果を得ることができます。ガラス繊維強化で重量比 15% の PA66 で得られた結果を次に示します。
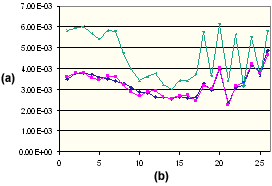
ガラス繊維強化 15% の PA66 の平行収縮
. (a) 収縮 %、(b) 成形条件設定番号、![]() 平行方向実測値、
平行方向実測値、![]() 平行方向補正済み値、
平行方向補正済み値、![]() 平行方向理論値
平行方向理論値
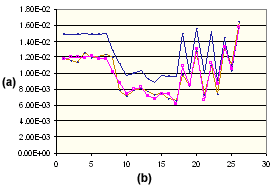
ガラス繊維強化 15% の PA66 の垂直収縮
. (a) 収縮 %、(b) 成形条件設定番号、![]() 垂直方向実測値、
垂直方向実測値、![]() 垂直方向理論値、
垂直方向理論値、![]() 垂直方向補正済み値
垂直方向補正済み値
単変量解析との併用によるこの方法の適用
単変量解析は、Autodesk Simulation Moldflow の反り解析に用意されている手法です。この解析は、反りの主要因を特定し、成形品の反りを低減する適切な手段を講じることを可能にします。詳細については、単変量解析のトピックで扱っています。ここでは、単変量解析の過程で残留応力法をどのように適用するかを見ていきます。
充填過程と保圧過程の充填+保圧解析では、次の情報が出力されます。これらの情報を、残留応力計算の入力として使用できます。
- ローカル要素軸系での各要素の一般化した力、つまり、膜力(
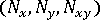 )および曲げモーメント(
)および曲げモーメント(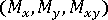 )
) - 各要素の材料配向の角度
- 各要素の機械的特性(縦ヤング率、横ヤング率、およびポアソン比)
単変量解析は、反りの原因を次の 3 つに分類する考え方に基づいています。
- 冷却差
- 収縮差
- 配向の影響
この考え方は、応力よりも、むしろ収縮に関連したものです。したがって、残留応力モデルを使用する場合に、上記の 3 種類の効果の観点から反りの原因を特定するには、まず与えられた一般化した力から、一般化した歪を算出する必要があります。次に、この歪を冷却差、収縮差、および配向の影響に起因する成分に分解します。最後に、その修正した歪を、元の対応する一般化した力に変換し直します。それぞれの効果について個別に応力解析を行い、反りの計算結果を求めます。この計算に関連する数式を以下にまとめます。
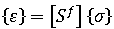
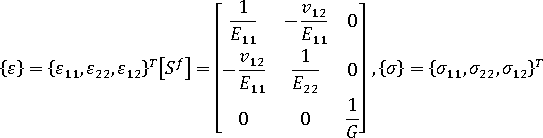
また、次のように剛性マトリックスの観点からフックの法則を記述することもできます。
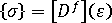
ここで、
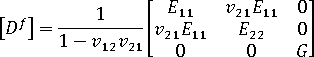
材料配向の角度 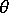 を与えることで、コンプライアンス マトリックスと剛性マトリックスを配向系からローカル要素系に変換します。
を与えることで、コンプライアンス マトリックスと剛性マトリックスを配向系からローカル要素系に変換します。
一般化した歪は次の式で得られます。
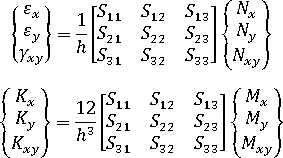
ここで、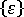 および
および 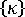 はそれぞれ歪ベクトルと曲率ベクトルです。
はそれぞれ歪ベクトルと曲率ベクトルです。
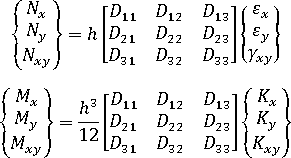
反りの効果を分離するには、 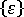 、および
、および 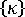 を分解した成分で置き換えた後、膜力と曲げモーメントを再計算し、得られた新しい値を構造解析で使用します。
を分解した成分で置き換えた後、膜力と曲げモーメントを再計算し、得られた新しい値を構造解析で使用します。