射出成形では、金型の中に成形品が拘束されています。射出成形品が固化する間、固化層の収縮は 2 つのメカニズムで抑制されます。成形品が突き出されて金型から分離すると、これらの残留応力は収縮変形の形で解放されます。
金型内にある間、固化層の収縮は 2 つのメカニズムで抑制されます。まず、金型壁面に成形品が吸着することで、固化層の少なくとも表層の移動を抑制します。次に、新しく形成された固体表面が、溶融樹脂の圧力による伸張力で固定されたまま維持されます。
固化の段階では、キャビティの内部に残留応力が蓄積されていきます。急速な冷却が抑制されていることから、残留応力の分布は、固化層比率と結び付けて考えた圧力変化の履歴によって大きく決まります。いったん成形品が突き出されて金型から外れると、これらの残留応力は収縮変形の形で解放されます。キャビティ内の残留応力と等価な初期歪が成形品内部で均一に分布して入れば、成形品は反りや成形後の残留応力を発生せずに、均一に収縮します。成形品各部で収縮に差があると、反りが発生します。
収縮差には次の 2 種類が考えられます。
- 領域ごとの収縮差 (収縮差)
- 通常の薄肉成形品では、この形態の収縮差は 2 種類に分類できます。1 つは主に冷却差に起因する肉厚方向の差で、もう 1 つは表面の領域ごとの差です。
- 方向ごとの収縮差 (配向の影響)
- 繊維充填熱可塑性材料では、平行方向と垂直方向との収縮差、および繊維配向の分布に関連する材料特性の異方性が、成形品に発生する反りの要因の 1 つとなります。
射出成形品の収縮は、成形中の材料に見られる熱力学的挙動で左右されます。わかりやすくするために、ここでは固化した成形品は線形弾性の挙動を持ち、溶融樹脂は単に粘性の挙動を持つものとします。
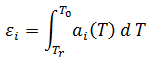
ここで、
-
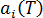は温度 T における第 i 主方向の線形熱膨張係数(CTE)。 - T0 は局部キャビティ圧力が大気圧に到達時の温度。この値は流動シミュレーションから得られる。
- Tr は室温
3D 流動シミュレーションでは、4 ノードの 1 次四面体要素の使用が適切です。ただし、通常の薄肉成形品や複雑な 3 次元成形品の薄肉領域の反り解析で 1 次四面体要素を使用すると、よく知られているシアーロッキングの問題により、構造的応答がきわめて剛になります [1]。シアーロッキングの発生原因は、線形四面体要素の線形変位場での精度不足です。アスペクト比の大きな要素を使用することで、シアーロッキングの影響は大きくなります。一方で、演算処理のコストを軽減するために、高アスペクト比を持つ四面体要素の使用が避けられないこともあります。したがって、射出成形品の薄肉領域に対しては、1 次四面体要素の使用は適切ではありません。
3D 反り解析のために、ハイブリッド要素スキームが考案されています。このスキームでは、3D ソリッド領域に 4 ノードの 1 次四面体要素を使用し、薄肉領域に 10 ノードの 2 次四面体要素を使用します。薄肉領域と厚肉領域を接続する転移領域には、5 ノード～9 ノードの転移四面体要素を使用します。
通常、3D の反りシミュレーションには、長い計算時間が必要となります。これは特に要素数が膨大な場合や、大きな薄肉領域がある場合などに顕著です。必要なメモリ容量を低減し、計算時間を短縮するために、効率的な前提条件の共役勾配反復ソルバーが実装されています。
参考資料
[1] K.J. Bathe, Finite Element Procedures, Prentice Hall Inc.(1996).
[2] S.G.Advani and C.L.Tucker III, The Use of Tensors to Describe and Predict Fiber Orientation in Short Fiber Composites, J. Rheol., 31,751-784(1987).
[3] G.P.Tandon and G.J.Weng, The Effect of Aspect Ratio of Inclusions on the Elastic Properties of Unidirectional Aligned Composites, Polym. Compos. 5(4),327-333(1984).
[4] R.A.Schapery, Thermal Expansion Coefficients of Composite Materials Based on Energy Principles.J. Compos. Mater., 2, No.3, 380-404, (1968).