応力結果の定義

次の結果から 1 つまたは複数を選択できます。

これらの結果の数学的定義は、任意の点における応力状態を示すよく知られているモールの円を使用して表すことができます。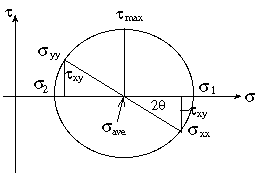

第 1 および第 2 主応力

主応力は垂直応力の極値です。主応力は、任意の点における応力の物理的状態の特徴を示し、基準座標とは無関係です。主応力は次のように計算されます。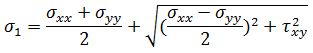

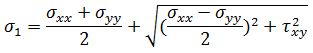
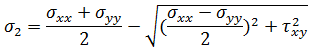
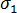ここで、

は最大垂直応力で、

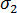は最小垂直応力です。主応力の対応する方向は、それぞれ第 1 主方向、第 2 主方向と呼ばれます。これらの角度は、次の式を使用して計算されます。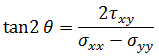

注: 主応力の正の値は引張を表し、負の値は圧縮を表します。

最大せん断応力はせん断応力の極値です。この値は次のように計算されます。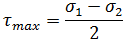

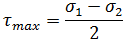
Mises-Hencky 応力は次のように計算されます。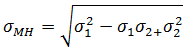

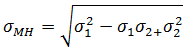
注: 上記の式で示されているように、Mises-Hencky 応力値は常に正の値になります。要素の中心から要素エッジへの外挿により、Mises-Hencky 応力で小さい負の値が生成されることがあります。この小さい負の値は、0 と同じであると見なされます。

通常、応力結果を調べる際には、成形品内の応力分布と成形品の最大応力レベルをチェックします。応力解析および反り解析では、要素の表側(肉厚方向表示位置 = 1)および裏側(肉厚方向表示位置 = -1)の両方の結果が出力されます。

これらの結果は、材料の推奨最大応力、および関連する成形品設計基準(例: 指定された破断基準など)がある場合はそれらの基準と比較する必要があります。

非充填の等方性材料は通常、次の図に示すようなぜい性または延性挙動を示します。図の (a) は脆性、(b) は延性の応力-歪挙動を表しています。

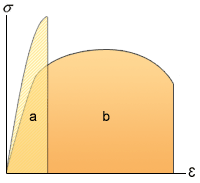
それぞれの場合で検討が必要な推奨応力結果は次のとおりです。

繊維充填異方性材料では、荷重下の成形品の挙動、破断の力学、および破断に関する設計基準が、等方性材料と比べて大幅に複雑になります。複合材料の応力解析、および取得された結果の解釈には、ユーザー側に特別な専門知識が必要となります。

繊維配向解析と応力/反り解析では、どちらも成形品肉厚方向のラミネートごとの結果が出力されます。

注: 主応力配向は、主繊維配向と一致しないことがあります。応力配向データは応力状態に依存し、各レイヤーの中央に位置します。繊維配向データは材料特性の 1 つで、レイヤーの境界で計算されます。