現在までに Autodesk Simulation Moldflow が反り解析で採用した収縮予測法は 2 種類あり、残留歪収縮予測法はその内の古い方になります。
MATHML ELEMENTS COMMENTED OUT. NEED TO REPLACE WITH IMAGE.
残留歪方法は、収縮を対象とした、次の実験的なモデルに基づいています。
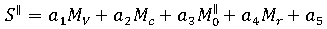
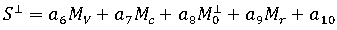
ここで、
-
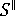 および
および 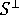 : 流動方向に平行な線形収縮の予測値、および流動方向に垂直な線形収縮の予測値
: 流動方向に平行な線形収縮の予測値、および流動方向に垂直な線形収縮の予測値 - a...a10: 所定の材料に対する定数
- MV: 体積収縮の指標
- Mc は結晶化の指標
-
 、
、 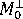 : 流動方向に平行な分子配向の指標、および流動方向に垂直な分子配向の指標
: 流動方向に平行な分子配向の指標、および流動方向に垂直な分子配向の指標 - Mr は金型拘束の指標
係数 a...a10 は、所定の材料に対する定数で、収縮特性決定手順によって決まります。この手順では、標準的な試験片の成形から得られた収縮データを、上記の式に適合させます。
モデル、体積収縮、結晶化、材料配向、および金型拘束のさまざまな指標は、所定の反りシミュレーションに対する充填+保圧解析で計算されます。これらの指標については、以降のセクションで詳細に説明します。
上記の収縮モデルは、金型の片側から反対側への温度差による曲げモーメントを説明するために、拡張されています。この温度差は、冷却解析から決定されます。これらの効果を組み込むことで、各要素の表側および裏側における流動方向に平行および垂直な収縮が与えられます。モデルのこの側面については、下記のセクション「金型拘束条件」で説明します。
体積収縮条件
体積収縮は、収縮計算の基本的な部分です。体積収縮に影響を与える主な要因は、保圧と、溶融の温度履歴です。各要素の体積収縮は、保圧と冷却中に発生した温度および圧力の履歴を使用して、材料に関する"平衡" pvT 関係から計算されます。
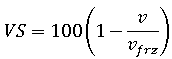
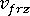 は要素内の樹脂が完全に固化した時点、または、要素内の溶融樹脂圧力が大気圧になった時点の樹脂の比容積です。 は大気圧および室温での樹脂の比容積です。特定の圧力と温度における比容積は、pvT 関係を使用して計算します。
は要素内の樹脂が完全に固化した時点、または、要素内の溶融樹脂圧力が大気圧になった時点の樹脂の比容積です。 は大気圧および室温での樹脂の比容積です。特定の圧力と温度における比容積は、pvT 関係を使用して計算します。 結晶化条件
平衡 pvT データだけでは、結晶性材料の体積収縮を説明できません。これらの材料で発生する体積収縮の量は、結晶化の程度によっても異なります。成形品の結晶化の程度は、主に、金型温度の影響を受けます。収縮計算では、材料の結晶化反応速度論を使用して、結晶化度による体積収縮を決定します。
結晶化は、温度と時間の両方の関数です。結晶化のレベルは、冷却速度によって決まります。内部の結晶化のレベルは、冷却速度が速いと低下し、冷却速度が遅いと上昇します。
射出成形品の厚肉部は、薄肉部と比較して冷却に時間がかかるため、内部の結晶含有量と体積収縮度が高くなります。一方、薄い部分は、非常に速く冷却されるため、中身の結晶化のレベルが低くなり、したがって、体積収縮の程度は、平衡 pvT データから予測されるよりも低くなります。
配向条件
せん断流れでは、ポリマー分子自体が、流動方向に沿って整列します。この配向の程度は、材料のせん断速度と溶融樹脂温度に左右されます。
樹脂流動が停止すると、誘発された分子の配向が、材料の緩和時間に依存する速度で緩和を開始します。緩和が完了する前に材料が固化すると、分子の配向は"凍結"します。この凍結した配向の結果、材料の配向の向きに平行および垂直な方向に、さまざまなレベルの収縮が起こります。
凍結した配向のレベルを判定するために、充填+保圧解析では、各要素およびその要素全体の各グリッド点 i について、そのグリッド点の固化時点における以下の量を計算します。
- せん断応力
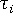
- 冷却速度
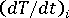
- 流動角度
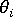 (要素のローカルな X 軸に対する流動角度)。このローカルな X 軸は、要素の定義における、最初のノード番号から 2 番目のノード番号への方向。流動方向は、ラミネートによって異なる場合がある。これは、固化層の増大によって流路が変わり、流動方向が変わる可能性があるため。
(要素のローカルな X 軸に対する流動角度)。このローカルな X 軸は、要素の定義における、最初のノード番号から 2 番目のノード番号への方向。流動方向は、ラミネートによって異なる場合がある。これは、固化層の増大によって流路が変わり、流動方向が変わる可能性があるため。
"凍結した"配向の最終的なレベルを決定するには、まず、樹脂流動が止まった時点での、せん断応力に比例する分子配向レベルを計算に入れます。次に、冷却速度の関数である、材料の緩和特性によって決まる量の分だけ配向のレベルを下げます。
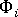 が決まると、 グリッド点 i およびローカルな X 軸に平行方向での配向の指標
が決まると、 グリッド点 i およびローカルな X 軸に平行方向での配向の指標 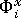 は、次の式によって算出されます。
は、次の式によって算出されます。 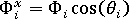
垂直方向の配向の指標 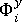 は、同様の方法で決定されます。
は、同様の方法で決定されます。
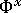 および
および 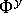 は、次の式に示すように、各グリッド点の指標を合計することによって決まります。
は、次の式に示すように、各グリッド点の指標を合計することによって決まります。 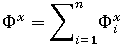
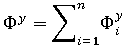
ここで、n はプラスチックのグリッド点の数
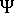 は、次のように定義されます。
は、次のように定義されます。 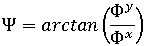
金型拘束条件
成形品が金型の中にある間は、要素の平面で物理的な収縮は発生しないと仮定します。ただし、肉厚方向の収縮は可能です。
材料が収縮すると、成形品には残留応力が発生します。充填過程、保圧過程、および冷却過程中のプラスチック要素の温度履歴は、これらの応力が緩和する速度に影響を与えます。金型拘束の指標は、多数の微小な温度増分からの寄与分を追加することにより計算されます。ここで、緩和の速度は、現在の温度から決定されます。
等価な熱歪
上述した残留歪収縮モデルにより、各要素に対して、平行および垂直な収縮の値が与えられます。この値は、この要素の肉厚全体の平均値を表します。実際には、収縮のレベルは肉厚によって変動します。この収縮の分布が、キャビティ中心線に関して非対称である場合、曲げモーメントが発生し、成形品の反りに影響することがあります。
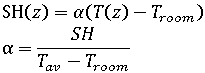
ここで、
T(z) は、中心が固化した時点、つまり、要素が完全に固化した時点で冷却解析から得られる、プラスチックの温度分布です。T(z) のピーク値は、材料の固化温度であり、要素の厚み方向の位置に現れます。これは、冷却解析から決定されます。上記の式を評価する際、金型とキャビティの境界における温度は、サイクル完了時の金型温度となるように近似され、最高温度の両側の温度分布は、放物曲線で近似されます。
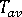 は肉厚方向における T(z) の平均
は肉厚方向における T(z) の平均
SH は収縮モデルにより予測される平均収縮
SH(z) は熱膨張の"実効"係数。これは、真の熱膨張係数ではありません。結晶化度など、他の収縮プロセスの効果が含まれているからです。
この SH(z) 分布は、この分布の曲げ効果を保持するように、線形化、つまり直線に変換されています。曲げ効果は、次の積分で表されます。
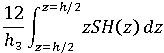
ここで、h は要素の厚み
この直線への変換は、近似ではなく、必然的なものです。その理由は、(ほとんどの応力解析プログラムと同様に) Autodesk Simulation Moldflow 応力解析プログラムでサポートされている要素のタイプでは、要素の肉厚方向における歪の線形分布しか扱えないためです。
この線形化の結果が、直線の収縮分布 SHL(z) です。これを、上記の式を使用して変換し、線形化された温度分布 TL(z) に戻します。変換して温度分布に戻す理由は、これまでの経緯にあります。つまり、Abaqus では、熱膨張と温度変化の係数のみを受け入れ、直接的な初期歪の入力を受け入れないことが一因です。
TL(z) から決定される要素の表側と裏側の温度、室温、および、平行および垂直な方向に対する 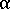 の値が、反り解析用の入力として保存されます。反り解析では、このセクションの最初に示した 2 つの式を使用して、これらの値から SHL(z) が再構築されます。
の値が、反り解析用の入力として保存されます。反り解析では、このセクションの最初に示した 2 つの式を使用して、これらの値から SHL(z) が再構築されます。