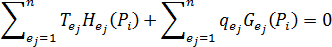冷却解析は、完全 3D 金型冷却解析です。冷却解析では、BEM(境界要素法)を基に開発された、数値的な手法が使用されます。BEM では、物理的な観点から、解を求めるときにすべての境界を熱源(取得熱/損失熱)と見なします。
金型の温度は、すべての熱源の影響を総合して決定されます。
3D 金型の平衡温度場は、ラプラスの式によって次のように表現することができます。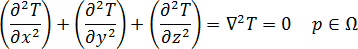
ここで、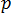 
について上式が成り立つものとします。この場合、境界条件は次のように統合されます。
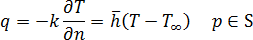
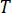は温度 
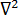はラプラス演算子 
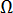は金型の内部および表面の領域
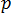について上式が成り立つものとします。この場合、境界条件は次のように統合されます。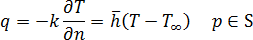ここで、
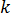は金型材料の熱伝導率 
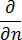は金型境界の外向きの法線微分 
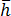は金型境界の等価熱伝達係数 
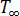は周囲環境の等価温度 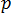- は特定の点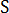
は金型表面(境界)
BEM ですべての境界条件が、金型温度場の解法にどのように適用されるか理解するため、まず、重みつき残差式について確認しましょう。
ここで、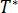
は重み関数です。
グリーンの第 2 等式を利用すると、式(3)は次の形式に変換することができます。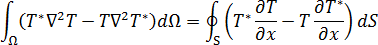
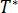を 次のように定義された式 (1)の基本解として選択します。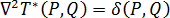
ここで、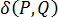
はディラックのデルタ関数です。3D 金型では、次のようになります。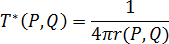
ここで、
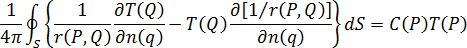
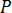と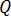 
は空間の 2 つの点であり、 
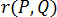はこれらの 2 点間の距離を表します。
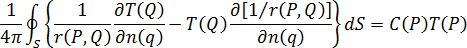
ここで、
、 
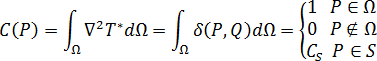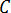は、立体内角に比例する定数です。
式(7)で、境界積分のみの式となりました。そのため、すべての金型表面(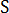)を 
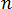個の要素に分割した場合、温度と温度変化が各境界要素で一定であると仮定すると、式(7)は次の形式に離散化することができます。
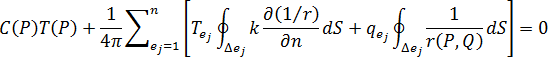
ここで、
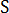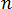)を 個の要素に分割した場合、温度と温度変化が各境界要素で一定であると仮定すると、式(7)は次の形式に離散化することができます。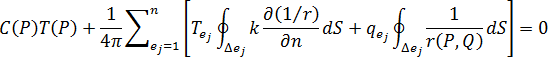ここで、
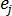は特定の要素 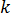- は金型材料の熱伝導率
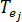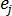は要素 の温度
温度作用項(いわゆる H 項)は、要素 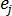の 点 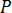に対する、温度の影響の強さを表し、次の式で計算されます。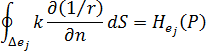
熱流束作用項(いわゆる G 項)は、要素 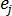の 点 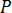に対する、熱流束入力の影響の強さを表し、次の式で計算されます。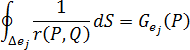
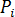が要素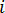 
の重心であると仮定します。式(9)の 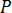に 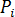を代入すると、次のような 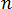個の線形方程式を得ることができます。