2 方程式乱流モデル(TKE & TED)

Autodesk Simulation CFD のいくつかの乱流モデルは、2 方程式モデルを使用して渦粘性係数と交換係数を決定します。2方程式によって、乱流運動エネルギーの輸送量Kと乱流エネルギー散逸量εを記述します。渦粘性係数および交換係数は、次の式を用いて計算されます。

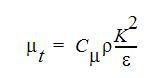
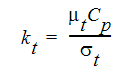
ここで、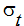は乱流プラントル数で、通常は1.0となります。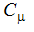は実験定数です。Kと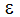に関する輸送方程式は、運動量方程式のモーメントを使用して以下のように導かれます。既定の高レイノルズ数 k-ε乱流モデルでは、次のようになります。

乱流運動エネルギー(TKE)方程式:

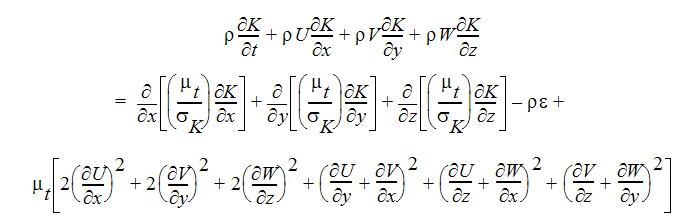
乱流エネルギー消失率(TED)方程式:

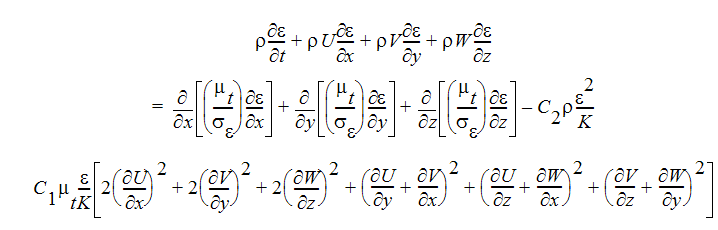
ここで、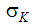と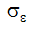は乱流シュミット数、C1とC2は実験定数です。このモデルに関連する、モデル化された全ての定数を下表に示します。これら 2 つの方程式により、9 つの未知数について 9 つの方程式が与えられます。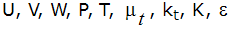

一定	値	Autodesk Simulation CFD の名前	値の増加による結果
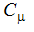
	0.09	CMu	混合、せん断、圧力変化の度合いが増大する。
C1	1.44	CE1	混合、せん断、圧力変化の度合いが減少する。
C2	1.92	CE2	混合、せん断、圧力変化の度合いが増大する。
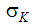
	1.0		（ユーザーによる変更不可）
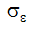
	1.3		（ユーザーによる変更不可）

前述の2方程式乱流モデルが、多くの事例に対して使用されており、一般的にほとんどの工学アプリケーションにおいて非常に有効です。しかし、この乱流モデルは、時に要求されるほど正確に剥離点を予測しません。解析を大幅に複雑化することなく、剥離離点をより正確に予測し、通常は解析の性能を高めるため、Autodesk Simulation CFD では RNG 2 方程式モデルという別の 2 方程式モデルを利用することができます。このモデルにおいて、運動方程式は波数空間に変換され、渦粘性モデルの計算を行う方程式を導くために、くりこみ群理論が使用されます。導かれた方程式は、より安定した理論上の基盤を持つため、RNGモデルを用いた結果は通常、さらに正確です。しかし、このモデルは数値的な安定性に劣り、その結果、収束がより困難になります。元の2方程式によって解析を開始し、その後ある時点より、RNGモデルを使用するのが最善の方法です。

また、RNG乱流モデルは、渦粘性乱流モデルでもあります。乱流運動エネルギーと乱流の消失率は、前述と同様に計算されます。2つの乱流モデルの違いは、上記の表に示した定数の決定方法にあります。次の式を用いて計算されたC1とともに、RNGモデルに対する値を下表に示します。

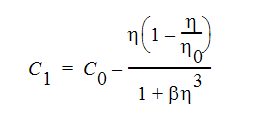
ここで、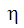は以下のように定義されます。

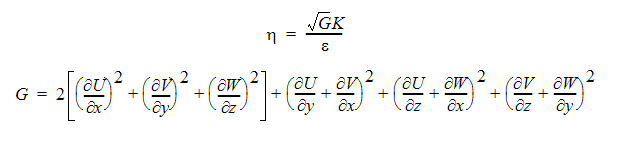
一定	値	Autodesk Simulation CFD の名前	値の増加による結果
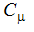
	0.085	CMu	混合、せん断、圧力変化の度合いが増大する。
C0	1.42	RNG CE0	混合、せん断、圧力変化の度合いが減少する。
C2	1.68	CE2	混合、せん断、圧力変化の度合いが増大する。
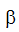
	0.015	RNGベータ	混合、せん断、圧力変化の度合いが増大する。
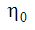
	4.38	RNG Eta	混合、せん断、圧力変化の度合いが増大する。
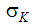
	0.7179		（ユーザーによる変更不可）
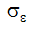
	0.7179		（ユーザーによる変更不可）

上に述べた2つの乱流モデルは、高レイノルズ数の流れや乱流が支配的な流れの計算に適しています。しかし、流れの大部分が層流である場合、開始時は乱流が支配的であっても終了時は層流で支配的である場合、その逆の場合には精度が落ちます。この精度低下は、広い空間での範囲の広いよどみ点付近の層流や、障害物周囲の境界層内の層流にはあてはまりません。このようなケースでは、低レイノルズ数乱流モデルが適しています。低レイノルズ数乱流モデルにおいても、Autodesk Simulation CFD は K とεについて 2 方程式モデルを使用します。K についての運動方程式は次のようになります：

乱流運動エネルギー方程式:

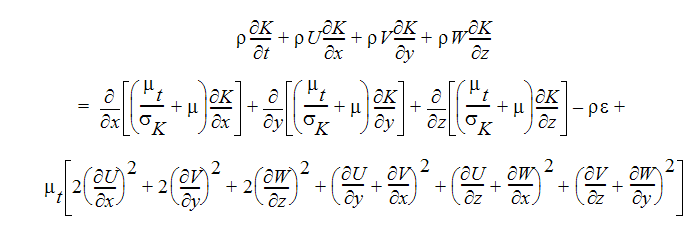
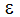についての方程式は次のようになります。

乱流エネルギー消失率方程式:

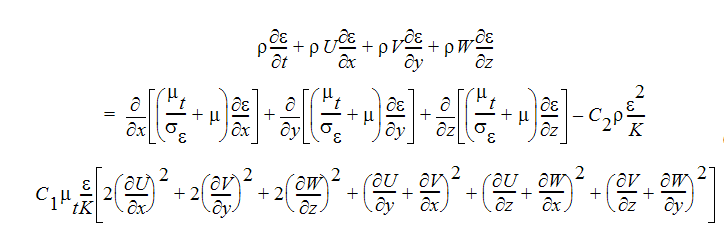
上記2式に含まれる定数は、以下の2つを除き既に説明したものと同じです。

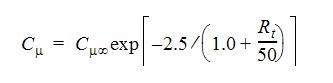
ここで、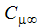は高レイノルズ数モデルと同じです。Rt は乱流レイノルズ数です。

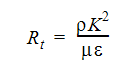
もう1つは次の通りです。

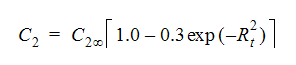
ここで、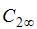は高レイノルズ数モデルと同じであり、Rt は乱流レイノルズ数です。

流入境界条件

Kおよびεについて、流入口境界条件を指定する必要があります。利用可能な値が存在する場合は非常に少ないと言えます。ほとんどの実用アプリケーションにおいて、利用可能な値は存在せず、推定値を求めなければならなりません。このような推定値を求めるため、いくつかの定義が必要となります。

乱流運動エネルギーは、以下のように定義されます。

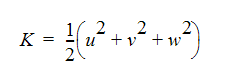
ここで、この方程式における流速は、流速の変動分です。乱流強度は以下のように定義されます。

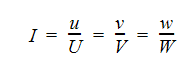
上記2つの方程式の組合せにより、流入口の流速分布に基づいた、流入口における乱流運動エネルギーの推定値が求められます。

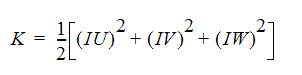
乱流強度については、より頻繁に利用可能な値が存在し、より容易に予測することができます。この値は、解析ダイアログの乱流ボタンを使用して入力できます。これは「強度因子」としてリストアップされます。内部流れに対するデフォルト値は5％、外部流れに対するデフォルト値は1％です。旋回流など、流入する流れがはっきりと乱流である場合、デフォルト値の代わりに10～20％ほど高い値が設定される場合があります。多くの内部流れ問題において、局所的なせん断力が乱流量を左右する場合、流入口の値は下流に対して大きな影響力を持ちません。

乱流エネルギー消失率は、次のような長さスケールの項に関して定義されます。

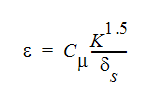
ここで、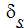は長さスケールです。長さスケールは Autodesk Simulation CFD が自動計算します。内部流れか外部流れかによって、異なる長さスケールが使われます。Autodesk Simulation CFD は内部流れ(壁面が多い)か、外部流れ(壁面が少ない)かの決定も自動で行います。

壁モデル

前項において説明した乱流モデルは、ともに「高レイノルズ数」モデルです。つまり、それらのモデルは、完全な乱流の型においてのみ厳密に適用することができ、境界層の内部層には適用されません。前述の低レイノルズ数モデルは、すべて滑りのない壁面に適用されます。したがって、低レイノルズ数乱流モデルは、境界層や再層流化領域にも適用できます。低レイノルズ数モデルにおいては、いくつかの節点（3～10）を境界層（y+値1～5）内に配置する必要があります。メッシュエンハンスメントにより、この基準はほぼ満足することができます。Autodesk Simulation CFD

高レイノルズ数モデルでは、壁近傍の乱流をモデル化する方法として壁関数を使用します。「壁関数」は、壁要素における乱流モデルに代わり、一般的に境界層において1つの節点のみの配置を要求します。高レイノルズ数乱流モデルとともに壁関数を使用する方法は、ほとんどの乱流に対して有効です。

「壁関数」の主な目的は、壁法則を適用することです。次のように表されます。

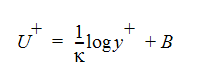
ここで、Bと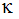は無次元定数です。内部変数のU+とy+は、以下のように定義されます。

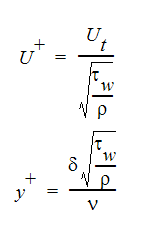
ここで、Utは壁に対する流速、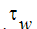は壁面せん断応力、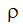は密度、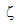は壁からの距離、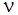は動粘性係数です。Autodesk Simulation CFD は、壁の法則を適用するため、壁近傍の流速と流体特性に基づき、壁面有効粘性係数を変更します。分離流れを除き、壁の法則は、以下の範囲において非常に有効です。

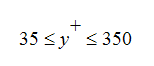
Autodesk Simulation CFD によって計算される y+ の値は、ポスト処理ファイルに出力されるため、プロットすることができます。Autodesk Simulation CFD により実行されたいくつかの検証問題について、内部流れにおける圧力損失の推定値が過小である場合、y+ の値が 35 より小さくなるということが分かっています。内部流れにおける圧力損失の推定値が過大となりました。y+の値は350より大きい場合、また、特にその境界において一様流速が指定される場合など、流入口付近において、y+の値がこの範囲外になることがあります。

粗い壁の場合、壁の法則は以下のように変更されます。

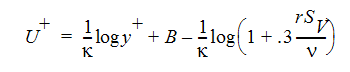
ここで、rは、壁から測定された 粗さの平均高さ （長さ単位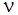）、は動粘性係数、S v はせん断速度です。rのデフォルト値は0.0であるため、付加された粗さの項は結果的に消失します。この値は、材料物性ウィンドウを使って設定します。CFdesignにおいて入力された値が全ての壁に対して使用されることに注意してください。

変更可能な壁定数とそのデフォルト値を下表に示します。

一定	値	Autodesk Simulation CFD の名前	値の増加による結果
A+	26.0	VanDriest	壁境界層における温度混合の度合いが減少する。
B	5.50	壁面パラメータ	壁せん断、圧力変化の度合いが減少する。
r	0.0	表面粗さ	壁せん断、圧力変化の度合いが増大する。
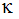
	0.40	Kappa	壁せん断、圧力変化の度合いが増大する。

乱流伝熱問題に対し、温度の壁法則が適用されます。乱流プラントル数と層流プラントル数の相対的な値に応じて、Autodesk Simulation CFD は 2 つの異なる形式の関係式を使用します。2つの方程式の違いは、式が壁近傍の渦粘性分布の置き換え表現方法です。1番目のケースにおいては、Spalding's Inner Law [1]を使用して、次式で計算されます。

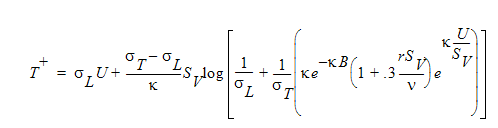
ここで、σ L は層流プラントル数、σ T は乱流プラントル数です。層流プラントル数は次の通りです。

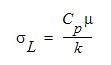
ここで、Cp は比熱、μは絶対粘度、kは熱伝導率です。T+は以下のように定義されます。

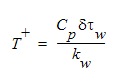
ここで、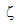は壁からの距離、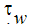は壁面せん断応力、kw は壁法則適用範囲における熱伝導率です。壁面温度の法則に関するこの式は、層流プラントル数が乱流プラントル数(Autodesk Simulation CFD によって 1.0 の値が割り当てられる)より小さい場合に使用されます。したがって、ほとんどの空気またはガスには、この式を使用します。

層流プラントル数がより大きな流れ（水など）の場合、温度の壁法則について、渦粘性係数に関するVan Driest の式が使用され、次式が与えられます。

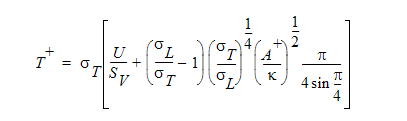
ここで、A+はVan Driestの定数です。この定数には、Autodesk Simulation CFD によって 26.0 の値が割り当てられています。これは、解析タスクの乱流ボタンをクリックし、乱流ダイアログのアドバンストボタンをクリックして変更することができます。