移動固体のモデリングの背景に存在する概念は、どちらかと言えば単純です。固体と接触する流体は接点で瞬間的に速度を持つと仮定されます。言い換えれば、この状態に、非スリップ境界条件を適用します。
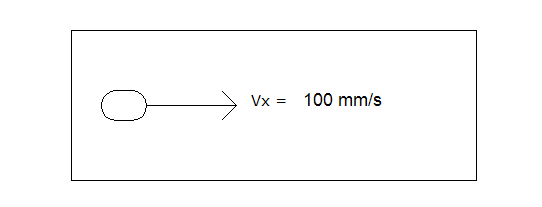
例えば、下図において、発射体が左から右に向かって100 mm/秒で移動しています。つまり、固体表面に沿った流体には、時間ステップごとに100 mm/秒の流速が指定されます。
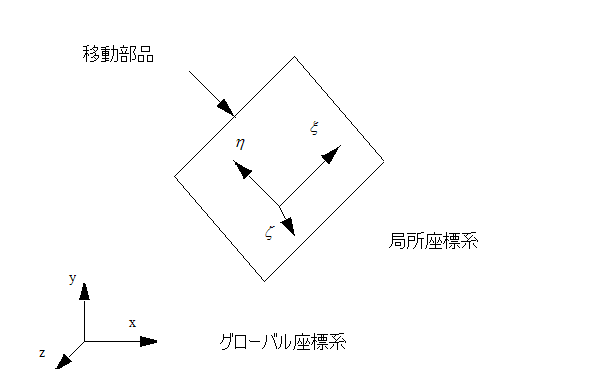
任意の動きを可能にするため、それぞれの移動部品内にローカル座標系を設定します。部品はこのローカル座標系に対し移動しないものと仮定されます。正確に言えば、ローカル座標系は、グローバル座標系と相対的に移動します。
移動固体上の任意の点(x,y,z)におけるグローバル座標上の点は、以下のような変換によって計算することができます。
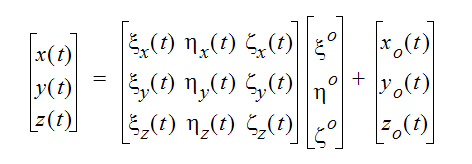
ここで、(x,y,z)は、任意の時間(t)において計算されたグローバル座標値です。
-
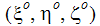 は、移動部品のローカル座標系での座標値です。時間ゼロにおいて1回のみ計算されることを示すため、これらの座標値には上付き文字oが付けられます。定義により、これらは時間的に不変です。
は、移動部品のローカル座標系での座標値です。時間ゼロにおいて1回のみ計算されることを示すため、これらの座標値には上付き文字oが付けられます。定義により、これらは時間的に不変です。 -
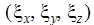 は、ローカルx軸の成分です。
は、ローカルx軸の成分です。 -
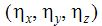 は、ローカルy軸の成分です。
は、ローカルy軸の成分です。 -
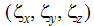 はローカルz軸の成分です。
はローカルz軸の成分です。 -
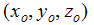 は、ローカル座標系の原点のグローバル座標上の位置です。
は、ローカル座標系の原点のグローバル座標上の位置です。
時間レベルごとに新しいメッシュを作成する代わりに、固体メッシュは流体メッシュ中を突き抜けることができます。流体ノードが固体の要素によって「覆われた」際、最も近い固体ノードの速度が、覆われた流体ノードに適用されます。ここに提示する図においては、矢印が指示する流体ノードが、移動部品の角の固体要素によって覆われています。移動境界内にある全ての流体ノードは「覆われ」、移動固体によって速度が制御されると仮定されます。
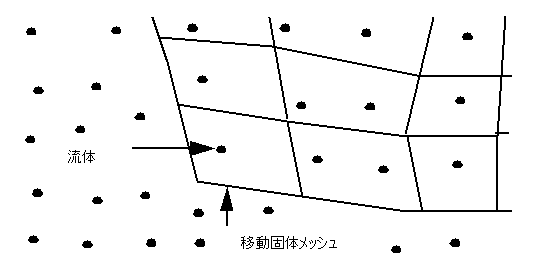
モデルを最初に作成する際に、これらの移動固体は流体に埋め込まれます。固体の移動開始後、固体が移動した後の領域は流体領域とならなければなりません。この設定に対応するため、流体と接触するように作成された全ての固体には、流体の要素およびノードが自動的に追加されます。この機能を複製と呼びます。流体領域の外側に移動固体が存在するようなモデルを作成する場合、複製は行われません。
直線運動
直線運動は、以下に図示するように与えられた方向に沿った運動です。
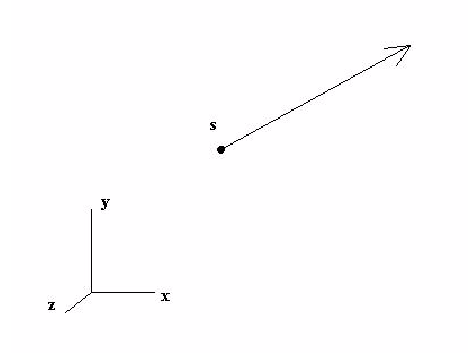
変位(sで表示された) は、物体の初期位置から相対的に測定されます。ユーザーは、sを軌跡パスに沿って移動する物体の時間の関数として定義できます。軌跡は、単位方向ベクトル(Ux, Uy, Uz)を使用して定義されます。グローバル座標系で定義された運動は次式で表されます。
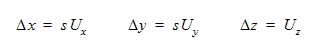
直線運動が流体力による運動の場合、グローバル座標系で計算されたせん断力と圧力は内積を使用してs方向に適用されます。
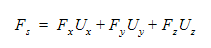
この力のために、一定の力とばね力を追加することができる。 運動の式は次式で表されます。
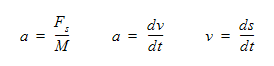
ここで、 aは加速度、M は質量、vは速度、sは変位、 tは時刻です。
回転運動
回転運動は、以下に示すように軸周りに回転する物体です。
物体の回転軸は、単位ベクトル(Ux, Uy, Uz)を使用して定義されます。回転中心は、指定点(Px, Py, Pz)で与えられます。回転量は、変数 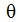 によって表されます。
によって表されます。
これは、物体の初期位置からの相対的な値です。局所座標系では、運動は 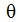 と時間の関係として表されます。
と時間の関係として表されます。
3次元で表記する場合、方向余弦を使用して運動を記述することが有効です。
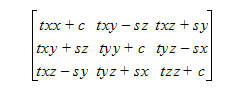
ここで、
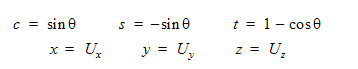
流体力による運動の場合、内積によって回転軸に対して作用するトルクが計算されます。
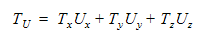
このトルクにユーザー指定のトルクを追加することもできます。運動は、次式で表されます。
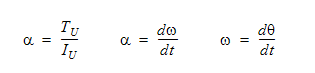
ここで、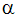 は回転加速度、Iu は回転ベクトルに対する回転慣性力、
は回転加速度、Iu は回転ベクトルに対する回転慣性力、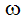 は角速度、
は角速度、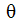 は回転位置、t は時刻を示します。
は回転位置、t は時刻を示します。
直線運動と回転運動の複合運動
前に説明した2つの運動を組み合わせることにより、複合運動を定義することができます。回転の中心は、s で与えられた経路に沿って運動します。回転は、局所的にはθ、グローバルには方向余弦で定義されます。直線運動が流れによって駆動される場合、流体力が運動方向に沿って作用する場合、線形的に加速される結果となります。
流体力による回転の場合、発生したトルクは回転加速度を計算するために使用されます。双方の運動が流体力によって駆動される場合、それぞれの運動は独立していると仮定され、個別に作用し、全体的な運動に寄与することになります。直線運動の方程式は、回転中心の時間的な移動とともに更新され、回転運動の方程式は、複合運動の作用する間、方向余弦を更新します。
周回運動と回転運動
周回運動とは、物体が時間とともに円周方向の軌跡に沿って運動することです。この状況を以下に示します。
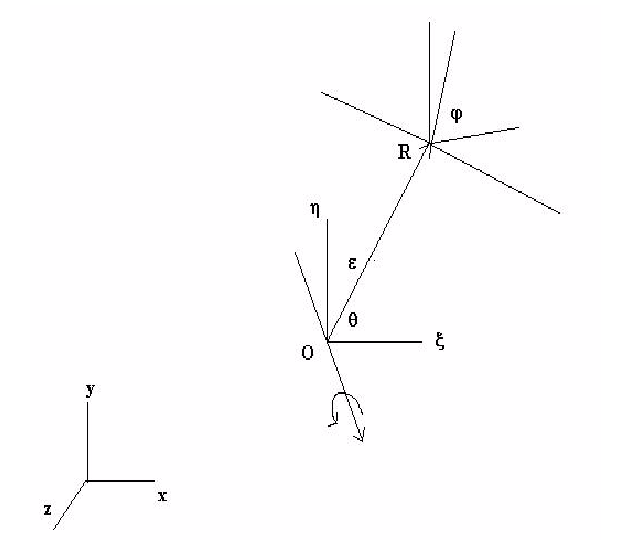
変数 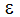 は周回運動の半径または偏心です。これは、点Oと点Rを使用して計算されます。
は周回運動の半径または偏心です。これは、点Oと点Rを使用して計算されます。
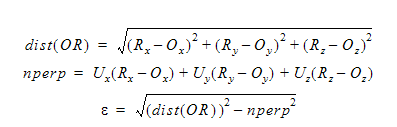
ここで、周回システムの原点と回転システムの回転軸間の垂直方向の距離を求めるため、非垂直方向ベクトルを差し引いています。周回システムの回転軸は、単位ベクトル(Ux, Uy, Uz)で表されます。
局所座標系では、周回は次式で与えられます。
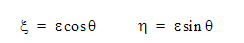
これは、回転変換マトリックスの構築によるグローバル参照フレームでは、以下のように記述されます。
- 局所 z 軸(
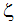 )は周期回転軸 U と同一と考えます。
)は周期回転軸 U と同一と考えます。 - 局所 x 軸(
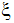 )は、時刻ゼロの回転システム原点と周回運動システムの原点から決定される単位ベクトルとします。
)は、時刻ゼロの回転システム原点と周回運動システムの原点から決定される単位ベクトルとします。 - 局所 y 軸(
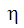 )は、局所 z 軸と局所 x 軸と直交する方向です。
)は、局所 z 軸と局所 x 軸と直交する方向です。 - 全ての局所座標軸が定義されれば、Gram-Schmidt法が、この局所座標系が真に直交していることを保証します。
グローバル周回座標位置は、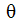 の関数として次の式で表されます。
の関数として次の式で表されます。
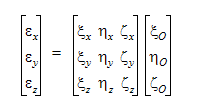
周回運動が流体力によって駆動される場合、物体に作用する力が合計され、適切な加速度が計算されます。速度と変位は、次の関係式を使用して周回パス上に制限されています。

周回運動の方程式は、運動する物体の変位を定義します。物体は、偏心ベクトルによって指定される点についても同様に回転することができます。既に開発された回転方程式がこの運動を記述します。
章動運動
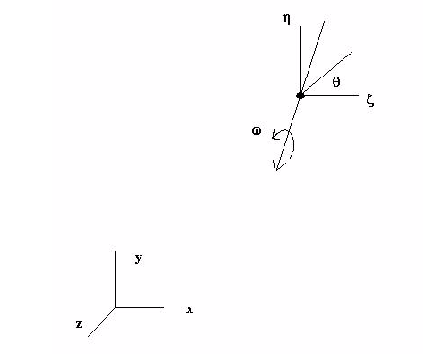
章動運動は、次の図を用いて説明できます。
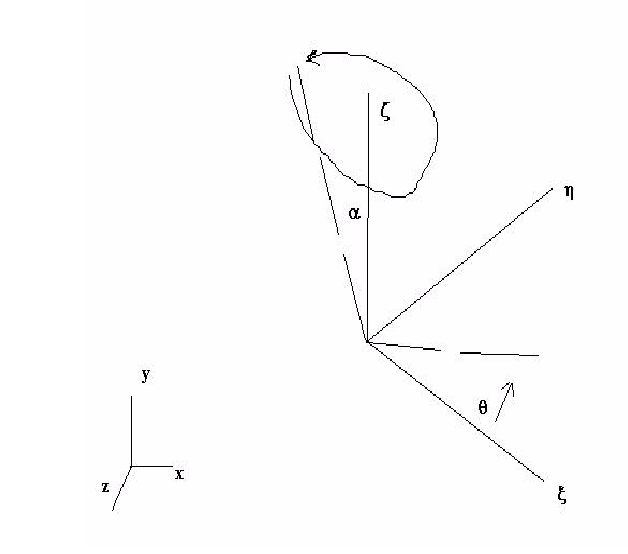
才差運動あるいは章動運動は、章動角度 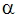 で定義されます。角度
で定義されます。角度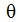 はz軸回りの回転角度を定義します。局所y軸は局所y平面とz平面において、運動の静止が許される場所(
はz軸回りの回転角度を定義します。局所y軸は局所y平面とz平面において、運動の静止が許される場所(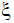 =0 )を定義します。局所空間では、方向余弦は以下で表されます。
=0 )を定義します。局所空間では、方向余弦は以下で表されます。
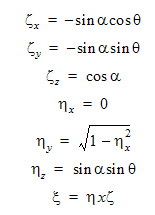
上述のように、変換マトリックスは、グローバル空間の方向余弦を作成するために使用されます。
章動運動が流体力によって駆動される場合、これより前に説明された回転運動に対して行われた方法と同様の手法にて、正味のトルクが回転加速度の計算に使用されます。
自由運動
これは、ここで説明されている非拘束の剛体運動の定式化を使用しています。