超弾性およびフォーム材料モデルの材料特性入力ダイアログ ウィンドウには、[カーブフィット]ルーチンが含まれます。 カーブ フィットは、材料に関するユーザ設定の応力-ひずみデータの最適フィット計算を実行することによって、数学的材料モデルの定数を特定する際に使用します。テスト データに正確にフィットする解はないことに留意してください!テストと材料におけるばらつきにより、テスト データにおける拡散がもたらされます。このため、曲線フィット ルーチンにおける高い精度は多くの状況で正当化されません。重要なことは、曲線フィット ルーチンの結果は、対象範囲のテスト データに従うという点です。
各材料モデルには、その必要性に特有のオプションがあります。以下に説明する項目のいくつかは、材料モデルによっては関連しません。[カーブフィット]ダイアログの一般的なレイアウトを図 1 に、説明を以下に示します。
|
|
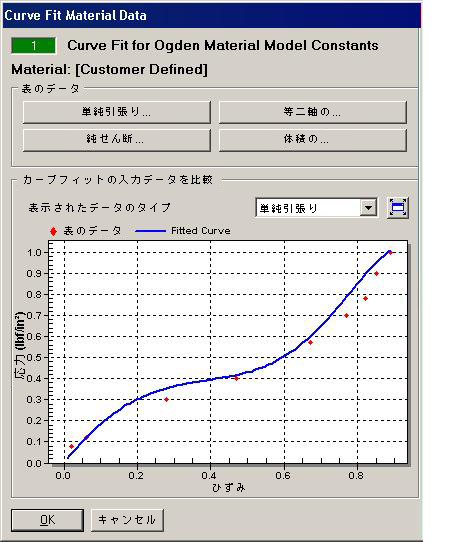
| 図 1L: Ogdenのカーブ フィット ダイアログ (ダイアログの左半分) |
|
|
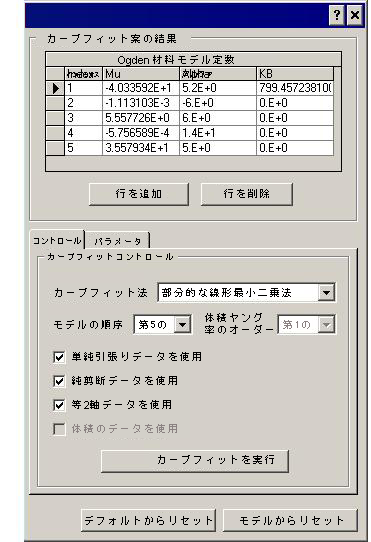
| 図 1R: Ogdenのカーブ フィット ダイアログ (ダイアログの右半分) |
表のデータ セクション:
このセクションは、材料に関する既知の応力-ひずみデータを入力するために使用されます。まず、テスト データの取得時には次の事項に留意することが重要です。
- 解析の正確な定数を生成するには、[カーブフィット]に入力される応力-ひずみデータで、その解析において生じるあらゆる範囲の負荷に対応できなければなりません。たとえば、パーツに引張および圧縮の他にせん断応力が生じる場合、純せん断応力-ひずみデータを入力する必要があります。単純引張は、それ自体、そのような状況において材料の挙動を適切にモデル化するのに十分ではありません。同じことが、その他の表のデータに該当します。
- 材料定数の生成には、すべての実験のデータがまとめて使用されるため、テストされる材料は同じバッチのものであることが重要です。これ以外の場合、材料生成におけるばらつきによりテスト データが歪みます。
- 多くのエラストマーによって、最初の数回の荷重繰返し時の挙動が変わります。また、応力-ひずみ曲線によって、最大ひずみがいつ増加するかが変わります。このため、材料は解析におけるひずみ予想値にサイクルする必要があり、荷重は挙動が安定するまで繰り返す必要があります。
- このような準備が整っていない場合は、応力-ひずみテスト データを 0 ひずみ条件にシフトする必要が生じることがあります。超弾性材料は、新しいひずみ速度まで伸長されると、多くの場合、元のひずみに戻らなくなります。(このことは、最初のサイクルにも、多くのサイクルの後にも該当します。新しいより高度なひずみ速度により、新しい永久変形がもたらされます。)テストで計測される永久変形はひずみ値から削除する必要があります。同様に、永久変形により変わる断面積は、応力の計算に使用される最初の領域内に反映される必要があります。これら 2 つの補正により、応力-ひずみ曲線が開始値の 0,0 に戻ります。
- 使用する材料モデルに応じて、超弾性材料モデルの多くは繰り返しの読み込みによって特性を変えることはありません。解析の各サイクルは、計算済みの応力-ひずみ曲線に従います。このため、テスト データは、解析挙動に合致するように選択または平均化される必要があります。
- 超弾性材料モデルのほとんどは、同一の応力-ひずみ曲線に従って読み込みおよび読み込み解除されます。永久変形はありません。
入力できるテスト データのタイプは次のとおりです。
- [単純引っ張り]ボタン:単純引張テストからの応力-ひずみデータを入力します。テスト データは、引張ひずみの純粋状態が計測されるようでなければなりません。テスト データに側面の拘束はありません。引張ブランチのみが入力されます。圧縮データは等二軸データから生成されます。
- [等二軸]ボタン: 等二軸伸張試験からの応力-ひずみデータを入力します。これは、圧縮応力-ひずみの再生成に使用されるテスト データです。2 方向に均等に引張ることで、純粋圧縮に相当するひずみ状態が作られます。
- [純せん断]ボタン:純せん断ひずみテストからの応力-ひずみデータを入力します。超弾性材料の場合、通常は広い引張標本となりますが、材料はほぼ非圧縮性であるため、純せん断状態が存在します。
- [単純せん断]ボタン:単純せん断テストからの応力-ひずみデータを入力します。
- [体積]ボタン:体積圧力テストからの圧力-ひずみデータを入力します。 このデータは、体積弾性率の特定に使用されます。超弾性材料の場合、これは、材料がわずかに圧縮可能である状況、あるいはパーツが高度に拘束されている状況において重要となります。通常、体積弾性率はせん断弾性率よりも大きい 2 つから 3 つの大きさのオーダです。フォーム材料の場合、体積データはフォームの圧縮可能性を捕捉するために重要です。
[表のデータ]セクションの任意のボタンをクリックすると、応力およびひずみデータが入力された新しいダイアログ ウィンドウが表示されます。使用できるコントロールは次のとおりです。
- [ひずみフォーマット]プルダウン:ひずみデータの形式を選択します。[公称ひずみ]は (長さの変更)/(元の長さ) から、[真ひずみ]は (現在の長さ)/(元の長さ) = 1+(公称ひずみ) から計算されます。
- [有効なポアソン比]フィールド(フォーム材料モデルのみ):ポアソン比が分かっており、横ひずみが不明である場合、有効なポアソン比の値を入力します。この入力は、ポピュレートボタン、および横ひずみ計算のためにスプレッドシートに入力される主ひずみと併せて使用されます。
- [ポピュレート]ボタン:このボタンをクリックすると、[有効なポアソン比]フィールド、[ひずみ]、[プライマリ]スプレッドシート列に基づき、スプレッドシートの[ひずみ]、[横向き]列の値が計算されます。
- [横方向の応力を入力]チェック ボックス:フォーム材料の場合、せん断応力および横向き応力に異なる値を設定できます。(単純せん断のテスト データにのみ表示される)このオプションがアクティブな場合、応力-ひずみスプレッドシートに横せん断応力が入力されます。オプションがアクティブでない場合、横せん断応力はせん断応力と同一と仮定され、列はスプレッドシートに含まれません。
- [応力-ひずみデータ]または[体積圧力ひずみデータ]スプレッドシート:要求応力およびひずみを入力します(データのタイプに応じる)。 (元の長さおよび領域に基づき、)公称応力およびひずみを使用する必要があります。値は 2 列目(通常は、超弾性材料のひずみ、およびフォーム材料の応力)に基づき、昇順で入力する必要があります。
- [自動修正]チェック ボックス:体積圧力ひずみデータの場合、体積弾性率を適切に計算するためには、ひずみおよび圧力の記号が適切である必要があります。 このオプションがアクティブな場合、適切な計算結果を得る必要があるときには、プロセッサでは入力体積圧力の記号が切り替えられます。このオプションがアクティブでない場合、ひずみ値を負の値に、圧力を正の値にする必要があります。
- [行を追加]および[行を削除]ボタン:それぞれ、スプレッドシートの最後への行の追加、現在の行の削除を行います。
- [ソート]ボタン: 応力-ひずみデータを、2 列目(通常は、超弾性材料のひずみ値、またはフォーム材料の応力値)に基づき、昇順で並べ替えます。
- [インポート]ボタン: カンマ区切り(CSV)ファイルから、応力-ひずみデータを読み込みます。データ ファイルはスプレッドシートと同じ形式である必要がありますが、[インデックス]列を伴いません。既存のデータは読み込まれたデータで置換されることに注意してください。フォーム材料モデルの場合、2 つまたは 3 つの列を読み込むことができます。3 列目([ひずみ]、[横向き])がカンマ区切り値ファイルに含まれていない場合、この列は 0 に設定されます。[有効なポアソン比]フィールドおよび[ポピュレート]ボタンを使用すると、概算値が作成されます。 重要: 応力-ひずみスプレッドシートの一部は 1 列目の応力を使用し、またいくつかはひずみを使用します。.CSV ファイルでは、データがスプレッドシートに対応する適切な列に存在している必要があります。ヒント: カンマ区切りファイルの値はアクティブな[表示単位]を使用して読み込まれます。データの読み込み前に、必要に応じて[表示単位]を変更します。たとえば、値 314 は、[表示単位]がポンドおよびインチに設定されている場合には 314 psi として読み込まれ、[表示単位]がニュートンおよびメートルの場合には 314 Pa として読み込まれます。
- [エクスポート]ボタン:入力された応力-ひずみデータをカンマ区切りファイルに保存します。
[パラメータ]タブ
一部の材料モデルは、最小二乗フィット ルーチンを開始するのに概算値または推定値を必要とします。これらのパラメータは[パラメータ]タブに、カーブ フィットの試行前に入力する必要があります。 入力するパラメータは[コントロール]タブで選択されたカーブ フィット法のアルゴリズムに応じて異なります。
[部分的な線形最小二乗法]:この検索方法によって、最初の推定値に基づくすべての可能な係数の組み合わせが計算され、エラーが最小となる組み合わせが報告されます。 すべての組み合わせが計算されるため、この方法は、特に大きな増分値が使用される場合にはその他の方法よりも時間を要することがあります。また、範囲外の解がテストされるため、小さなエラーを伴う解が存在することに注意してください。プロットされた結果がデータにフィットしない場合は、異なる範囲を試してください。入力は次のとおりです。
- [見積り]または[推定]値:パラメータの最初の推定値を入力します。 この入力は、実際には計算される範囲の中央になります。一部の材料モデルでは、いくつかの値で 0 は許容されないことに注意してください。 たとえば、Ogden 材料モデルのポテンシャル式では、分母にαパラメータを使用するため、0 による除算は許容されません。フィット ルーチンでこのようなことが生じる場合、パラメータは定義済みの既定値に切り替えられます。
- [範囲値]: テストする推定値の範囲を入力します(テストする最低値から最高値まで)。 最低値は範囲の半分を推定値から減算した値です。また、最高値は範囲の半分を推定値に加算した値です。
- [増分値]値:計算される最低値と最高値との間の点の数です。 このため、3 つのパラメータに対する増分 20 により、20^3 = 8000 の組み合わせが作られ、これらから最小エラーが報告されます。
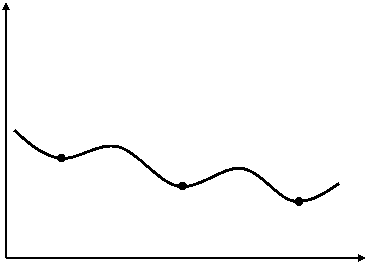
[Levenberg-Marquardtアルゴリズム]、[ガウス-ニュートンアルゴリズム]、および[拘束された最適化]:これらの方法は最初の推定値から開始され、最適フィットの計算式に対して最初の最小値(エラー関数の勾配は 0)を割り当てます。 複数の変数が使用されると数多くの最小値が生じることがあるため、解の精度は最初の推定値に依存します。図 2 を参照してください。
- [見積り]または[推定]値:定数それぞれの要求見積もり値を入力します。 値 0 は使用しないことをお勧めします。また、モデルのオーダの各推定値には何らかの値を入力する必要があります。第 5 オーダのモデルを計算する場合、最初の 5 つの定数について見積もり値を入力する必要があります。別のカーブ フィッティング法による結果が適切な見積もり値となります。例として、部分的な線形最小二乗法を使用して見つけられた定数は、Levenberg-Marquardtアルゴリズムの適切な見積もり値となります。カーブ フィットは数値解法であるため、見積もり値が異なるとカーブ フィットの結果も異なります。
- [最大反復]フィールド:使用する反復の最大数を入力します。反復の最大数に達する前に解が見つからない場合は、カーブ フィッティング ルーチンでエラーが生じます。
- [許容誤差]フィールド:カーブ フィッティング ルーチンに使用する許容誤差を入力します。 解は、それぞれの定数がある反復から次の反復へ、許容誤差よりも小さい値で変化する際に収束すると考えられています。
|
エラー |
[コントロール]タブ
[カーブフィットコントロール]セクション:
カーブフィット コントロールは、テスト データがカーブ フィッティング ルーチンでどのように使用されるか(カーブ フィット計算にどのテスト データを含めるか、モデルのオーダ、データのフィッティング方法など)を示すために使用されます。
- [データを使用]チェック ボックス:カーブ フィッティング ルーチンで使用するテスト データのチェック ボックスをアクティブにします。 入力されるすべてのテスト データを使用する必要があります。特定のデータ セットを使用しない理由は、特定のセットによってその他のデータに良好にフィットしなくなるためです。この場合、異なるモデルのオーダ、異なるカーブ フィッティング法、または材料モデルを使用して、より良好なフィットを得る必要があります。
- [カーブフィット法]ドロップダウン:テスト データへの最適フィットを見つけるための数値的技法を選択します。 各技法によって異なる定数セットが示されます。(視覚的および RMS 内の)データへの良好なフィットをもたらす方法を使用します。[Levenberg-Marquardtアルゴリズム]および[ガウス-ニュートンアルゴリズム]は、最初の見積もり値に影響を受けることがあります。これらは[パラメータ]タブに入力します。[部分的な線形最小二乗法]法は、定数の最初の見積もり値を見つけることに適しています。
- [モデルのオーダ]プルダウン:カーブフィット ルーチンのモデルのオーダを選択します。 一般に、オーダが低いほど解析が早くなりますが、オーダの高いモデルには、特に応力-ひずみ曲線の変曲が比較的大きい場合などにテスト データへのより良好なフィットが求められます。
- [体積弾性率オーダ]プルダウン:カーブ フィッティング ルーチンの体積弾性率計算のオーダを選択します。オーダが高いほどテスト データへのフィットがより正確になります。いくつかの材料モデルでは、体積テスト データが与えられない限り、この値を見積もることはできません。また、体積テスト データが入力され、カーブ フィットで使用されない限り、このエントリを既定の 1 定数にする材料モデルもあります。
- [カーブ フィットを実行]ボタン:このボタンをクリックすると、カーブ フィット演算が開始されます。 [カーブ フィッティング処理]ダイアログが表示されます。[フィット]ボタンをクリックして、反復処理を開始します。処理に成功した場合、カーブ フィットの精度(二乗平均平方根)が示されます。値が小さいほど、選択されたデータへのフィットがより正確であることを示します。処理に失敗した場合、[パラメータ]タブで最初の推定値を変更して、カーブ フィットを再試行します。 注: カーブ フィッティングでは、材料定数の決定に、さまざまな最小二乗フィッティング アルゴリズムが使用されます。このため、さまざまな数値的技法および入力パラメータにより、異なる解が得られることがあります。値を微調整することにより、異なるカーブ フィットが得られることがあります。テスト データには制御不能な要因によるばらつきが含まれるため、カーブ フィッティング ルーチンにおける相違は通常は無視できます。(カーブ フィッティング法の詳細については、数値的方法のテキストブックまたは Web サイトを参照してください。)
[カーブフィット案の結果]セクション
このセクションには、カーブ フィッティングにより計算される材料モデル定数が示されます。定数がデータへのフィットに与える影響を確認するには、値を変更して、[表示されたデータのタイプ]を選択してグラフを更新します。
これらの値は、[OK]ボタンをクリックして[カーブ フィット材料データ]ウィンドウを閉じると、[カーブ フィット材料データ]ウィンドウから[要素の材料指定]ウィンドウにコピーされます。
さまざまな材料モデルで次の計算式が使用されます。
- Neo-Hookean
- 等軸: T u = stress = 2(λ u - λ u -2 )C 10 where I 1 = λ u 2 + 2λ u -1
- 等二軸: T B = stress = 2(λ B -λ B -5 )C 10 where I 1 = 2λ B 2 + λ B -4
- 純せん断: T S = stress = 2(λ S -λ S -3 )C 10 where I 1 =λ S 2 + 1 + λ S -2
- 体積: p = pressure = -K(J-1) where J = λ v 3
- where λ = stretch = 1 + strain
- Van der Waals:
- 等軸: where I 1 =λ u 2 + 2λ u -1 and I 2 =λ u -2 + 2λ u
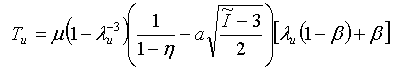
- 等二軸: where I 1 = 2λ B 2 + λ B -4 and I 2 = 2λ B -2 + λ B 4
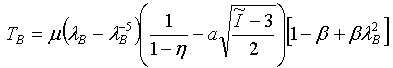
- 純せん断: where I 1 =λ S 2 + 1 + λ S -2 and I 2 =λ S 2 + 1 + λ S -2
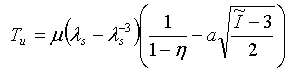
- 体積: p = pressure = -0.5K(J-1/J) where J = λ v 3 where
- 等軸:
![]()
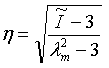
- Yeoh:
- 等軸: where I 1 =λ u 2 + 2λu -1
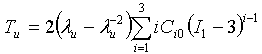
- 等二軸: where I 1 = 2λ B 2 + λB -4
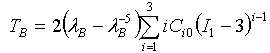
- 純せん断: where I 1 =λ S 2 + 1 + λ S -2
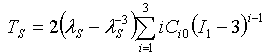
- 体積: where J = λ v 3
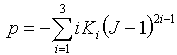
- 等軸:
[カーブフィットの入力データを比較]セクション
このセクションには、表形式のテスト データと近似曲線が示されます。[表示されたデータのタイプ]ドロップダウンを使用すると、グラフに表示するデータを選択できます。データが入力されているタイプであれば、そのデータがカーブ フィットで使用されているかどうかにかかわらず表示できます。(カーブ フィット ルーチンで使用されていないデータには、データに十分にフィットしない定数が含まれていることが多くあります。このため、近似曲線は表形式のデータに沿わない可能性が高いです。)
材料モデル定数を手動で変更すると、グラフは自動更新されません。 グラフを更新するには、[表示されたデータのタイプ]で再選択します。
カーブ フィットの例
Ogden 材料モデルでの単純引張、等二軸、および純せん断のテスト データを使用した例について検討してみましょう。
- ブリックまたは 2D 要素を伴うモデルを非線形の解析タイプに設定します(非線形材料による静解析または非非線形材料による MES 解析)。テスト データは MPa で与えられるため、モデル単位はニュートンおよびミリメートルとする必要があります。(1 MPa = 1 N/mm^2)
- 要素定義を編集します。パーツの[要素定義]を右クリックして、[要素定義を編集]を選択します。 [材料モデル]を[超弾性: Ogden]に設定します。 [OK]をクリックします。
- 材料特性を編集します。パーツの[材料]を右クリックして、[材料を編集]を選択します。 [カスタム]を選択して、[プロパティを編集]ボタンをクリックします。Ogden 材料モデルの定数が不明な場合は、直接入力することができます。材料テスト データ(以下)が得られたため、[カーブフィット]ボタンをクリックします。
- 単純引張り応力-ひずみテスト データを入力するには、[単純引っ張り]ボタンをクリックします。 スプレッドシートに行を追加して以下のデータを入力するか、以下のテキストを(拡張子が .CSV の)テキスト ファイルにコピー&ペーストして、[インポート]を使用してデータに読み込みます。完了したら[OK]をクリックします。
- 同様の方法で、等二軸応力-ひずみテスト データを入力します。[等二軸]ボタンをクリックします。スプレッドシートに行を追加して以下のデータを入力するか、以下のテキストを(拡張子が .CSV の)テキスト ファイルにコピー&ペーストして、[インポート]を使用してデータに読み込みます。完了したら[OK]をクリックします。
- 同様の方法で、純せん断応力-ひずみテスト データを入力します。[純剪断]ボタンをクリックします。スプレッドシートに行を追加して以下のデータを入力するか、以下のテキストを(拡張子が .CSV の)テキスト ファイルにコピー&ペーストして、[インポート]を使用してデータに読み込みます。完了したら[OK]をクリックします。
- [コントロール]タブで、テスト データそれぞれについてチェック ボックスをアクティブにします。
- Ogden 材料モデルの場合、パラメータのうち 1 つのみに関する見積もり値(α値)が要求される[部分的な線形最小二乗法]の[カーブフィット法]が手始めとして適切でしょう。 プルダウンからこの方法を選択します。その他の設定は既定のままにします。[体積弾性率オーダ]は、体積データが入力されていないため灰色表示となっていることに注意してください。
- [パラメータ]タブで、[Alphaの推定値]、[範囲値]、および[増分]を次のとおり設定します。このようにすることで、使用する解に対して適度に広範な値が与えられます。増分 20 はおおよその値となりますが、すべての順列を計算するのにそれほど時間を取らないため、初回実行時には適切な近似値となります。推定値は Ogden 材料モデルの既定値であることに注意してください。
オーダ
Alpha の推定値
範囲値
増分
1 1.2 10 20 2 -2 10 20 3 6 10 20 - [コントロール]タブで、[カーブフィットを実行]ボタンをクリックしてから[フィット]ボタンをクリックします。二乗平均平方根エラーは 0.184 で、最大応力に比べて相対的に大きくなります。[完了]ボタンをクリックします。
- [表示されたデータのタイプ]プルダウンを使用して、各カーブ フィット データ(単純引張、等二軸、および純せん断)のグラフを確認します。各曲線はテスト データに十分適切に沿っています(等二軸が最も逸れます)。このため、見つかる定数は正しい大きさ順になります。
- 適切な見積もり値を把握したところで、[カーブフィット法]を[Levenberg-Marquardtアルゴリズム]に切り替えます。その推定値を、以前に見つけられた解を使用して、[パラメータ]タブに入力します。見積もり値は正確でなくてもよいため、次のような概数値で十分です。
オーダ
Mu の推定値
Alpha の推定値
1 -0.16 6.2 2 4.4 0.5 3 0.026 9 - [コントロール]タブで、[カーブフィットを実行]ボタンをクリックしてから[フィット]ボタンをクリックします。二乗平均平方根エラーは 0.183 で、前回のフィットより良好になることはほとんどありません。しかし、この解法が部分的な線形最小二乗法よりいかに速いかに着目してください。
- 異なる初期値で追加の試行を行い、別の最小値を見つけることもできますが、より高いオーダ モデルを試行することの方が生産的であると考えられます。[コントロール]タブで、[モデルの順序]を 5 番目に、カーブ フィッティング法を[部分的な線形最小二乗法]に設定します。 [パラメータ]タブで、推定値を次のとおり入力します。 2 つの注意点があります。第一に、モデルのオーダが変更されたため、前回の解で見つけられた定数は、Levenberg-Marquardt のようなより効率的な解法アルゴリズムにおいて一般的には関連性のない推定値となります。この場合、部分的な線形最小二乗法でやり直すことをお勧めします。第二に、増分値が以前よりも下げられたことに注意してください。計算では、最初のオーダαのすべての組み合わせが、2 番目のオーダαのすべての組み合わせで行われ、このように進んでいくため、5 番目のオーダの解で多くの計算を早く作成することができます!より小さい増分値は、カーブ フィッティング ルーチンに掛かる時間を最小限に抑えるために使用されます。
オーダ
Alpha の推定値
範囲値
増分
1 1.2 10 10 2 -2 10 10 3 6 10 10 4 19 10 10 5 1 10 10 - [コントロール]タブで、[カーブフィットを実行]ボタンをクリックしてから[フィット]ボタンをクリックします。二乗平均平方根エラーは 0.142 です。予想されたとおり、[表示されたデータのタイプ]下のそれぞれの曲線は、テスト データによりフィットします。結果を図 1 に示します。追加の試行を行うことができますが、テスト データの精度を考慮すると、このカーブ フィットを許容可能とするべきです。
単純引張のテスト データ
0,0
0.02,0.08
0.06,0.12
0.28,0.30
0.47,0.4
0.67,0.57
0.77,0.7
0.82,0.78
0.85, 0.9
0.89, 1.0
等二軸のテスト データ
0,0
0.02,0.14
0.06,0.25
0.12,0.4
0.28,0.6
0.43,0.8
0.57,0.95
0.65,1.16
0.72,1.4
0.80,1.72
0.89,2.4
純せん断のテスト データ
0,0
0.02,0.08
0.07,0.2
0.20,0.37
0.59,0.71
0.73,0.92
0.83,1.1
0.89,1.28
 値
値