フォン ミーゼス材料モデルは、2D 要素、ビーム要素、シェル要素、ブリック要素、および 4 面体要素で使用できます。フォン ミーゼス材料モデルを使用するのは、弾性材料に材料の降伏強度を超える荷重がかかる場合です。その場合、塑性変形が発生します。フォン ミーゼス材料モデルと硬化材料モデルでは、応力値の計算に双線形曲線を使用します。応力とひずみの弾性域には、ヤング率に等しい勾配があります。応力とひずみの塑性域には、ひずみ硬化係数に等しい勾配があります。
硬化材料モデルには 2 つのタイプがあります。等方硬化モデルは、降伏曲面全体の均一な発生が伴います。移動硬化モデルは、(主に荷重の反転による)降伏曲面の移動が伴います。図 1 および 2 を参照してください。移動硬化モデルは、周期荷重(Bauschinger 効果)に関連する解析に適しています。ただし、実際の材料の応力-ひずみ挙動に基づいて、等方硬化モデルを使用するか移動硬化モデルを使用するかを決定する必要があります。
|
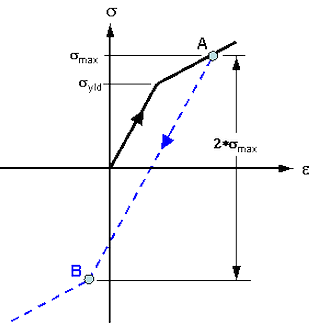
単軸応力-ひずみ曲線降伏応力を超えると、パーツは塑性的に変形し始めます。最大応力(点 A)に到達して荷重が除荷されると、破線に沿って荷重が低下します。パーツに再び荷重がかかっても、応力が点 A に到達するまで塑性変形は発生しません。 圧縮が開始されると、パーツは点 B に到達するまで破線に沿って弾性的に圧縮され、最終的に圧縮により降伏します。 等方硬化の場合、点 A から点 B までの応力の変化は最大応力の 2 倍になります。 |
|
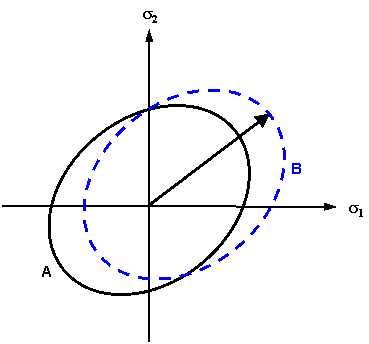
二軸応力-ひずみ曲線。二軸の場合、初期降伏曲面(曲面 A)内における応力の任意の組み合わせが弾性域にあります。初期降伏曲面を超えると、パーツに塑性変形が発生します。 等方硬化の場合、降伏曲面の中心は一定のままですが、曲面のサイズが増加します。新しい降伏曲面(曲面 B)内の応力状態で塑性変形が発生します。つまり、応力状態が曲面 B に到達すると、塑性変形が発生します。 |
| 図 1: 等方硬化 |
|
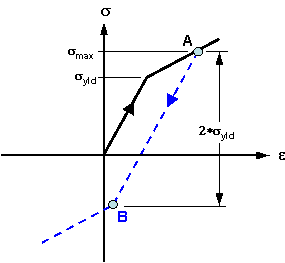
単軸応力-ひずみ曲線降伏応力を超えると、パーツは塑性的に変形し始めます。最大応力(点 A)に到達して荷重が除荷されると、破線に沿って荷重が低下します。パーツに再び荷重がかかっても、応力が点 A に到達するまで塑性変形は発生しません。 圧縮が開始されると、パーツは点 B に到達するまで破線に沿って弾性的に圧縮され、最終的に圧縮により降伏します。 移動硬化の場合、点 A から点 B までの応力の変化は降伏応力の 2 倍になります。 |
|
二軸応力-ひずみ曲線。二軸の場合、初期降伏曲面(曲面 A)内における応力の任意の組み合わせが弾性域にあります。初期降伏曲面を超えると、パーツに塑性変形が発生します。 移動硬化の場合、降伏曲面の中心が移動します。ただし、曲面のサイズは一定のままです。新しい降伏曲面(曲面 B)内の応力状態で塑性変形が発生します。つまり、応力状態が曲面 B に到達すると、塑性変形が発生します。 |
| 図 2: 移動硬化 |
フォン ミーゼス材料特性を次に示します。フォン ミーゼス材料特性はどちらのモデルでも同じです。また、一部の等方性材料特性の定義が必要になる場合もあります。
[降伏強さ]
材料の降伏強度は、材料で最初に塑性変形が発生する応力-ひずみ曲線上の点です。降伏の発生後、新しい降伏応力は硬化のタイプおよび荷重履歴によって決まります。
[ひずみ硬化係数]
ひずみ硬化係数は、材料の降伏点に到達した後における応力-ひずみ曲線の勾配です。
パーツの材料特性を材料ライブラリからロードする場合、ひずみ硬化係数は、双線形応力-ひずみ曲線を定義する 3 つの点を基準にします。つまり、(0,0)、降伏点、およびライブラリ マネージャで極限強度および 2 インチにおける離隔として特定されている 3 番目の点です。ひずみ硬化係数は次のように計算されます。
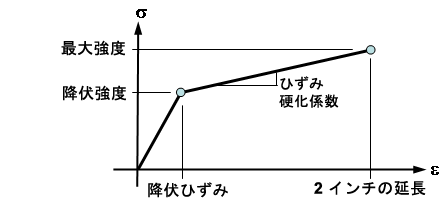
ひずみ硬化係数 = [極限強度 - 降伏強度]/[(2 インチにおける離隔)/100 - 降伏ひずみ]
ここで、降伏ひずみは降伏強度に対応するひずみです。つまり、「降伏ひずみ = (降伏強度) / (ヤング率)」となります。極限強度、降伏強度、2 インチにおける離隔、およびヤング率は材料ライブラリに格納されています。
構造の不安定性
フォン ミーゼス材料モデルを使用した場合、材料の降伏強度を超過すると、構造の剛性が低下して、構造が不安定になります。この状態では、弾性範囲内にある場合に比べて、構造の適用荷重への耐荷重特性は大幅に低下します。この不安定性は、数値解の収束困難、不安定または一貫性のない応力結果などとして現れます。このような状況では、次のモデル設定の調整が効果的です。
- 力の荷重を強制変位に変更します。
- イベントを解析するのに、複数の時間間隔を使用し、不安定な期間には小さい時間ステップ サイズを使用します。
- 座屈後の現象を取り込む目的で、Riks 座屈解析を実行してみます。追加の詳細については、次の 2 つのヘルプ トピックを参照してください。
- 「MES - 非線形構造解析」ページ内の Riks 座屈解析に関する内容
- 「Riks - 座屈後」ページの「解析パラメータ」