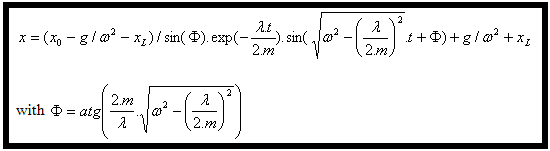Jedną z czynności w procesie odpowiedzialnego projektowania jest sprawdzanie. Aby sprawdzić projekt, często warto użyć prostych i niezawodnych przypadków teoretycznych. Przypadki takie opisano poniżej.
Przypadki te opisują równania i założenia wykorzystywane podczas sprawdzania danych wyjściowych symulacji.
Przemieszczenie, przypadek obciążnik-sprężyna
Prosty przypadek sprawdzenia układu obciążnik-sprężyna.

Prawo Newtona:
![]() (1)
(1)
Z:
| Wartość numeryczna: | |
|---|---|
| |
|
| |
|
| |
|
| |
10 |
| |
20 |
| |
15000 |
| |
0.3 |
| |
9.81 |
| |
0.33 |
| |
0.0 |
|
(1) |
|
|
z |
|
|
|
|
|
Rozwiązanie tego równania różniczkowego jest następujące: |
|
|
|
|
|
Rozwiązanie szczególne, gdy układ jest ustabilizowany, jest dla |
|
|
Następnie (2) |
|
|
|
|
|
|
|
|
Warunki początkowe określają wartość A i |
|
|
dla t = 0,0, (3) |
|
|
|
|
|
i |
|
|
|
|
|
Ostatecznie (4) i (6) podane w (3) dają równanie przemieszczenia: |
|
|
|
|
|
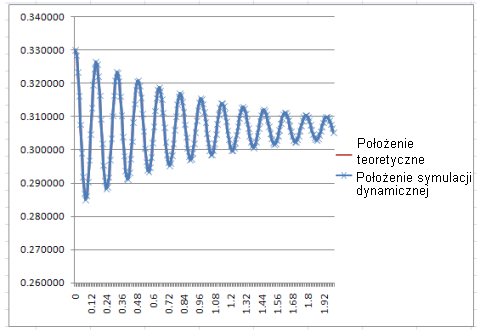
To równanie zostało następnie zaprogramowane w programie Excel i wyniki zostały porównane z wynikami otrzymanymi w symulacji dynamicznej i okazały się identyczne. |
|
 |
|
Położenie i prędkość, przypadek korba-tłok
Celem tego przypadku sprawdzenia jest sprawdzenie położenia i prędkości w wale korbowym oraz mechanizmie tłoka, gdy dane wyjściowe symulacji dynamicznej w porównaniu z równaniami teoretycznymi są takie same.
Znane wartości: „Rzut” lub odległość czopu wału korbowego od środka obrotu wału oraz długość pręta łączącego pomiędzy głównym czopem łożyska i złączem sworzniowym tłoka.
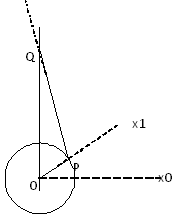
Diagram
|
Definicja |
R = długość(OP) = rzut wału korbowego L = długość(PQ) = długość pręta łączącego |
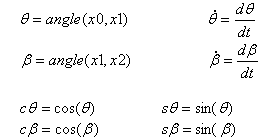 |
|
|
Prędkość punktu Q względem bezwzględnego układu współrzędnych R0 = (x0, y0) |
|
|
|
// położenie punktu Q w układzie R0 |
|
|
//prędkość punktu Q w układzie R0 |
| z:
|
|
| i:
|
|
|
|
|
| z: |
|
| i: |
|
| następnie: |
|
|
Punkt Q pozostaje na osi y0 a komponent x0 wynosi 0,0 : |
|
|
|
|
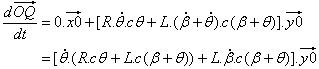 |
|
| Ostatecznie, używając (1): | |
|
|
|
|
Równanie (1) daje wartość |
|
|
(1) |
|
i 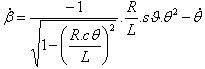 |
|
| Używając programu MS Excel i wartości numerycznych (L=0,125 m, R=0,06 m i |
|
|
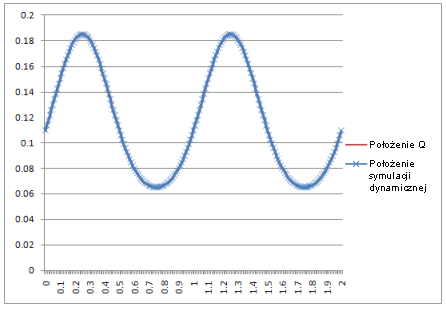
Położenie: |
|
 |
|
|
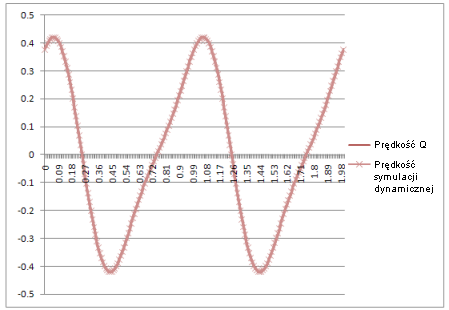
Prędkość: |
|
 |
|
Wynik: krzywe w symulacji dynamicznej są identyczne z krzywymi otrzymanymi na podstawie równań teoretycznych.
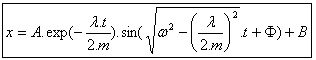 (3)
(3)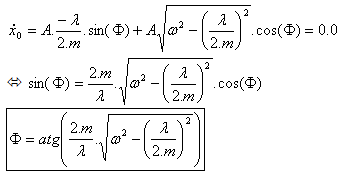 (5)
(5)