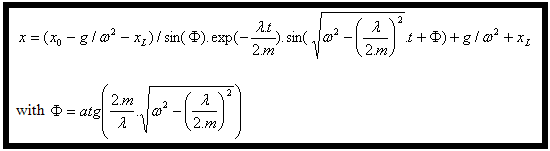Um dos passos responsáveis no processo de projeto é a validação. Para validar um projeto, costuma ser melhor utilizar casos teóricos confiáveis para estabelecer comparações. A seguir detalhamos estes casos.
Estes casos descrevem as equações e suposições utilizadas para conseguir validar os resultados de uma simulação.
Deslocamento, Caso da massa da mola
Um caso simples de validação de massa e mola.

Lei de Newton:
![]() (1)
(1)
Com:
| Valor numérico: | |
|---|---|
| |
|
| |
|
| |
|
| |
10 |
| |
20 |
| |
15000 |
| |
0,3 |
| |
9,81 |
| |
0,33 |
| |
0,0 |
|
(1) |
|
|
com |
|
|
|
|
|
Uma solução para esta equação diferencial é: |
|
|
|
|
|
Uma solução específica, quando o sistema está estabilizado, é para |
|
|
Seguidamente (2) |
|
|
|
|
|
|
|
|
As condições iniciais fornecem o valor de A e |
|
|
para t = 0,0, (3) |
|
|
|
|
|
e |
|
|
|
|
|
Por último, (4) e (6) registrados em (3) fornecem a equação do deslocamento: |
|
|
|
|
|
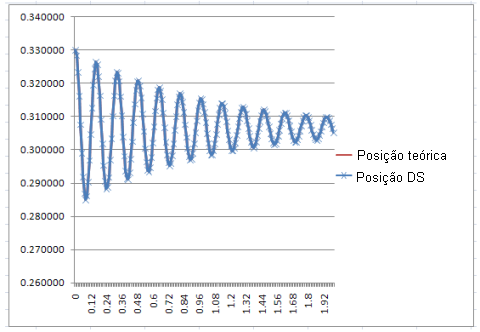
Esta equação foi então programada em Excel e os resultados comparados com os produzidos por simulação dinâmica, sendo estes resultados idênticos. |
|
 |
|
Posição e velocidade, o caso do pistão do motor
A finalidade deste caso de validação é verificar a posição e a velocidade de um mecanismo de eixo do motor e de pistão quando os resultados obtidos na simulação dinâmica, em comparação com as equações teóricas descrevem a mesma coisa.
Valores conhecidos: o “impulso” ou a distância do pino de articulação do eixo do motor desde seu centro de giro e o comprimento da barra de conexão entre o pino de articulação principal e a junta de pino do pistão.
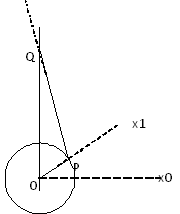
Diagrama
|
Definição |
R = comprimento (OP) = impulso do eixo do motor L = comprimento (PQ) = comprimento da barra de conexão |
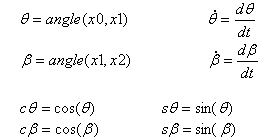 |
|
|
Velocidade do ponto Q em relação ao sistema de coordenadas absoluto R0 = (x0, y0) |
|
|
|
// posição de Q em R0 |
|
|
// velocidade de Q em R0 |
| com:
|
|
| e:
|
|
|
|
|
| com: |
|
| e; |
|
| então: |
|
|
O ponto Q permanece no eixo y0 e o componente x0 é 0,0 : |
|
|
|
|
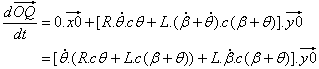 |
|
| Por último, utilizando (1): | |
|
|
|
|
A equação (1) fornece |
|
|
(1) |
|
e 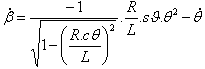 |
|
| Com MS Excel e valores numéricos (L=0,125 m, R=0,06 m e |
|
|
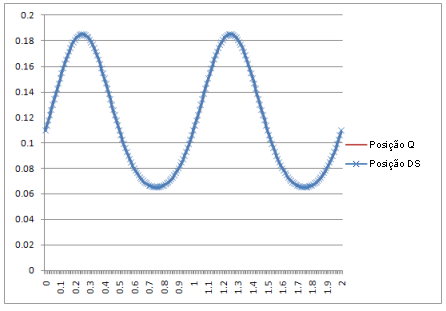
Posição: |
|
 |
|
|
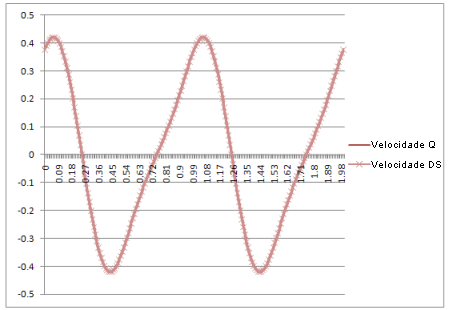
Velocidade: |
|
 |
|
O resultado: as curvas na simulação dinâmica são idênticas às produzidas pelas equações teóricas.
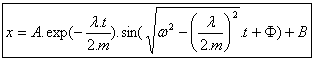 (3)
(3)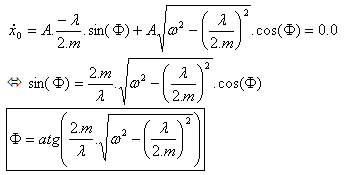 (5)
(5)