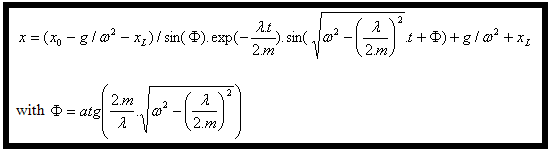Одним из этапов процесса проектирования является проверка. Чтобы проверить проект, рекомендуется провести анализ по приведенным ниже теоретическим аспектам.
Они представлены в виде уравнений и допущений, используемых для оценки правильности результатов моделирования.
Система масс и пружины: смещение
Простой случай оценки системы масс и пружины.

Закон Ньютона:
![]() (1)
(1)
Где:
| Численное значение: | |
|---|---|
| |
|
| |
|
| |
|
| |
10 |
| |
20 |
| |
15000 |
| |
0,3 |
| |
9,81 |
| |
0,33 |
| |
0,0 |
|
(1) |
|
|
На |
|
|
|
|
|
Решение данного дифференциального уравнения: |
|
|
|
|
|
Частное решение для стабильного состояния системы, когда |
|
|
Тогда (2) |
|
|
|
|
|
|
|
|
С учетом исходных условий значения A и |
|
|
для t = 0,0, (3) |
|
|
|
|
|
и |
|
|
|
|
|
Наконец, учитывая (4) и (6), используемые в (3), получаем следующее уравнение смещения: |
|
|
|
|
|
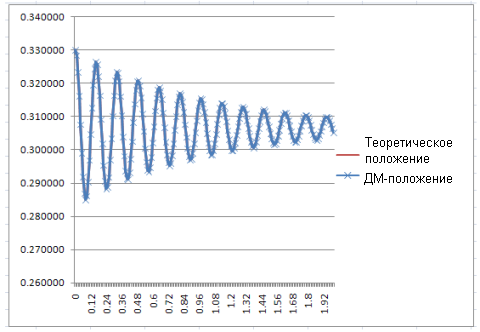
Затем данное уравнение было обработано с помощью Excel, а результаты сравнили с результатами, полученными при динамическом моделировании. Результаты оказались идентичными. |
|
 |
|
Кривошип и шатун: положение и скорость
Цель данной проверки состоит в оценке положения и скорости в кривошипно-шатунном механизме, когда результат динамического моделирования и теоретические уравнения описывают один случай.
Известные значения: “Ход” или расстояние от центра вращения коленчатого вала до шейки вала и длина шатуна между шейкой под подшипник и соединением поршневого пальца.
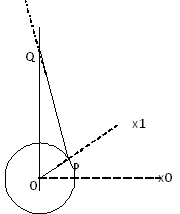
Диаграмма
|
Определение |
R = длина (OP) = ход коленчатого вала L = длина (PQ) = длина шатуна |
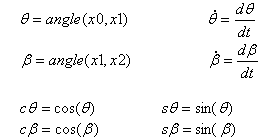 |
|
|
Скорость точки Q в абсолютной системе координат R0 = (x0, y0) |
|
|
|
// положение Q в R0 |
|
|
//скорость Q в R0 |
| где:
|
|
| и
|
|
|
|
|
| где: |
|
| и |
|
| тогда: |
|
|
Точка Q остается на оси y0, и ее координата по оси x0 равна 0,0: |
|
|
|
|
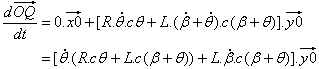 |
|
| Наконец, используя (1): | |
|
|
|
|
Получаем уравнение (1), где |
|
|
(1) |
|
и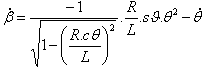 |
|
| С помощью программы Excel, используя численные значения (L = 0,125 м, R = 0,06 м и |
|
|
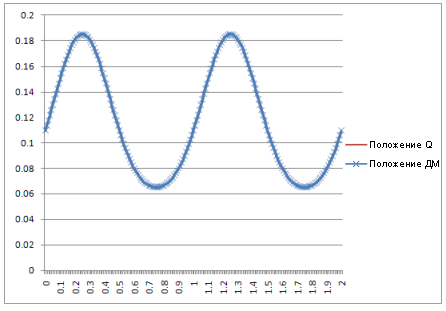
Положение: |
|
 |
|
|
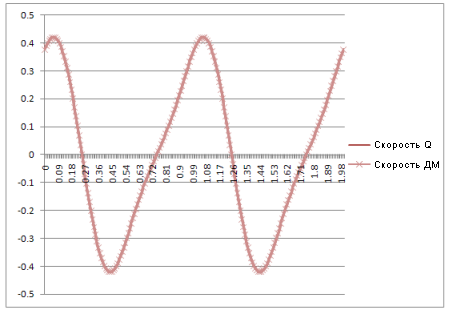
Скорость: |
|
 |
|
Результат: кривые, полученные при динамическом моделировании, идентичны кривым, рассчитанным с помощью теоретических уравнений.
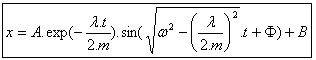 (3)
(3)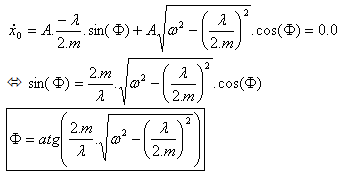 (5)
(5)