在土木工程中使用多种缓和曲线,以在切线和圆形曲线之间以及两条具有不同曲率的圆形曲线之间逐渐引入曲率和超高。
在与其他切线和曲线的关系中,每条缓和曲线要么为内曲,要么为外曲。
工程师在设计和布局缓和曲线时最常用的两个参数为 L(缓和曲线长度)和 R(圆形曲线的半径)。
下图显示了缓和曲线的各种参数:
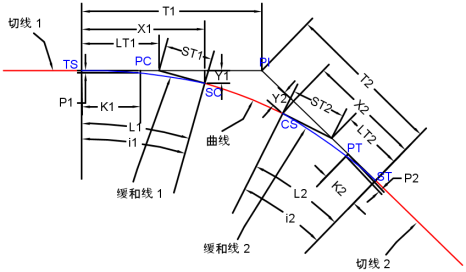
| 缓和曲线参数 | 描述 |
| i1 | 缓和曲线曲线 L1 的圆心角,此圆心角为螺旋角。 |
| i2 | 缓和曲线曲线 L2 的圆心角,此圆心角为螺旋角。 |
| T1 | 从交点到 TS 的总切线距离。 |
| T2 | 从交点到 ST 的总切线距离。 |
| X1 | SC 处自 TS 的切线距离。 |
| X2 | CS 处自 ST 的切线距离。 |
| Y1 | SC 处自 TS 的切线偏移距离。 |
| Y2 | CS 处自 ST 的切线偏移距离。 |
| P1 | 初始切线进入移动曲线的 PC 的偏移。 |
| P2 | 初始切线出来到移动曲线 PT 的偏移。 |
| K1 | 参照 TS 的移动 PC 的横坐标。 |
| K2 | 参照 ST 的移动 PT 的横坐标。 |
| LT1 | 长切线前缓和曲线。 |
| LT2 | 长切线后缓和曲线。 |
| ST1 | 短切线前缓和曲线。 |
| ST2 | 短切线后缓和曲线。 |
| 其他缓和曲线参数 | |
| A1 | A 值等于缓和曲线长度乘以半径的平方根。缓和曲线平面度的测量值。 |
| A2 | A 值等于缓和曲线长度乘以半径的平方根。缓和曲线平面度的测量值。 |
公式
复合缓和曲线
复合缓和曲线提供两条具有不同半径的圆形曲线之间的过渡。与简单缓和曲线一样,复合缓和曲线也考虑曲率函数的连续性,并提供在超高中引入平滑过渡的方法。
回旋线
尽管 AutoCAD Civil 3D 支持若干类型的缓和曲线,回旋线是最常用的缓和曲线类型。回旋线广泛用于公路和铁路铁轨设计。
由瑞士数学家 Leonard Euler 最先研究,回旋曲线的曲率函数是所选择的线性函数,从而缓和曲线与切线相交处的长度函数曲率为零 (0)。然后,曲率将线性增加直到其等于缓和曲线和曲线交点处相邻曲线的曲率。
此种路线提供了位置函数及其第一个衍生对象(局部方位角)的连续性,如同切线和缓和曲线在曲率点 (PC) 处所起的作用。但是,与简单曲线不同,它还保持第二个衍生对象(局部曲率)的连续性,这在速度较高时变得日益重要。
公式
回旋缓和曲线可以表示为:![]()
缓和曲线的平面度:![]()
由缓和曲线对向的总角度:![]()
从切线-缓和曲线点到缓和曲线-曲线点的切线距离为:
从切线-缓和曲线点到缓和曲线-曲线点的切线偏移距离为:
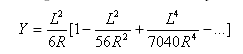
Bloss螺线
除了使用回旋曲线之外,带有五次抛物线的 Bloss 螺线也可用作过渡。此缓和曲线优于回旋曲线,因为移动 P 较小,从而会有较长的过渡以及较大的缓和曲线扩展 (K)。这是铁路设计中的一个重要因素。
公式
Bloss螺线可以表达为:
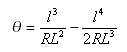
其他关键表达式:
从切线-缓和曲线点到缓和曲线-曲线点的切线距离为:
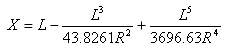
从切线-缓和曲线点到缓和曲线-曲线点的切线偏移距离为:
正弦曲线
这些曲线表示曲率的一致路线,并且适用于切线偏转 0 到 90 度之间的过渡。但是,由于正弦曲线比真实的缓和曲线更陡,而很难对其进行列表和放样,所以并未得到广泛使用。
公式
正弦曲线可以表示为:
求 | 的微分,可以获得一个 |/r 的方程式,其中 r 为任意给定点处曲率的半径。

正弦半波长递减正切曲线
此形式的方程式通常用于日本的铁路设计。此曲线在更改低偏转角度(关于车辆动力学方面)的曲率时需要有效过渡的情况下非常有用。
公式
正弦半波长递减正切曲线可以表达为:
其中 ![]() 和 x 是指从起点到曲线上任意点的距离,并且是沿(已扩展)初始切线测量得到的;X 是指缓和曲线末端的总距离 X。
和 x 是指从起点到曲线上任意点的距离,并且是沿(已扩展)初始切线测量得到的;X 是指缓和曲线末端的总距离 X。
其他关键表达式:
从切线-缓和曲线点到缓和曲线-曲线点的切线距离为:
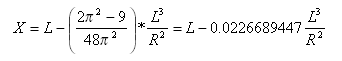
从切线-缓和曲线点到缓和曲线-曲线点的切线偏移距离为:
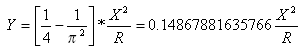
三次缓和曲线 (JP)
此缓和曲线是为满足日本的需要而开发的。还开发了某些近似回旋曲线,以便在需要适应较小的偏转角度或较大半径的情况下使用。其中一种近似回旋曲线(用于日本的设计)就是三次缓和曲线 (JP)。
公式
三次缓和曲线 (JP) 可以表达为:
其中 X = 缓和曲线-曲线点处自切线-缓和曲线点的切线距离
此公式还可以表达为:
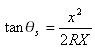
其中 ![]() 为圆心角缓和曲线(如插图 i1 和 i2 中所阐明)
为圆心角缓和曲线(如插图 i1 和 i2 中所阐明)
其他关键表达式:
从切线-缓和曲线点到缓和曲线-曲线点的切线距离为:
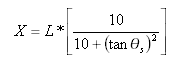
从切线-缓和曲线点到缓和曲线-曲线点的切线偏移距离为:
三次抛物线
三次抛物线的收敛速度比三次缓和曲线稍快,因而在铁路和公路设计领域中广泛使用。虽然它们不如三次缓和曲线准确,但由于三次抛物线是用笛卡尔坐标表示的,并且易于在现场测定,因此三次抛物线常用于公路和铁路工程领域。
公式
当 ![]() -> 零 -> 可以假设 cos
-> 零 -> 可以假设 cos![]() = 1,则 x = l。
= 1,则 x = l。
此外,如果假设 sin![]() =
= ![]() ,则
,则
x = l 且 TotalX = (近似)L
替换该近似值有助于获得以下方程式:
所有其他参数均与回旋缓和曲线相同。
三次抛物线的最小半径
三次抛物线上任意点的半径为:
三次抛物线在以下值处获得最小 r:
因此 ![]()
三次抛物线半径从无穷大减少到![]() 24 度,5 分,41 秒,然后又开始增加。这使得三次抛物线无法用于大于 24 度的偏转。
24 度,5 分,41 秒,然后又开始增加。这使得三次抛物线无法用于大于 24 度的偏转。
四次 (Schramm) 缓和曲线
四次 (Schramm) 缓和曲线垂直加速度的值较小。它们包含两条二次抛物线,其中半径作为曲线长度的函数而变化。
简单曲线公式
第一条抛物线的曲率:
![]() 其中
其中 ![]()
第二条抛物线的曲率:
![]() 其中
其中 ![]()
根据缓和曲线用户定义的长度 (L) 指定该曲线。
复合曲线公式
第一条抛物线的曲率:
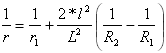 其中
其中 ![]()
第二条抛物线的曲率:
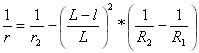 其中
其中 ![]()