在使用长纤维复合材料执行纤维取向分析已实现后，用来计算纤维翘曲的选项。
所实现的纤维翘曲模型首先由 Phelps 和 Tucker [1] 作为一种统计模型提出，用来描述由于流动场中的挫曲和剪切力而导致纤维断开的概率。
对于单个纤维，在液体动力下断开的概率可表示为：
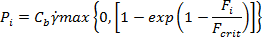
其中，力比是液体动力压缩力（根据 Dinh 和 Armstrong [2] 的描述）与重要的挫曲力的比值，例如：
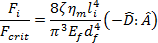
其中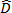 
和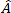 
分别是变形速率张量和纤维取向张量。除了作为曳力因子的 
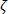以外，其他变量都是纤维和基体的属性。
由于纤维不能消失，也不能在流动场中生长，所以无论断开与否，都必须遵守守恒定律。此守恒定律可表示为：
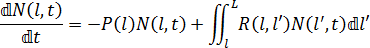
其中 L 是初始纤维长度，N(l,t) 是在时间 t 时长度为 l 的纤维数量，P(l) 是纤维长度 l 的标量概率函数，R(l,l') 是断开以形成纤维长度 l' 的纤维长度 l 的概率函数（其中 l'它可以表示为高斯翘曲曲线，例如：
其中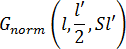 
是变量 L（具有平均值 l'/2 和标准偏差 Sl'）的高斯正态概率密度函数。S 是无量纲调整参数，可用来控制高斯翘曲曲线的形状。
参考
- Phelps, J.H., Processing-microstructure Models for Short- and Long-fiber Thermoplastic Composites. Ph.D. thesis, University of Illinois at Urbana-Champaign (2009).
- Dinh, S.M. and Armstrong, R.C., A Rheological Equation of State for Semi-Concentrated Fiber Suspensions. J. Rheol., 28(3):207-227 (1984).