选择哪种最合适的分析技术取决于零件几何。薄壳状的零件应使用“双层面”分析,而局部区域较厚的零件则最好使用 3D 分析技术进行分析。
厚度是横截面的最小尺寸。作为壳状特征,厚度应不大于横截面较大尺寸(例如宽度)的 4 倍。零件中大部分为壳状特征时,双层面模型最适用。3D 模型精确表示厚度未予以明确定义的零件。
因此,厚度计算会因所使用的分析类型而不同。基于上述原因,不管是针对双层面模型还是 3D 模型计算厚度,厚度结果都会不同。
对于双层面零件,厚度对应于零件两侧面之间的距离。因此,厚度在具有恒定壁厚的壳状零件中是均匀的。双层面模型是表示壳状零件的最佳选择。(参见图 1)
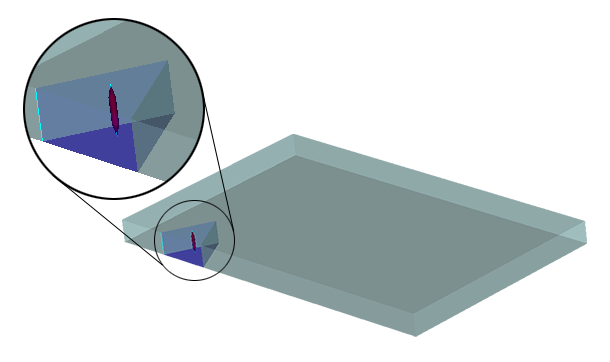
对双层面模型的厚度计算
但是,对于 3D 零件,厚度不明显,很难从外观上确定。要计算 3D 零件上的厚度变化,需使用最大球算法。
最大球算法认为在零件内部滚动的球需要变得更小一些方可到达边缘(参见图 2)。较大的红球与零件的顶面和底面接触,几乎接触到侧壁。较小的黄球与顶壁和一个侧壁接触,表示球接近拐角时距离较小。因此,厚度显示为由较小球在拐角处计算所得的较小值。如果将 3D 模型用于具有“均匀”壁厚的壳状零件,则 3D 模型会将零件的拐角显示的更薄些。最大球技术显示拐角的 3D 特性。

对 3D 模型的厚度计算
此方法最适用于 3D 零件,因为它可显示更真实的结果。零件的薄区域所需的冷却时间短,但流阻较大。零件的厚区域所需的冷却时间长,但流阻较小。