您可以选择以下一个或多个结果：
- 主残余应力（第一主应力和第二主应力）。
- 最大剪切应力。
- Mises-Hencky 应力。
这些结果的数学推导可由描述一个点处应力状态的著名的莫尔圆辅助说明。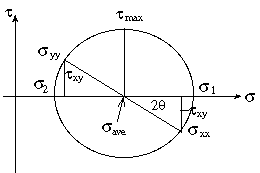
第一主应力和第二主应力
主应力是法线应力的极值。因为主应力表征一个点处的应力的物理状态，它们可独立于任何坐标参考。主应力使用以下方法进行计算：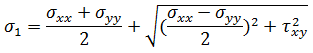 
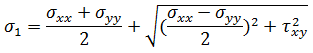
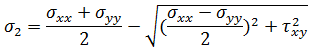
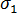为最大法线应力， 
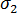为最小法线应力。主应力的相应方向分别称为第一主方向和第二主方向。第一主方向和第二主方向的角度使用以下公式进行计算：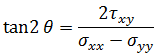 
注： 主应力值为正表示张力，而主应力值为负则表示压力。
最大剪切应力
最大剪切应力是剪切应力的极值，计算公式如下： 
Mises-Hencky 应力
Mises-Hencky 应力的计算公式如下：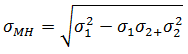 
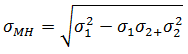
注： 可从以上公式看出，Mises-Hencky 应力值始终为正。由于从单元质心到单元边采用外推法，Mises-Hencky 应力可能生成很小的负值。这些很小的负值应当视为等于零。
解释应力结果
通常，检查应力结果时，应该检查零件内的应力分布和零件中的最大应力等级以及单元顶部和底部的应力和翘曲输出结果（归一化厚度分别为 1 和 -1）。
需要将这些同材料的推荐最大应力和零件的任何相关设计条件（例如，指定的失败条件）进行比较。
非填充的各向同性材料通常将呈现出易碎行为或柔软行为，如下图所示，其中 (a) 表示易碎行为，(b) 表示柔软应力-应变行为。
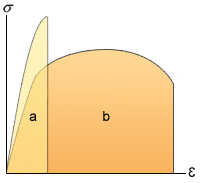
每种情况下应该考虑的推荐应力结果包括：
- 对于易碎材料，需要考虑主应力结果。
- 对于柔软材料，应该考虑 Mises-Hencky 结果。
对于纤维填充的各向异性材料，其负载下的零件行为、机械故障以及失败设计条件都比各向同性材料复杂得多。复合材料的应力分析和获得结果的解释需要用户具有零件的专业知识。
纤维取向和应力/翘曲分析在整个零件厚度的每个层基础上输出结果。
注： 主应力取向可能不对应于主纤维取向。应力取向数据取决于应力状态，位于每层的中心。纤维取向数据在层接口处进行计算，是一种材料属性。