冷却是真正的 3D 模具冷却分析产品。它使用由 BEM(边界元法)发展而来的数值方法。从物理角度来说,BEM 在求解过程中将所有边界作为热源(获得/损失热)。
模具中的温度是由合并所有源的影响而确定的。
3D 模具的平衡温度场可通过拉普拉斯方程表示为: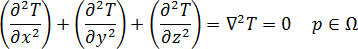
其中: 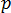 ,边界条件统一为:
,边界条件统一为:
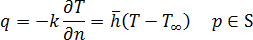
 为温度
为温度 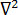 为拉普拉斯运算符
为拉普拉斯运算符 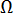 表示模具的表面区域和内部
表示模具的表面区域和内部
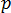 ,边界条件统一为:
,边界条件统一为: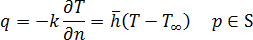
其中:
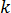 为模具材料的热传导率
为模具材料的热传导率 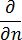 表示模具边界上朝外的法向衍生,
表示模具边界上朝外的法向衍生, 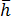 是模具边界上的等效热传到系数,
是模具边界上的等效热传到系数, 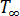 是周围环境的等效温度,
是周围环境的等效温度, 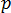 表示一个特定的点,
表示一个特定的点, 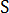 为模具表面(边界)
为模具表面(边界)
若要了解 BEM 如何将所有边界条件应用到模具温度场的解,让我们从加权残值表达式开始: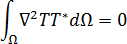
其中,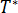 是权重函数。
是权重函数。
通过利用格林第二恒等式,等式 3 可转化为以下形式: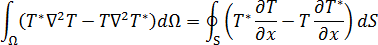
选择 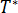 因为等式 1 的基本解定义如下:
因为等式 1 的基本解定义如下: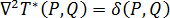
其中,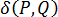 为狄拉克 δ 函数。对于 3D 模具,此函数可以表示为:
为狄拉克 δ 函数。对于 3D 模具,此函数可以表示为: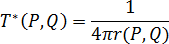
其中:
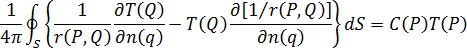
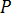 和
和 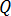 是空间中的两个点,
是空间中的两个点, 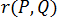 表示两点之间的距离,
表示两点之间的距离,
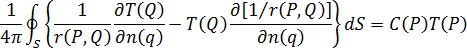
其中:
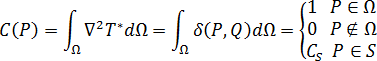 和
和 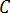 是与实体内角成比例的常量。
是与实体内角成比例的常量。
现在,等式 7 仅具有边界集成。所以,如果将所有模具表面 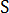 划分成
划分成 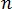 个单元,并且假定温度和温度梯度在每个边界单元上恒定,则等式 7 可离散化为以下形式:
个单元,并且假定温度和温度梯度在每个边界单元上恒定,则等式 7 可离散化为以下形式:
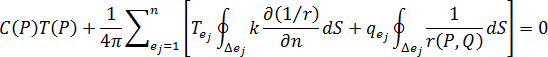
。其中,
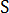 划分成
划分成 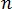 个单元,并且假定温度和温度梯度在每个边界单元上恒定,则等式 7 可离散化为以下形式:
个单元,并且假定温度和温度梯度在每个边界单元上恒定,则等式 7 可离散化为以下形式: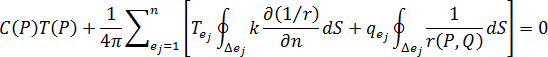
。其中,
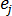 为一个特定单元
为一个特定单元 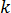 为模具材料的热传导率
为模具材料的热传导率 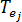 是单元
是单元 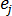 的温度
的温度
温度影响条件(所谓的 H 条件)表示单元 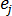 上 到点
上 到点 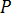 处的温度影响强度,具体由此表达式给出:
处的温度影响强度,具体由此表达式给出: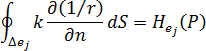
热通量影响条件(或所谓的 G 条件)表示单元 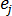 上 到点
上 到点 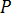 处的热通量输入影响强度,具体由此表达式给出:
处的热通量输入影响强度,具体由此表达式给出: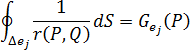
假设 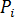 是
是 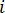 单元的质心。如果我们将等式 9 中的
单元的质心。如果我们将等式 9 中的 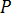 替换为
替换为 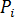 ,我们将获得如下所示的
,我们将获得如下所示的 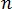 线性方程式:
线性方程式: