在使用热塑性、半结晶材料且相应的结晶形态属性数据已实现后，用来执行结晶分析的选项。
结晶固化动力学建模
结晶固化动力学建模，包括流动增强的结晶以及在剪切流动过程中及之后因流动而产生的半结晶材料形态变化，均已在热塑性塑料流动求解器中实现。
未发现晶体生长率受到材料流动的显著影响。因此，假设生长率仅取决于温度并遵守 Hoffman-Lauritzen 理论[1]： 
其中 
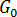和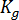
是与材料等级相关的常量，由静态条件决定， 
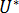是运动的激活能量， 
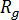是气体常量， 
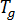是玻璃转变温度， 
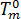是与材料等级相关的平衡熔化温度，假定其仅由压力决定。
线性函数[2]被选择用来描述压力相关性[2]：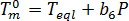 
其中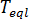 
是平衡熔化温度， 
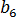是材料的 PVT 模型的与等级相关的常量， P 表示压力。
核代表示为静态条件下激活核数的总和，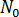 
，以及因流动引起的激活核数，
： 
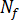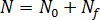
静态条件下激活核子的数量假定为是过冷却温度的唯一函数，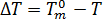 
，它是由 [3] 描述的： 
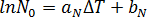其中 
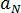和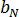 
是与材料等级相关的常量。
流动对结晶产生的影响通过将多余的自由能以及因流动产生的取向关联到结晶固化动力学来体现。流动产生的核数通过以下不同的方程给出：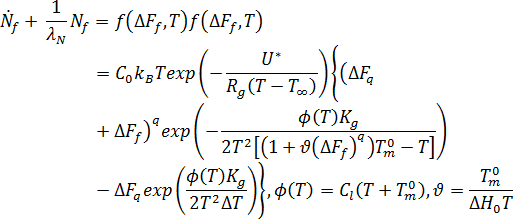 
结晶度的发展导致粘度的增加，最终发生凝固。在模拟中采用增强因子来描述粘度[4]对结晶度的影响： 
其中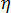 
是整个系统的粘度， 
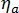是非结晶阶段的粘度， 
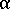是相对结晶度。
参考
[1] Lauritzen, S. I., and J. D. Hoffman, ''Theory of formation of polymer crystals with folded chains in dilute solution,'' J. Res. Natl. Bur. Stand. 64A，73-102 (1960)
[2] Fulchiron, R., E. Koscher, G. Poutot, D. Delaunay, and G. Regnier, ''Analysis of the pressure effect on the crystallization kinetics: dilatometric measurements and thermal gradient modelling,'' J. Macromol. Sci., Phys. 40, 297-314 (2001)
[3] Koschei, E., and R. Fulchiron, ''Influence of shear on polypropylene crystallization: morphology development and kinetics,'' 聚合物 43, 6931-6942 (2002)
[4] Zheng, R. and P. K. Kennedy, "A model for post-flow induced crystallization: General equations and predictions", J. Rheol., 48(4), 823-842 (2004)