已在假設線性熱黏彈性材料行為的情況下,公式化殘留應力收縮預測模型。它會說明當模具中的材料在壓力下冷卻時產生的應力。透過此方法,而不是計算收縮應變,我們可以直接計算每個元素的殘留應力分佈。
殘留應力分佈提供了平行及垂直於流動的方向上,每個元素整個厚度中的應力。然後會將此應力分佈輸入至「應力」分析程式,進而取得零件的撓曲形狀。另外,如果材料可以使用實驗性收縮資料,那麼與使用殘留應變方法相比,此方法能夠更準確地預測收縮,並因此更準確地預測零件撓曲。
對方法的一般說明
已在假設線性熱黏彈性材料行為的情況下公式化模型。它會說明當模具中的材料在壓力下冷卻時產生的應力。此模型尤其會說明由熱所引發的應力 (由材料凝固與隨後的收縮所致) 與由壓力引發的應力。後一種應力的產生由對形成凝固層之凝固材料的熔膠施加壓力所致。根據理論,此模型有一個優點,那就是即使材料沒有可用的收縮資料,仍可以使用它。但若有可用的收縮資料,其效能便可得到顯著改善。
對收縮與翹曲的預測以計算的由熱與壓力所引發的殘留應力分佈為基礎。目前展開的計算程序如下所示。此程序適用於纖維充填的材料。針對未充填的材料,程序類似,但不需要計算機械性質。
針對每個時間步長:
- 計算流體力學:
- 壓力 P、流速 Q...
- 纖維配向
- 計算熱傳導:
- 溫度 T
- 凝固層
- 計算熱力學:
- f (p, v, T)=0
- 更新黏度。
- 是否要收斂解?
- 如果為「否」,請從「步驟 1」開始重複。
- 如果為「是」,請前往「步驟 6」。
- 計算微觀力學:
-
熱力學性質:
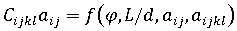
-
- 計算熱黏彈力學:
- 由熱與壓力所引發的應力
- 如果
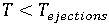 ,請前往下一個時間步長 (從步驟 1 開始重複)。
,請前往下一個時間步長 (從步驟 1 開始重複)。
注意:選取「殘留熱應力」收縮模型時,「翹曲」分析會使用非對稱「充填與保壓」分析產生的非對稱資訊。不對稱可能由模具兩側的溫差或/及支化的幾何圖形所致。因此,即使沒有「冷卻」分析結果,若零件擁有支化的幾何圖形,翹曲結果也可能會顯示一些非對稱影響。但是,如果「充填與保壓」分析對稱,則「翹曲」分析將會對稱,並因此忽略差異冷卻。
在沒有可用的收縮資料時應用此方法
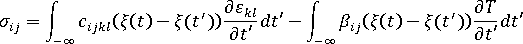
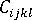 和
和 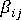 分別是定義材料的機械特性與熱特性的張量。
分別是定義材料的機械特性與熱特性的張量。 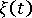 是說明材料溫度相依性的虛擬時間比例,並由以下方程式定義: 其中,
是說明材料溫度相依性的虛擬時間比例,並由以下方程式定義: 其中,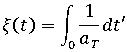
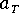 是時間-溫度變化係數,其特性由 WLF 方程式或 Arrhenius 方程式決定 (視材料與溫度範圍而定)。
是時間-溫度變化係數,其特性由 WLF 方程式或 Arrhenius 方程式決定 (視材料與溫度範圍而定)。
- 針對非纖維充填材料,模型為等向性,機械性質張量
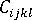 由材料 (當儲存於 Autodesk Simulation Moldflow 材料資料庫時) 的模數與蒲松氏比定義,且您可以從材料的 pvT 資料中取得用於定義熱性質張量
由材料 (當儲存於 Autodesk Simulation Moldflow 材料資料庫時) 的模數與蒲松氏比定義,且您可以從材料的 pvT 資料中取得用於定義熱性質張量 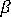 的熱膨脹係數。
的熱膨脹係數。 - 針對纖維充填材料,會使用從纖維配向分佈 (從「充填與保壓」分析取得) 計算所得複合材料的非等向性機械與熱性質,來定義這些張量。在此情況下,模型會預測沿纖維配向方向及橫向於纖維配向方向的應力。
- 在材料低於轉換溫度之前,材料中不會產生應力。
- 就 x3 方向正垂於局部中間平面的局部元素座標而言, 剪應力 =
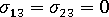 。
。 - 整個厚度上的法向應力
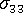 恆定。
恆定。 - 只要
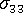 < 0,材料就會黏到模具壁上。
< 0,材料就會黏到模具壁上。 - 只要材料位於模具中,就會指定所有情況下的受約束抑制條件。
- 模具彈性會遭到忽略。(會在公模仁偏移分析中考慮模具公模仁彈性)。
- 頂出零件之後,材料會表現得像彈性實體一樣。
您可以在所有材料均位於 Autodesk Simulation Moldflow 材料資料庫中的情況下使用此模型,而不管其是否已接受收縮特性。若為纖維充填材料,模型要求在「製程設定精靈 - 充填與保壓設定」對話方塊中選取執行「對於纖維材料的情況進行纖維配向分析」的選項。
此模型可預測收縮趨勢,但對於得出的絕對值而言,可能會產生大量錯誤。這對於設計以減少翹曲來說很有用,但與可以使用收縮資料時相比,絕對值的準確性較低。針對未充填的材料,模型為等向性,因為沒有工具可計算流動分析軟體中分子配向或結晶性的影響。
在可以使用收縮資料時應用此方法
- 收縮對轉換溫度與 pvT 資料 (使用目前測量方法) 的相依性很敏感,無法表示實際射出成型條件下的行為。
- 沒有對決定分子配向的規定,因此針對未充填的材料,模型不會預測異向性。
- 沒有對結晶性影響的規定。
- 黏彈性計算無鬆弛光譜資料。
當 Autodesk Simulation Moldflow 已描繪材料的收縮特性時,說明測量的收縮結果可大大改進熱黏彈性模型。執行此操作的方法是將理論模型做為混合模型中的其中一個自變數使用,該混合模型會與測量的收縮資料關聯,以減少測量的與預測的收縮之間的差異。產生的模型稱為「修正的殘留模內應力」(CRIMS) 模型。
概念說明如下:
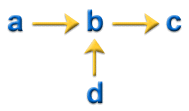
修正的殘留模內應力 (CRIMS) 模型
. (a) 預測的等向性殘留應力 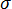 ,(b) 錯誤修正,(c) 修正的非等向性殘留應力
,(b) 錯誤修正,(c) 修正的非等向性殘留應力 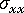 和
和 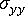 ,(d) 測量的收縮。
,(d) 測量的收縮。
若要說明其影響,請考慮下圖。
聚丙烯的平行收縮
. (a) 收縮百分比,(b) 設定的成型條件數,![]() 測量的平行位置,
測量的平行位置,![]() 修正的平行位置,
修正的平行位置,![]() 已計算臨界值 (等向性)。
已計算臨界值 (等向性)。
此圖顯示平行於聚丙烯流動方向的已測量實驗性收縮。也顯示了平行收縮理論上計算的值 (使用熱黏彈性模型) 與平行收縮的修正值。很明顯,修正的值與測量的值相當一致。下圖對相同聚丙烯垂直方向的相似改進狀況進行了說明。
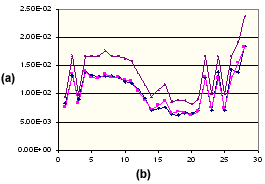
聚丙烯的垂直收縮
. (a) 收縮百分比,(b) 設定的成型條件數,![]() 測量的垂直位置,
測量的垂直位置,![]() 修正的垂直位置,
修正的垂直位置,![]() 已計算臨界值 (等向性)。
已計算臨界值 (等向性)。
修正的概念也可套用至纖維充填材料,它也會產生完美的結果。以下是玻璃纖維強化材料佔重量 15% 的 PA66 的某些結果。
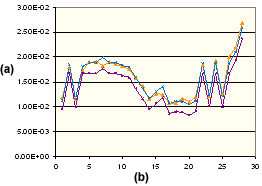
PA66 15% GF 的平行收縮
. (a) 收縮百分比,(b) 設定的成型條件數,![]() 測量的平行位置,
測量的平行位置,![]() 修正的平行位置,
修正的平行位置,![]() 理論上的平行位置。
理論上的平行位置。
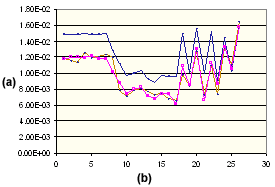
PA66 15% GF 的垂直收縮
. (a) 收縮百分比,(b) 設定的成型條件數,![]() 測量的垂直位置,
測量的垂直位置,![]() 理論上的垂直位置,
理論上的垂直位置,![]() 修正的垂直位置
修正的垂直位置
在與單一變量分析搭配使用時應用此方法
單一變量分析是 Autodesk Simulation Moldflow 翹曲分析產品中提供的一種技術,可隔離翹曲主因,並讓您採取針對性措施來減少零件翹曲。「單一變量分析」主題已對其做了詳細介紹。在此,我們將考慮如何在單一變量分析內容中套用殘留應力方法。
充填與保壓階段的「充填與保壓」分析會輸出做為殘留應力計算的輸入使用的以下資訊:
- 局部元素軸線系統中每個元素上的廣義力資料,即薄膜力 (
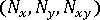 ) 與彎矩 (
) 與彎矩 (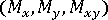 ),
), - 每個元素的材料配向角度,
- 每個元素的機械性質 (縱向楊氏模數、橫向楊氏模數與蒲松氏比)。
單一變量分析以翹曲原因的概念為基礎,這些原因可分為三個品類:
- 差異冷卻、
- 差異收縮、
- 配向性影響。
此概念與收縮 (而不是應力) 有關。因此,若要在使用殘留應力模型時,以上述三種影響的形式隔離翹曲原因,我們需要從指定的廣義力計算廣義應變,然後由於差異冷卻、差異收縮與配向性影響,將應變分解成幾部分,最後將修改的應變轉換回對應廣義力。然後執行單獨的應力分析,以取得每個影響的翹曲結果。計算的相關方程式總結如下。
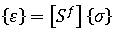
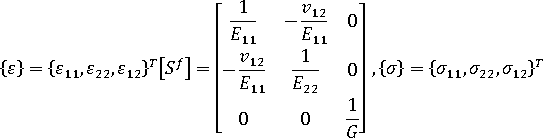
或者,您也可以使用勁度矩陣的形式來寫出虎克定律,如下所示:
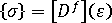
其中
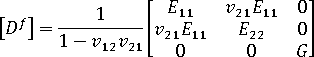
在給定材料配向角度 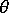 的情況下,我們會將柔度矩陣與勁度矩陣從配向系統轉換為局部元素系統。
的情況下,我們會將柔度矩陣與勁度矩陣從配向系統轉換為局部元素系統。
可透過以下方程式計算廣義應變:
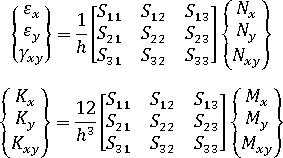
其中,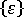 與
與  分別為應變向量與曲率向量。
分別為應變向量與曲率向量。
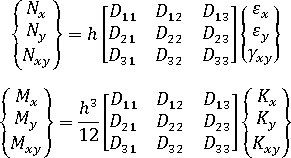
若要隔離翹曲的影響,我們可以使用分解的分量取代 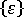 與
與  ,然後重新計算薄膜力與彎矩,並在結構分析中使用新值。
,然後重新計算薄膜力與彎矩,並在結構分析中使用新值。